stringtranslate.com

Acorde menor

En teoría musical , un acorde menor es un acorde que tiene una raíz , una tercera menor y una quinta perfecta . [2] Cuando un acorde comprende solo estas tres notas, se denomina tríada menor . Por ejemplo, la tríada menor construida sobre la, llamada tríada de la menor, tiene tonos la–do–mi:

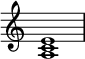
{ \omit Puntuación.TimeSignature \relative c' { <ac e>1 } }
Una tríada menor tiene una tercera menor (m3) en la parte inferior, una tercera mayor (M3) en la parte superior y una quinta perfecta (P5) entre las notas externas.

En el análisis armónico y en las hojas de notas principales , un acorde de Do menor se puede escribir como Cm, C−, Cmin o simplemente la "c" minúscula. Una tríada menor se representa con la notación entera {0, 3, 7}.

Una tríada menor también se puede describir por sus intervalos : el intervalo entre las notas inferior y media es una tercera menor, y el intervalo entre las notas media y superior es una tercera mayor . Por el contrario, una tríada mayor tiene una tercera mayor en la parte inferior y una tercera menor en la superior. Ambas contienen quintas, porque una tercera menor (tres semitonos) más una tercera mayor (cuatro semitonos) es igual a una quinta perfecta (siete semitonos). Los acordes que se construyen con terceras consecutivas (o "apiladas") se denominan tercianas .

En la música clásica occidental de 1600 a 1820 y en la música pop , folk y rock occidental , un acorde mayor se suele tocar como una tríada. Junto con la tríada mayor, la tríada menor es uno de los componentes básicos de la música tonal y del período de práctica común . En la música occidental, un acorde menor, en comparación, "suena más oscuro que un acorde mayor" [3] pero todavía se considera altamente consonante , estable o que no requiere resolución .

Algunos acordes menores con notas adicionales, como el acorde de séptima menor , también pueden llamarse acordes menores.

Consonancia acústica del acorde menor

Una particularidad única del acorde menor es que se trata del único acorde de tres notas en el que las tres notas tienen un armónico, audible y de fila no demasiado alta, en común (más o menos exactamente, según el sistema de afinación utilizado). Este armónico, común a las tres notas, está situado 2 octavas por encima de la nota alta del acorde. Se trata del sexto armónico de la fundamental del acorde, el quinto de la nota media y el cuarto de la nota alta:

En el ejemplo C, E ♭ , G, el armónico común es un G 2 octavas arriba.

Demostración:

Solo entonación

Ilustración de la serie armónica como notación musical. Los números sobre el armónico indican la cantidad de centésimas que se desvía del temperamento igual . Las notas rojas son sostenidas. Las notas azules son bemoles.

En la entonación justa , un acorde menor se afina a menudo (pero no exclusivamente) en la relación de frecuencia 10:12:15 ( tocar ⓘ ). [4] Esta es la primera aparición de una tríada menor en la serie armónica (si está en C: E–G–B). [5] Esto se puede encontrar en iii, vi, ♭ vi, ♭ iii y vii. [6]

En el temperamento igual de doce tonos (ahora el sistema de afinación más común en Occidente), un acorde menor tiene 3 semitonos entre la raíz y la tercera, 4 entre la tercera y la quinta, y 7 entre la raíz y la quinta. Se representa con la notación entera 0,3,7. La quinta del 12-TET (700 cents ) es solo dos cents más estrecha que la quinta justa (3:2, 701,9 cents), pero la tercera menor del 12-TET (300 cents) es notablemente (alrededor de 16 cents) más estrecha que la tercera menor justa (6:5, 315,6 cents). La tercera menor del 12-TET (300 cents) se aproxima más a la tercera menor del límite de 19 ( Limit (música) ) 16:19 Play ⓘ (297,5 cents, el decimonoveno armónico ) con solo 2 cents de error. [7]

Ellis propone que el conflicto entre matemáticos y físicos por un lado y músicos practicantes por el otro con respecto a la supuesta inferioridad del acorde menor y la escala con respecto al mayor puede explicarse debido a la comparación de los físicos entre tríadas menores y mayores, en cuyo caso la menor sale perdiendo, versus la comparación de los músicos entre tríadas de temperamento igual, en cuyo caso la menor sale ganadora ya que la tercera mayor ET está 14 centavos sostenida respecto de la tercera mayor justa, mientras que la tercera menor ET se aproxima mucho a la tercera menor consonante 19:16, que muchos encuentran agradable. [8] [ cita completa necesaria ]

En los siglos XVI al XVIII, antes del 12-TET, la tercera menor en temperamento mediotono era de 310 cents Play ⓘ y mucho más áspera que la tercera menor ET de 300 cents. Otras afinaciones de acordes menores incluyen la tríada supertónica en entonación justa (27:32:40) [4] la tríada menor falsa , [9] Play ⓘ , 16:19:24 [10] Play ⓘ , 12:14:18 (6:7:9) [11] [12] Play ⓘ ( tercera menor septimal ) y la tríada menor pitagórica [10] (54:64:81) Play ⓘ . También hay más afinaciones del acorde menor disponibles en varios temperamentos iguales distintos del 12-TET.

En lugar de hacerlo directamente de la serie armónica , Sorge derivó el acorde menor a partir de la unión de dos tríadas mayores; por ejemplo, la tríada de La menor es la confluencia de las tríadas de Fa y Do mayores. [13] La–Do–Mi = Fa –La–Do–Mi –Sol . Dadas tríadas mayores correctamente afinadas, esto produce una tríada menor correctamente afinada: 10:12:15 en 8:5.

Tabla de acordes menores

Véase también

Referencias

  1. ^ Shirlaw, Matthew (16 de junio de 2015). La teoría de la armonía . p. 81. ISBN 978-1-4510-1534-8. 20:24:30
  2. ^ Miller, Michael (2005). Guía completa para idiotas sobre teoría musical (2.ª ed.). Indianápolis: Alpha. pág. 114. ISBN 1-59257-437-8.
  3. ^ Kamien, Roger (2008). Música: una apreciación (6.ª edición breve). Pág. 46. ISBN 978-0-07-340134-8.
  4. ^ ab Johnston, Ben; Gilmore, Bob (2006) [2003]. "Un sistema de notación para la entonación justa extendida". "Claridad máxima" y otros escritos sobre música . p. 78. ISBN 978-0-252-03098-7. Re, Fa, La (10/9–4/3–5/3)
  5. ^ Hauptmann, Moritz (1888). La naturaleza de la armonía y la métrica. Swan Sonnenschein. pag. 15.
  6. ^ Wright, David (2009). Matemáticas y música . Págs. 140-141. ISBN. 978-0-8218-4873-9.
  7. ^ Helmholtz, Hermann (1954). Sobre las sensaciones del tono como base fisiológica de la teoría de la música . Traducido por Ellis, Alexander J. Nueva York: Dover Publications. pág. 455.
  8. ^ Ellis (1954), pág. 298.
  9. ^ Shirlaw, Matthew (16 de junio de 2015). La teoría de la armonía . p. 375. ISBN 978-1-4510-1534-8.
  10. ^ ab Ruland, Heiner (1992). Ampliando la conciencia tonal . pag. 39.ISBN​ 978-1-85584-170-3.
  11. ^ Helmholtz, Hermann (1885). Sobre las sensaciones del sonido como base fisiológica para la teoría de la música. Longmans, Green. pág. 468.
  12. ^ Mathews, William Smythe Babcock (1805). Música: una revista mensual dedicada al arte, la ciencia, la técnica y la literatura de la música . 7 : 608. Los tonos re, fa y la, tal como se dan en el acordeón, vibracionalmente son 6:7:9. No se trata de una tríada menor, ni nada que se le parezca, aunque su quinta es exactamente la misma que en la menor y la mayor, y la proporción 6:9 es simplemente 2:3. {{cite journal}}: Falta o está vacío |title=( ayuda )
  13. ^ Lester, Joel (1994). Teoría de la composición en el siglo XVIII . pág. 194. ISBN 978-0-674-15523-7.

Enlaces externos