En matemáticas , la teoría de catástrofes es una rama de la teoría de la bifurcación en el estudio de sistemas dinámicos ; también es un caso especial particular de la teoría de la singularidad más general en geometría .
La teoría de la bifurcación estudia y clasifica fenómenos caracterizados por cambios repentinos en el comportamiento que surgen de pequeños cambios en las circunstancias, analizando cómo la naturaleza cualitativa de las soluciones de las ecuaciones depende de los parámetros que aparecen en la ecuación. Esto puede provocar cambios repentinos y dramáticos, por ejemplo, el momento y la magnitud impredecibles de un deslizamiento de tierra .
La teoría de la catástrofe se originó con el trabajo del matemático francés René Thom en la década de 1960 y se hizo muy popular gracias a los esfuerzos de Christopher Zeeman en la década de 1970. Considera el caso especial en el que el equilibrio estable de largo plazo puede identificarse como el mínimo de una función potencial suave y bien definida ( función de Lyapunov ). Pequeños cambios en ciertos parámetros de un sistema no lineal pueden hacer que aparezcan o desaparezcan equilibrios, o que pasen de atraer a repeler y viceversa, lo que lleva a cambios grandes y repentinos en el comportamiento del sistema. Sin embargo, examinada en un espacio de parámetros más amplio , la teoría de la catástrofe revela que tales puntos de bifurcación tienden a ocurrir como parte de estructuras geométricas cualitativas bien definidas.
A finales de la década de 1970, las aplicaciones de la teoría de la catástrofe a áreas fuera de su alcance comenzaron a ser criticadas, especialmente en biología y ciencias sociales. [1] [2] Zahler y Sussmann, en un artículo de 1977 en Nature , se refirieron a tales aplicaciones como "caracterizadas por razonamientos incorrectos, suposiciones inverosímiles, consecuencias erróneas y afirmaciones exageradas". [3] Como resultado, la teoría de la catástrofe se ha vuelto menos popular en sus aplicaciones. [4]
La teoría de catástrofes analiza puntos críticos degenerados de la función potencial, puntos donde no sólo la primera derivada, sino una o más derivadas superiores de la función potencial también son cero. Estos son los llamados gérmenes de las geometrías de catástrofe. La degeneración de estos puntos críticos se puede desarrollar expandiendo la función potencial como una serie de Taylor en pequeñas perturbaciones de los parámetros.
Cuando los puntos degenerados no son meramente accidentales, sino estructuralmente estables , existen como centros organizadores de estructuras geométricas particulares de menor degeneración, con características críticas en el espacio de parámetros que los rodea. Si la función potencial depende de dos o menos variables activas y de cuatro o menos parámetros activos, entonces sólo hay siete estructuras genéricas para estas geometrías de bifurcación, con las correspondientes formas estándar en las que la serie de Taylor alrededor de los gérmenes de la catástrofe puede transformarse mediante difeomorfismo ( una transformación suave cuya inversa también lo es). [ cita necesaria ] Estos siete tipos fundamentales ahora se presentan, con los nombres que Thom les dio.
La teoría de catástrofes estudia sistemas dinámicos que describen la evolución [5] de una variable de estado a lo largo del tiempo :
En la ecuación anterior, se denomina función potencial y, a menudo, es un vector o un escalar que parametriza la función potencial. El valor de puede cambiar con el tiempo y también puede denominarse variable de control . En los siguientes ejemplos, parámetros como son dichos controles.


Cuando a < 0 , el potencial V tiene dos extremos: uno estable y otro inestable. Si el parámetro a aumenta lentamente, el sistema puede seguir el punto mínimo estable. Pero en a = 0 los extremos estable e inestable se encuentran y se aniquilan. Este es el punto de bifurcación. En a > 0 ya no hay una solución estable. Si se sigue un sistema físico a través de una bifurcación, se encuentra que cuando a llega a 0, la estabilidad de la solución a < 0 se pierde repentinamente y el sistema hará una transición repentina a un comportamiento nuevo y muy diferente. Este valor de bifurcación del parámetro a a veces se denomina " punto de inflexión ".
La geometría de la cúspide es muy común cuando se explora lo que sucede con una bifurcación de pliegue si se agrega un segundo parámetro, b , al espacio de control. Al variar los parámetros, se encuentra que ahora hay una curva (azul) de puntos en el espacio ( a , b ) donde se pierde la estabilidad, donde la solución estable saltará repentinamente a un resultado alternativo.
Pero en una geometría de cúspide, la curva de bifurcación vuelve sobre sí misma, dando una segunda rama donde esta solución alternativa pierde estabilidad y dará un salto de regreso al conjunto de soluciones original. Por lo tanto, al aumentar b repetidamente y luego disminuirlo, se pueden observar bucles de histéresis , ya que el sistema alternativamente sigue una solución, salta a la otra, sigue a la otra hacia atrás y luego salta de regreso a la primera.
Sin embargo, esto sólo es posible en la región del espacio de parámetros a < 0 . A medida que a aumenta, los bucles de histéresis se vuelven cada vez más pequeños, hasta que por encima de a = 0 desaparecen por completo (la catástrofe de la cúspide) y solo hay una solución estable.
También se puede considerar lo que sucede si se mantiene b constante y se varía a . En el caso simétrico b = 0 , se observa una bifurcación en forma de horquilla a medida que a se reduce, con una solución estable dividiéndose repentinamente en dos soluciones estables y una solución inestable a medida que el sistema físico pasa a a < 0 a través del punto de cúspide (0,0). (un ejemplo de ruptura espontánea de simetría ). Lejos del punto de la cúspide, no hay ningún cambio repentino en la solución física que se sigue: al pasar por la curva de bifurcaciones de pliegue, todo lo que sucede es que queda disponible una segunda solución alternativa.
Una sugerencia famosa es que la catástrofe de la cúspide puede usarse para modelar el comportamiento de un perro estresado, que puede responder acobardándose o enojándose. [6] La sugerencia es que en un estrés moderado ( a > 0 ), el perro exhibirá una transición suave de respuesta de intimidado a enojado, dependiendo de cómo se le provoque. Pero los niveles de estrés más altos corresponden a moverse a la región ( a < 0 ). Luego, si el perro comienza a acobardarse, seguirá acobardado a medida que se irrita cada vez más, hasta que alcanza el punto de "pliegue", cuando de repente y de forma discontinua pasará al modo de enfado. Una vez en modo 'enojado', seguirá enfadado, incluso si el parámetro de irritación directa se reduce considerablemente.
Un sistema mecánico simple, la "Máquina de Catástrofe Zeeman", ilustra muy bien una catástrofe culminante. En este dispositivo, variaciones suaves en la posición del extremo de un resorte pueden provocar cambios repentinos en la posición de rotación de una rueda adjunta. [7]
La falla catastrófica de un sistema complejo con redundancia paralela se puede evaluar basándose en la relación entre las tensiones locales y externas. El modelo de la mecánica de fractura estructural es similar al comportamiento de catástrofe de la cúspide. El modelo predice la capacidad de reserva de un sistema complejo.
Otras aplicaciones incluyen la transferencia de electrones en la esfera exterior que se encuentra con frecuencia en sistemas químicos y biológicos, [8] modelando la dinámica de los núcleos de condensación de nubes en la atmósfera, [9] y modelando precios inmobiliarios. [10]
Las bifurcaciones de los pliegues y la geometría de las cúspides son, con diferencia, las consecuencias prácticas más importantes de la teoría de la catástrofe. Son patrones que se repiten una y otra vez en la física, la ingeniería y la modelización matemática. Producen fuertes eventos de lentes gravitacionales y proporcionan a los astrónomos uno de los métodos utilizados para detectar los agujeros negros y la materia oscura del universo, a través del fenómeno de lentes gravitacionales que producen múltiples imágenes de quásares distantes . [11]
Las geometrías de catástrofes simples restantes son muy especializadas en comparación y se presentan aquí sólo por curiosidad.


El espacio de parámetros de control es tridimensional. La bifurcación establecida en el espacio de parámetros se compone de tres superficies de bifurcaciones de pliegue, que se encuentran en dos líneas de bifurcaciones de cúspides, que a su vez se encuentran en un único punto de bifurcación de cola de golondrina.
A medida que los parámetros atraviesan la superficie de las bifurcaciones de los pliegues, desaparecen un mínimo y un máximo de la función potencial. En las bifurcaciones de las cúspides, dos mínimos y un máximo se reemplazan por un mínimo; más allá de ellos, las bifurcaciones de los pliegues desaparecen. En el punto de cola de golondrina, dos mínimos y dos máximos se encuentran en un único valor de x . Para valores de a > 0 , más allá de la cola de golondrina, hay un par máximo-mínimo o ninguno, dependiendo de los valores de b y c . Por lo tanto, dos de las superficies de las bifurcaciones de los pliegues y las dos líneas de bifurcaciones de las cúspides donde se encuentran para a < 0 desaparecen en el punto de la cola de golondrina, para ser reemplazadas por una única superficie de las bifurcaciones de los pliegues restante. El último cuadro de Salvador Dalí , La cola de golondrina , se basó en esta catástrofe.

Dependiendo de los valores de los parámetros, la función potencial puede tener tres, dos o un mínimo local diferente, separados por los lugares de las bifurcaciones de los pliegues. En la punta de mariposa, las diferentes 3 superficies de bifurcaciones de pliegue, las 2 superficies de bifurcaciones de cúspides y las líneas de bifurcaciones de cola de golondrina se encuentran y desaparecen, dejando una sola estructura de cúspide cuando a > 0 .


Las catástrofes umbilicales son ejemplos de catástrofes de rango 2. Se pueden observar en óptica en las superficies focales creadas por la luz que se refleja en una superficie en tres dimensiones y están íntimamente relacionados con la geometría de superficies casi esféricas: el punto umbilical . Thom propuso que la catástrofe umbilical hiperbólica modelaba la ruptura de una ola y la catástrofe umbilical elíptica modelaba la creación de estructuras parecidas a pelos.
Vladimir Arnold dio a las catástrofes la clasificación ADE , debido a una profunda conexión con simples grupos de Lie . [ cita necesaria ]
Hay objetos en la teoría de la singularidad que corresponden a la mayoría de los otros grupos de Lie simples.

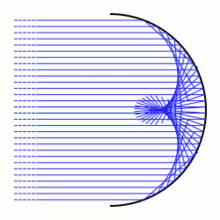
Como predice la teoría de la catástrofe, las singularidades son genéricas y estables bajo perturbación. Esto explica cómo las líneas y superficies brillantes son estables bajo perturbación. Las sustancias cáusticas que se ven en el fondo de una piscina, por ejemplo, tienen una textura distintiva y sólo presentan unos pocos tipos de puntos singulares, aunque la superficie del agua esté en constante cambio. [12]
El borde del arcoíris , por ejemplo, tiene un pliegue catastrófico. Debido a la naturaleza ondulatoria de la luz, la catástrofe tiene finos detalles de difracción descritos por la función de Airy . Este es un resultado genérico y no depende de la forma precisa de la gota de agua, por lo que el borde del arco iris siempre tiene la forma de una función Airy. [13] [14] La misma catástrofe de la función de Airy se puede ver en la dispersión nuclear-nuclear ("arco iris nuclear"). [15]
La catástrofe cúspide es la siguiente más sencilla de observar. Debido a la naturaleza ondulatoria de la luz, la catástrofe tiene finos detalles de difracción descritos por la función de Pearcey . [16] También se han observado catástrofes de orden superior, como la cola de golondrina y la mariposa. [17]