
En física , la ruptura de simetría es un fenómeno en el que un estado desordenado pero simétrico colapsa en un estado ordenado, pero menos simétrico. [1] Este colapso es a menudo una de las muchas bifurcaciones posibles que puede tener una partícula a medida que se acerca a un estado de menor energía. Debido a las muchas posibilidades, un observador puede asumir que el resultado del colapso es arbitrario. Este fenómeno es fundamental para la teoría cuántica de campos (QFT) y, además, para la comprensión contemporánea de la física . [2] Específicamente, juega un papel central en el modelo de Glashow-Weinberg-Salam que forma parte del modelo estándar que modela el sector electrodébil.

En un sistema infinito ( espacio-tiempo de Minkowski ) ocurre una ruptura de simetría, sin embargo en un sistema finito (es decir, cualquier sistema supercondensado real), el sistema es menos predecible, pero en muchos casos ocurre un efecto túnel cuántico . [2] [3] La ruptura de simetría y el efecto túnel se relacionan a través del colapso de una partícula en un estado no simétrico mientras busca una energía más baja. [4]
La ruptura de simetría se puede distinguir en dos tipos, explícita y espontánea . Se caracterizan por si las ecuaciones de movimiento no son invariantes o si el estado fundamental no es invariante.
En esta sección se describe la ruptura espontánea de la simetría. Se trata de la idea de que, para un sistema físico, la configuración de energía más baja (el estado de vacío ) no es la configuración más simétrica del sistema. En términos generales, existen tres tipos de simetría que se pueden romper: discreta, continua y de calibración, ordenadas en orden creciente de tecnicismo.
Un ejemplo de un sistema con simetría discreta se da en la figura con el gráfico rojo: considere una partícula que se mueve en este gráfico, sujeta a la gravedad . Un gráfico similar podría darse por la función . Este sistema es simétrico bajo reflexión en el eje y. Hay tres posibles estados estacionarios para la partícula: la cima de la colina en , o la parte inferior, en . Cuando la partícula está en la cima, la configuración respeta la simetría de reflexión: la partícula permanece en el mismo lugar cuando se refleja. Sin embargo, las configuraciones de energía más bajas son aquellas en . Cuando la partícula está en cualquiera de estas configuraciones, ya no está fija bajo reflexión en el eje y: la reflexión intercambia los dos estados de vacío.
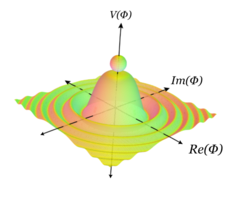
Un ejemplo con simetría continua se da mediante un análogo 3d del ejemplo anterior, de rotar el gráfico alrededor de un eje a través de la parte superior de la colina, o equivalentemente dado por el gráfico . Este es esencialmente el gráfico del potencial del sombrero mexicano . Este tiene una simetría continua dada por la rotación sobre el eje a través de la parte superior de la colina (así como una simetría discreta por reflexión a través de cualquier plano radial). Nuevamente, si la partícula está en la parte superior de la colina, está fija bajo rotaciones, pero tiene mayor energía gravitacional en la parte superior. En la parte inferior, ya no es invariante bajo rotaciones, sino que minimiza su energía potencial gravitacional. Además, las rotaciones mueven la partícula de una configuración de minimización de energía a otra. Aquí hay una novedad que no se vio en el ejemplo anterior: desde cualquiera de los estados de vacío es posible acceder a cualquier otro estado de vacío con solo una pequeña cantidad de energía, moviéndose alrededor del canal en la parte inferior de la colina, mientras que en el ejemplo anterior, para acceder al otro vacío, la partícula tendría que cruzar la colina, lo que requiere una gran cantidad de energía.
La ruptura de la simetría de gauge es la más sutil, pero tiene consecuencias físicas importantes. En términos generales, para los fines de esta sección, una simetría de gauge es una asignación de sistemas con simetría continua a cada punto del espacio-tiempo . La simetría de gauge prohíbe la generación de masa para los campos de gauge , pero se han observado campos de gauge masivos ( bosones W y Z ). La ruptura espontánea de la simetría se desarrolló para resolver esta inconsistencia. La idea es que en una etapa temprana del universo estaba en un estado de alta energía, análogo a la partícula que está en la cima de la colina, y por lo tanto tenía simetría de gauge completa y todos los campos de gauge no tenían masa. A medida que se enfrió, se asentó en una elección de vacío, rompiendo así espontáneamente la simetría, eliminando así la simetría de gauge y permitiendo la generación de masa de esos campos de gauge. Una explicación completa es altamente técnica: vea interacción electrodébil .
En la ruptura espontánea de simetría (SSB), las ecuaciones de movimiento del sistema son invariantes, pero cualquier estado de vacío (estado de menor energía) no lo es.
Por ejemplo, si hay un átomo con dos estados de vacío, al ocupar cualquiera de estos estados se rompe la simetría doble. Este acto de seleccionar uno de los estados cuando el sistema alcanza una energía menor se denomina SSB. Cuando esto sucede, el átomo ya no es simétrico (simetría reflexiva) y ha colapsado en un estado de energía menor.
Este tipo de ruptura de simetría está parametrizada por un parámetro de orden . Un caso especial de este tipo de ruptura de simetría es la ruptura de simetría dinámica .
En el contexto lagrangiano de la teoría cuántica de campos (QFT), el lagrangiano es una función de los campos cuánticos que es invariante bajo la acción de un grupo de simetría . Sin embargo, el valor esperado del vacío formado cuando la partícula colapsa a una energía menor puede no ser invariante bajo . En este caso, romperá parcialmente la simetría de , en un subgrupo . Esta es una ruptura espontánea de la simetría.
Sin embargo, en el contexto de la simetría de calibre, la SSB es el fenómeno por el cual los campos de calibre "adquieren masa" a pesar de que la invariancia de calibre impone que dichos campos no tengan masa. Esto se debe a que la SSB de la simetría de calibre rompe la invariancia de calibre, y tal ruptura permite la existencia de campos de calibre masivos. Esta es una exención importante del Teorema de Goldstone , donde un Bosón de Nambu-Goldstone puede ganar masa, convirtiéndose en un Bosón de Higgs en el proceso. [5]
Además, en este contexto, el uso de "ruptura de simetría", si bien es un término estándar, es un nombre inapropiado, ya que la "simetría" de calibración no es realmente una simetría sino una redundancia en la descripción del sistema. Matemáticamente, esta redundancia es una elección de trivialización , algo análoga a la redundancia que surge de una elección de base.
La ruptura espontánea de la simetría también está asociada a las transiciones de fase . Por ejemplo, en el modelo de Ising , cuando la temperatura del sistema cae por debajo de la temperatura crítica, se rompe la simetría del vacío, lo que da lugar a una transición de fase del sistema.

En la ruptura explícita de simetría (ESB), las ecuaciones de movimiento que describen un sistema son variantes en virtud de la ruptura de simetría. En la mecánica hamiltoniana o mecánica lagrangiana , esto sucede cuando hay al menos un término en el hamiltoniano (o lagrangiano) que rompe explícitamente la simetría dada.
En el contexto hamiltoniano, esto se estudia a menudo cuando el hamiltoniano se puede escribir .
He aquí un "hamiltoniano de base" que tiene cierta simetría manifiesta. Más explícitamente, es simétrico bajo la acción de un grupo (de Lie) . A menudo, se trata de un hamiltoniano integrable.
El es un hamiltoniano de perturbación o interacción. No es invariante bajo la acción de . Suele ser proporcional a un pequeño parámetro perturbativo.
Éste es, en esencia, el paradigma de la teoría de perturbaciones en mecánica cuántica. Un ejemplo de su uso es el hallazgo de la estructura fina de los espectros atómicos.
La ruptura de simetría puede cubrir cualquiera de los siguientes escenarios:
Uno de los primeros casos de simetría rota discutidos en la literatura de física está relacionado con la forma que adopta un cuerpo de fluido incompresible en rotación uniforme en equilibrio gravitacional e hidrostático . Jacobi [6] y poco después Liouville [7] en 1834, discutieron el hecho de que un elipsoide triaxial era una solución de equilibrio para este problema cuando la energía cinética comparada con la energía gravitacional del cuerpo en rotación excedía un cierto valor crítico. La simetría axial presentada por los esferoides de McLaurin se rompe en este punto de bifurcación. Además, por encima de este punto de bifurcación, y para momento angular constante, las soluciones que minimizan la energía cinética son los elipsoides de Jacobi no axialmente simétricos en lugar de los esferoides de Maclaurin .