El radio de Einstein es el radio de un anillo de Einstein y es un ángulo característico del efecto de lente gravitacional en general, ya que las distancias típicas entre imágenes en el efecto de lente gravitacional son del orden del radio de Einstein. [1]
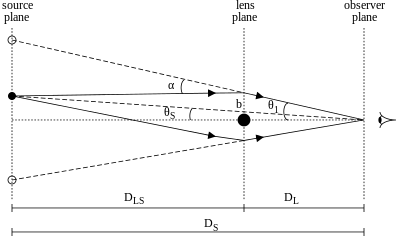
En la siguiente derivación del radio de Einstein, asumiremos que toda la masa M de la galaxia con efecto lente L está concentrada en el centro de la galaxia.
Para una masa puntual, la desviación se puede calcular y es una de las pruebas clásicas de la relatividad general . Para ángulos pequeños α 1, la desviación total por una masa puntual M se da (véase la métrica de Schwarzschild ) por
dónde
Al observar que, para ángulos pequeños y con el ángulo expresado en radianes , el punto de aproximación más cercano b 1 en un ángulo θ 1 para la lente L en una distancia D L está dado por b 1 = θ 1 D L , podemos reexpresar el ángulo de flexión α 1 como
Si fijamos θ S como el ángulo en el que se vería la fuente sin la lente (que generalmente no es observable), y θ 1 como el ángulo observado de la imagen de la fuente con respecto a la lente, entonces se puede ver a partir de la geometría del efecto lente (contando distancias en el plano de la fuente) que la distancia vertical abarcada por el ángulo θ 1 a una distancia D S es la misma que la suma de las dos distancias verticales θ S D S y α 1 D LS . Esto da la ecuación de la lente
que se puede reorganizar para dar
Al igualar (ecuación 1) a (ecuación 2) y reorganizar, obtenemos
Para una fuente justo detrás de la lente, θ S = 0 , la ecuación de la lente para una masa puntual da un valor característico para θ 1 que se llama ángulo de Einstein , denotado θ E . Cuando θ E se expresa en radianes y la fuente de lente está suficientemente lejos, el radio de Einstein , denotado R E , se da por
Poniendo θ S = 0 y resolviendo θ 1 obtenemos
El ángulo de Einstein para una masa puntual proporciona una escala lineal conveniente para crear variables de lente adimensionales. En términos del ángulo de Einstein, la ecuación de lente para una masa puntual se convierte en
Sustituyendo las constantes se obtiene
En la última forma, la masa se expresa en masas solares ( M ☉ y las distancias en Giga parsec (Gpc). El radio de Einstein es más prominente para una lente que normalmente se encuentra a mitad de camino entre la fuente y el observador.
Para un cúmulo denso con masa M c ≈10 × 10 15 M ☉ a una distancia de 1 Gigaparsec (1 Gpc) este radio podría ser tan grande como 100 arcsec (llamado macrolente ). Para un evento de microlente gravitacional (con masas del orden de1 M ☉ ) buscar a distancias galácticas (digamos D ~3 kpc ), el radio típico de Einstein sería del orden de milisegundos de arco. En consecuencia, es imposible observar imágenes separadas en eventos de microlente con las técnicas actuales.
De la misma manera, para el rayo de luz inferior que llega al observador desde debajo de la lente, tenemos
y
y por lo tanto
El argumento anterior se puede extender para lentes que tienen una masa distribuida, en lugar de una masa puntual, utilizando una expresión diferente para el ángulo de curvatura α; entonces se pueden calcular las posiciones θ I ( θ S ) de las imágenes. Para pequeñas desviaciones, este mapeo es uno a uno y consiste en distorsiones de las posiciones observadas que son invertibles. Esto se llama efecto de lente débil . Para grandes desviaciones, se pueden tener múltiples imágenes y un mapeo no invertible: esto se llama efecto de lente fuerte . Tenga en cuenta que para que una masa distribuida resulte en un anillo de Einstein, debe ser axialmente simétrico.