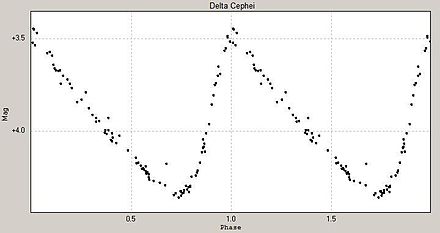
Las pulsaciones estelares son causadas por expansiones y contracciones en las capas externas cuando una estrella busca mantener el equilibrio . Estas fluctuaciones en el radio estelar provocan cambios correspondientes en la luminosidad de la estrella . Los astrónomos pueden deducir este mecanismo midiendo el espectro y observando el efecto Doppler . [1] Muchas estrellas variables intrínsecas que pulsan con grandes amplitudes , como las cefeidas clásicas , las estrellas RR Lyrae y las estrellas Delta Scuti de gran amplitud, muestran curvas de luz regulares .
Este comportamiento regular contrasta con la variabilidad de las estrellas que se encuentran paralelas y al lado de alta luminosidad/baja temperatura de las estrellas variables clásicas en el diagrama de Hertzsprung-Russell . Se observa que estas estrellas gigantes sufren pulsaciones que van desde una débil irregularidad, cuando todavía se puede definir un tiempo o período de ciclo promedio (como en la mayoría de RV Tauri y variables semirregulares ) hasta la casi ausencia de repetitividad en las variables irregulares . Las variables de W Virginis están en la interfaz; las de período corto son regulares y las de período más largo muestran primero alternancias relativamente regulares en los ciclos de pulsaciones, seguidas por la aparición de leves irregularidades como en las estrellas RV Tauri en las que se transforman gradualmente a medida que sus períodos se alargan. [2] [3] Las teorías de evolución estelar y pulsación sugieren que estas estrellas irregulares tienen una relación luminosidad/masa (L/M) mucho mayor.
Muchas estrellas son pulsadores no radiales, que tienen fluctuaciones de brillo más pequeñas que las de las variables regulares utilizadas como velas estándar. [4] [5]
Un requisito previo para la variabilidad irregular es que la estrella pueda cambiar su amplitud en la escala de tiempo de un período. En otras palabras, el acoplamiento entre pulsación y flujo de calor debe ser suficientemente grande para permitir tales cambios. Este acoplamiento se mide por la tasa relativa de crecimiento o disminución lineal κ ( kappa ) de la amplitud de un modo normal dado en un ciclo de pulsación (período). Para las variables regulares (Cefeidas, RR Lyrae, etc.), el modelado estelar numérico y el análisis de estabilidad lineal muestran que κ es como máximo del orden de un par de porcentajes para los modos de pulsación excitados relevantes. Por otro lado, el mismo tipo de análisis muestra que para los modelos L/M altos κ es considerablemente mayor (30% o más).
Para las variables regulares, las pequeñas tasas de crecimiento relativo κ implican que hay dos escalas de tiempo distintas, a saber, el período de oscilación y el tiempo más largo asociado con la variación de amplitud. Matemáticamente hablando, la dinámica tiene una variedad central , o más precisamente una variedad central cercana. Además, se ha descubierto que las pulsaciones estelares sólo son débilmente no lineales, en el sentido de que su descripción puede limitarse a la potencia de las amplitudes de las pulsaciones. Estas dos propiedades son muy generales y ocurren para sistemas oscilatorios en muchos otros campos como la dinámica de poblaciones , la oceanografía , la física del plasma , etc.
La débil no linealidad y la larga escala de tiempo de la variación de amplitud permiten simplificar la descripción temporal del sistema pulsante a la de sólo las amplitudes de pulsación, eliminando así el movimiento en la corta escala de tiempo del período. El resultado es una descripción del sistema en términos de ecuaciones de amplitud que se truncan a potencias bajas de las amplitudes. Estas ecuaciones de amplitud se han obtenido mediante una variedad de técnicas, por ejemplo, el método de eliminación de términos seculares de Poincaré-Lindstedt, o el método de perturbación asintótica multitiempo, [6] [7] [8] y, más en general, la teoría de la forma normal. [9] [10] [11]
Por ejemplo, en el caso de dos modos no resonantes, situación que se encuentra generalmente en las variables de RR Lyrae, la evolución temporal de las amplitudes A 1 y A 2 de los dos modos normales 1 y 2 se rige por el siguiente conjunto de diferenciales ordinarios. ecuaciones
Estas ecuaciones de amplitud se han limitado a las no linealidades no triviales de orden más bajo. Las soluciones de interés en la teoría de la pulsación estelar son las soluciones asintóticas (ya que el tiempo tiende al infinito) porque la escala de tiempo para las variaciones de amplitud es generalmente muy corta en comparación con la escala de tiempo de evolución de la estrella, que es la escala de tiempo de combustión nuclear. Las ecuaciones anteriores tienen soluciones de punto fijo con amplitudes constantes, correspondientes a monomodo (A 1 0, A 2 = 0) o (A 1 = 0, A 2 0) y bimodo (A 1 0, A 2 0). soluciones. Estos corresponden a pulsaciones de la estrella de una o dos veces. Es importante enfatizar que no existe otra solución asintótica de las ecuaciones anteriores para coeficientes de acoplamiento físicos (es decir, negativos).
Para los modos resonantes , las ecuaciones de amplitud apropiadas tienen términos adicionales que describen el acoplamiento resonante entre los modos. La progresión de Hertzsprung en la morfología de la curva de luz de las cefeidas clásicas (simplemente periódicas) es el resultado de una conocida resonancia 2:1 entre el modo de pulsación fundamental y el segundo modo de sobretono . [14] La ecuación de amplitud se puede ampliar aún más a pulsaciones estelares no radiales. [15] [16]
En el análisis global de estrellas pulsantes, las ecuaciones de amplitud permiten trazar el diagrama de bifurcación entre posibles estados pulsantes. En esta imagen, los límites de la franja de inestabilidad donde se producen las pulsaciones durante la evolución de la estrella corresponden a una bifurcación de Hopf . [17]
La existencia de una variedad central elimina la posibilidad de pulsaciones caóticas (es decir, irregulares) en la escala de tiempo del período. Aunque las ecuaciones de amplitud resonante son lo suficientemente complejas como para permitir también soluciones caóticas, este es un caos muy diferente porque ocurre en la variación temporal de las amplitudes y ocurre en una escala de tiempo larga.
Si bien es posible un comportamiento irregular a largo plazo en las variaciones temporales de las amplitudes de pulsación cuando se aplican ecuaciones de amplitud, esta no es la situación general. De hecho, para la mayoría de las observaciones y modelos, las pulsaciones de estas estrellas se producen con amplitudes de Fourier constantes, lo que da lugar a pulsaciones regulares que pueden ser periódicas o multiperiódicas (cuasi periódicas en la literatura matemática).
Se sabe desde hace siglos que las curvas de luz de las estrellas variables intrínsecas con grandes amplitudes exhiben un comportamiento que va desde una regularidad extrema, como en el caso de las estrellas Cefeidas clásicas y RR Lyrae , hasta una irregularidad extrema, en el caso de las llamadas variables irregulares . En las estrellas de Población II, esta irregularidad aumenta gradualmente desde las variables del período bajo W Virginis a través de las variables RV Tauri hasta el régimen de las variables semirregulares . El caos de baja dimensión en las pulsaciones estelares es la interpretación actual de este fenómeno establecido.
El comportamiento regular de las Cefeidas ha sido modelado exitosamente con hidrodinámica numérica desde la década de 1960, [18] [19] y desde un punto de vista teórico se entiende fácilmente como debido a la presencia de una variedad central que surge debido a la naturaleza débilmente disipativa. del sistema dinámico . [20] Esto, y el hecho de que las pulsaciones son débilmente no lineales, permite una descripción del sistema en términos de ecuaciones de amplitud [21] [22] y una construcción del diagrama de bifurcación (ver también teoría de la bifurcación ) de los posibles tipos de pulsación (o ciclos límite ), como pulsación de modo fundamental , primera o segunda pulsación de armónico , o pulsaciones de modo doble más complicadas en las que se excitan varios modos con amplitudes constantes. Los límites de la franja de inestabilidad , donde se producen las pulsaciones durante la evolución de la estrella, corresponden a una bifurcación de Hopf .
Por el contrario, la irregularidad de las estrellas de gran amplitud de la Población II es más difícil de explicar. La variación de la amplitud de la pulsación durante un período implica una gran disipación y, por lo tanto, no existe una variedad central. Se han propuesto varios mecanismos, pero faltan. Uno sugiere la presencia de varias frecuencias de pulsación estrechamente espaciadas que chocarían entre sí, pero tales frecuencias no existen en los modelos estelares apropiados. Otra sugerencia más interesante es que las variaciones son de naturaleza estocástica, [23] pero no se ha propuesto ni existe ningún mecanismo que pueda proporcionar la energía para variaciones de amplitud tan grandes observadas. Ahora se ha establecido que el mecanismo detrás de las curvas de luz irregulares es una dinámica caótica subyacente de baja dimensión (ver también Teoría del Caos ). Esta conclusión se basa en dos tipos de estudios.
Los pronósticos numéricos de dinámica de fluidos computacional para las pulsaciones de secuencias de los modelos estelares W Virginis exhiben dos enfoques del comportamiento irregular que son una clara firma del caos de baja dimensión . La primera indicación proviene de los primeros mapas de retorno en los que se traza un radio máximo, o cualquier otra variable adecuada, frente al siguiente. La secuencia de modelos muestra un período que duplica la bifurcación , o cascada, que conduce al caos. La forma casi cuadrática del mapa es indicativa de caos e implica un mapa de herradura subyacente . [24] [25] Otras secuencias de modelos siguen una ruta algo diferente, pero también hacia el caos, a saber, la ruta Pommeau-Manneville o bifurcación tangente . [26] [27]
A continuación se muestra una visualización similar del período de duplicación en cascada hasta el caos para una secuencia de modelos estelares que difieren por su temperatura superficial promedio T. El gráfico muestra tripletas de valores del radio estelar (R i , R i+1 , R i+ 2 ) donde los índices i , i+1 , i+2 indican intervalos de tiempo sucesivos.
La presencia de caos de baja dimensión también se confirma mediante otro análisis más sofisticado de las pulsaciones del modelo que extrae las órbitas periódicas inestables más bajas y examina su organización topológica (torsión). Se encuentra que el atractor subyacente tiene bandas como el atractor de Roessler , pero con un giro adicional en la banda. [28]
El método de reconstrucción de flujo global [29] utiliza una única señal observada {s i } para inferir propiedades del sistema dinámico que la generó. Se construyen los primeros 'vectores' N-dimensionales . El siguiente paso consiste en encontrar una expresión para el operador de evolución no lineal que toma el sistema de vez en cuando , es decir, . El teorema de Takens garantiza que, en circunstancias muy generales, las propiedades topológicas de este operador de evolución reconstruido son las mismas que las del sistema físico, siempre que la dimensión de incrustación N sea lo suficientemente grande. Así, a partir del conocimiento de una única variable observada se pueden inferir propiedades sobre el sistema físico real que está gobernado por varias variables independientes.
Este enfoque se ha aplicado a los datos de AAVSO para la estrella R Scuti [30] [31]. Se podría inferir que las pulsaciones irregulares de esta estrella surgen de una dinámica subyacente de 4 dimensiones. Dicho de otra manera, esto dice que a partir de 4 observaciones vecinas cualesquiera se puede predecir la siguiente. Desde un punto de vista físico dice que existen 4 variables independientes que describen la dinámica del sistema. El método de los falsos vecinos más cercanos corrobora una dimensión de incrustación de 4. La dimensión fractal de la dinámica de R Scuti, como se infiere de los exponentes de Lyapunov calculados , se encuentra entre 3,1 y 3,2.
A partir de un análisis de los puntos fijos del operador de evolución se puede inferir una bonita imagen física, a saber, que las pulsaciones surgen de la excitación de un modo de pulsación inestable que se acopla de forma no lineal a un segundo modo de pulsación estable que está en una resonancia 2:1. con el primero , un escenario descrito por el teorema de Shilnikov. [32]
Este mecanismo de resonancia no se limita a R Scuti, sino que se ha descubierto que es válido para varias otras estrellas para las cuales los datos de observación son suficientemente buenos. [33]
![{\displaystyle {\begin{alineado}{\frac {dA_{1}}{dt}}&=\kappa _{1}A_{1}+\left(Q_{11}A_{1}^{2} +Q_{12}A_{2}^{2}\right)A_{1}\\[1ex]{\frac {dA_{2}}{dt}}&=\kappa _{2}A_{2} +\left(Q_{21}A_{1}^{2}+Q_{22}A_{2}^{2}\right)A_{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5b7094bcd1d64b43b9f30ee44a8467e82f87ac5)
