
El experimento de Pound-Rebka monitoreó los cambios de frecuencia en los rayos gamma a medida que subían y bajaban en el campo gravitatorio de la Tierra. El experimento puso a prueba las predicciones de Albert Einstein de 1907 y 1911, basadas en el principio de equivalencia , de que los fotones ganarían energía al descender un potencial gravitatorio y perderían energía al ascender a través de un potencial gravitatorio. [p 1] [p 2] Fue propuesto por Robert Pound y su estudiante de posgrado Glen A. Rebka Jr. en 1959, [p 3] y fue la última de las pruebas clásicas de la relatividad general en ser verificada. [p 4] La medición del corrimiento al rojo y al azul gravitatorios mediante este experimento validó la predicción del principio de equivalencia de que los relojes deberían medirse como si funcionaran a diferentes velocidades en diferentes lugares de un campo gravitatorio . Se considera que es el experimento que marcó el comienzo de una era de pruebas de precisión de la relatividad general.
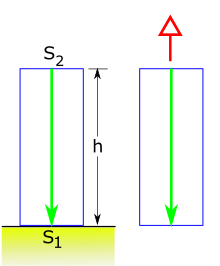
En la década anterior a la publicación de la versión definitiva de la teoría de la relatividad general por parte de Einstein , anticipó varios de los resultados de su teoría final con argumentos heurísticos. Uno de ellos se refería a la luz en un campo gravitatorio. Para demostrar que el principio de equivalencia implica que la luz sufre un desplazamiento Doppler en un campo gravitatorio, Einstein consideró una fuente de luz separada a lo largo del eje z por una distancia por encima de un receptor en un campo gravitatorio homogéneo que tiene una fuerza por unidad de masa de 1 Un haz continuo de energía electromagnética con frecuencia es emitido por hacia Según el principio de equivalencia, este sistema es equivalente a un sistema libre de gravitación que se mueve con aceleración uniforme en la dirección del eje z positivo , con separados por una distancia constante de [p 2]
En el sistema acelerado, la luz emitida desde tarda (en una primera aproximación) en llegar a Pero en este tiempo, la velocidad de habrá aumentado en con respecto a su velocidad cuando se emitió la luz. La frecuencia de la luz que llega a no será, por lo tanto, la frecuencia sino la frecuencia mayor dada por
De acuerdo con el principio de equivalencia, la misma relación se cumple para el sistema no acelerado en un campo gravitacional, donde reemplazamos por la diferencia de potencial gravitacional entre y de modo que [p 2]
En 1916, Einstein utilizó el marco de su recién completada teoría general de la relatividad para actualizar sus argumentos heurísticos anteriores que predecían el corrimiento al rojo gravitacional a una forma más rigurosa. [p 5] El corrimiento al rojo gravitacional y otras dos predicciones de su artículo de 1916, la precesión anómala del perihelio de la órbita de Mercurio y la desviación gravitacional de la luz por el Sol , se han conocido como las "pruebas clásicas" de la relatividad general. La precesión anómala del perihelio de Mercurio había sido reconocida durante mucho tiempo como un problema en la mecánica celeste desde los cálculos de 1859 de Urbain Le Verrier . La observación de la desviación de la luz por el Sol en la expedición Eddington de 1919 catapultó a Einstein a la fama mundial. El corrimiento al rojo gravitacional demostraría ser, con mucho, la más difícil de demostrar de las tres pruebas clásicas.
Los investigadores no se apresuraron a comprobar las predicciones anteriores de Einstein sobre la dilatación gravitacional del tiempo, ya que el efecto previsto era casi inconmensurablemente pequeño. El desplazamiento predicho por Einstein para las líneas espectrales del Sol ascendía a sólo dos partes en un millón, y se enmascararía fácilmente por el ensanchamiento de las líneas debido a la temperatura y la presión, y por la asimetría de las líneas debido al hecho de que las líneas representan la superposición de la absorción de muchas capas turbulentas de la atmósfera solar. [1] Varios intentos de medir el efecto fueron negativos o no concluyentes. La primera afirmación generalmente aceptada de haber medido el corrimiento al rojo gravitacional fue la medición de WS Adams en 1925 de los cambios en las líneas espectrales de la estrella enana blanca Sirio B. [ 2] Sin embargo, incluso las mediciones de Adams han sido puestas en tela de juicio desde entonces por diversas razones. [3]
En la espectroscopia atómica , los fotones visibles y ultravioleta resultantes de las transiciones electrónicas de los electrones de la capa externa, cuando son emitidos por átomos gaseosos en un estado excitado, son absorbidos fácilmente por átomos no excitados de la misma especie. Sin embargo, nunca se había observado una absorbancia correspondiente de los fotones emitidos por los núcleos de los emisores γ porque el retroceso de los núcleos resultó en tanta pérdida de energía por parte de los fotones emitidos que ya no coincidían con los espectros de absorbancia de los núcleos objetivo. En 1958, Rudolf Mössbauer , que estaba analizando la transición de 129 keV del iridio-191, descubrió que al reducir la temperatura del emisor a 90 K, podía lograr una absorbancia resonante. De hecho, las resoluciones de energía que logró fueron de una nitidez inaudita. Había descubierto el fenómeno de la emisión γ sin retroceso . [1] [nota 1]
En 1959, varios grupos de investigación, entre los que destacaban Robert Pound y Glen Rebka en Harvard y un equipo dirigido por John Paul Schiffer en Harwell (Inglaterra), anunciaron planes para explotar este efecto recientemente descubierto para realizar pruebas terrestres del corrimiento al rojo gravitacional.
En febrero de 1960, Schiffer y su equipo fueron los primeros en anunciar el éxito en la medición del corrimiento al rojo gravitacional, pero con un error bastante alto de ±47%. [p 6] Sería la contribución algo posterior de Pound y Rebka en abril de 1960, que utilizó una fuente de radiación más fuerte, una longitud de trayectoria más larga y varios refinamientos para reducir el error sistemático, la que se aceptaría como la que proporcionó una medición definitiva del corrimiento al rojo. [p 4]
Después de evaluar varios emisores γ para su estudio, Pound y Rebka eligieron utilizar 57 Fe porque no requiere enfriamiento criogénico para exhibir emisión sin retroceso, tiene un coeficiente de conversión interna relativamente bajo [nota 2] de modo que está relativamente libre de emisiones de rayos X competitivas que habrían sido difíciles de distinguir de la transición de 14,4 keV, [nota 3] y su progenitor 57 Co tiene una vida media utilizable de 272 días. [5]
Pound y Rebka descubrieron que una gran fuente de error sistemático se debía a las variaciones de temperatura, que atribuyeron principalmente a un efecto Doppler relativista de segundo orden debido a las vibraciones reticulares. Una simple diferencia de temperatura de 1 °C entre el emisor y el absorbedor causaba un desplazamiento aproximadamente igual al efecto predicho de la dilatación del tiempo gravitacional. [p 7] [6]
También encontraron desfases de frecuencia entre las líneas de diferentes combinaciones de fuente y absorbedor, que se debían a la sensibilidad de la transición nuclear al entorno físico y químico de un átomo. [nota 4] Por lo tanto, necesitaban adoptar una metodología que les permitiera distinguir estos desfases de su medición del corrimiento al rojo gravitacional. También era necesario tener mucho cuidado en la preparación de las muestras, de lo contrario, las inhomogeneidades limitarían la nitidez de las líneas. [p 4]

El experimento se llevó a cabo en una torre del laboratorio Jefferson de la Universidad de Harvard que estaba, en su mayor parte, aislada vibracionalmente del resto del edificio. Un disco de hierro que contenía 57Co radiactivo difundido en su superficie se colocó en el centro de un transductor magnético ferroeléctrico o de bobina móvil (bobina de altavoz) que se colocó cerca del techo del edificio. Un absorbedor de 38 cm de diámetro que consistía en láminas cuadradas delgadas de hierro enriquecido a un nivel de 32% de 57Fe (en oposición a una abundancia natural del 2%), que se pegaron una al lado de la otra en un patrón plano sobre una hoja de Mylar, se colocó en el sótano. La distancia entre la fuente y el absorbedor era de 22,5 metros (74 pies). Los rayos gamma viajaron a través de una bolsa de Mylar llena de helio para minimizar la dispersión de los rayos gamma. Se colocó un contador de centelleo debajo del absorbedor para detectar los rayos gamma que pasaban a través. [5]
La bobina vibrante del altavoz impuso un desplazamiento Doppler que variaba continuamente sobre la fuente de rayos gamma. Sobre los movimientos sinusoidales del transductor se superponía el movimiento lento (normalmente de unos 0,01 mm/s) constante de un cilindro hidráulico esclavo impulsado por un cilindro maestro de diámetro pequeño controlado por un motor sincrónico. El movimiento del cilindro hidráulico se invertía varias veces durante cada ejecución de datos después de un número entero constante de vibraciones del transductor. Cada varios días, se invertía la posición de la fuente y el absorbedor de modo que la mitad de las ejecuciones de datos fueran de desplazamiento al azul y la otra mitad de desplazamiento al rojo. [5]
Se conectaron tres termopares montados en la fuente en forma de espiral y tres en el absorbedor a puentes de Wheatstone para medir las diferencias de temperatura entre la fuente y el absorbedor. Las diferencias de temperatura registradas se utilizaron para corregir los datos antes del análisis. [5]
Entre otros pasos utilizados para compensar posibles errores sistemáticos , Pound y Rebka variaron la frecuencia del altavoz entre 10 Hz y 50 Hz y probaron diferentes transductores (transductores ferroeléctricos versus bobinas de altavoz magnéticas de bobina móvil). [7]
Un monitor Mössbauer cerca de la fuente (no ilustrado) verificó posibles distorsiones de la señal de la fuente resultantes de que el conjunto cilindro/transductor se invirtiera regularmente de mirar hacia abajo a mirar hacia arriba. [5]

Aunque la línea de emisión sin retroceso de 14,4 keV del 57 Fe tenía un ancho medio de 1,13×10 −12 , el desplazamiento de frecuencia gravitacional previsto era de tan solo 2,5×10 −15 . La medición de esta diminuta cantidad de desplazamiento de frecuencia, 500 veces menor que el ancho medio, requirió un protocolo sofisticado para la adquisición y el análisis de datos. La mejor manera de medir un desplazamiento pequeño es a menudo mediante la "detección de pendiente", midiendo la resonancia no en su pico, sino comparando la curva de absorción cerca de sus puntos de pendiente máxima (puntos de inflexión) a cada lado del pico. [5]
La bobina del altavoz funcionaba normalmente a unos 74 Hz con una amplitud de velocidad máxima correspondiente al cambio máximo de absorción con la velocidad de la curva de resonancia para una combinación dada de fuente y absorbedor (normalmente alrededor de 0,10 mm/s). [nota 5] Los conteos que se recibían en los cuartos de ciclo del período de oscilación centrados alrededor de los máximos de velocidad se acumulaban en dos registros separados. Del mismo modo, los conteos recibidos con el cilindro hidráulico en movimiento inverso se acumulaban en otros dos registros separados, para un total de cuatro registros de conteos acumulados. [5]

Los movimientos combinados del transductor vibratorio y el cilindro hidráulico permitieron que los fotones entrantes se recolectaran en cuatro canales que representaban movimientos de fuente de +0,11 mm/s, +0,09 mm/s, -0,11 mm/s y -0,09 mm/s. En conjunto, funcionaban con un ciclo de trabajo del 50 %, de modo que, de, digamos, 80 millones de fotones entrantes, 10 millones encajarían en los intervalos de tiempo de cada uno de los cuatro canales de registro. A partir de estos recuentos, se pudo calcular la velocidad correspondiente a la máxima absorbancia. [5]
La precisión de la determinación del centro de la línea dependía de (1) la nitidez de la línea, (2) la profundidad del máximo de absorbancia y (3) el número total de conteos. Por lo general, lograron una profundidad máxima de absorbancia fraccional de aproximadamente 0,3 [5] y registraron alrededor de 1×10 10 rayos γ, de los cuales la mayoría no habrán tenido retroceso. [8] [nota 6]
Cada ejecución de datos arrojó once números, es decir, cuatro recuentos de registros de absorción, cuatro recuentos de registros de monitorización y tres diferencias de temperatura promedio. Los recuentos de registros se registraron generalmente después de doce ciclos completos de ida y vuelta del pistón hidráulico, donde cada inversión del movimiento del pistón ocurrió después de 22.000 períodos de vibración de la fuente. [5]
Las unidades de fuente y de absorción se intercambiaron cada varios días para permitir la comparación entre los resultados con los rayos gamma ascendentes y los rayos gamma descendentes. La combinación de datos de ejecuciones con un desplazamiento de frecuencia gravitacional de signo igual pero opuesto permitió eliminar el desplazamiento de frecuencia fijo entre una combinación dada de fuente/objetivo mediante sustracción. [5]
En su artículo de 1960, Pound y Rebka presentaron datos de los primeros cuatro días de conteo. Seis ejecuciones con la fuente en la parte inferior, después de la corrección de temperatura, dieron un cambio de frecuencia fraccionaria promedio ponderado entre la fuente y el absorbedor de −(19,7±0,8)×10 −15 . Ocho ejecuciones con la fuente en la parte superior, después de la corrección de temperatura, dieron un cambio de frecuencia fraccionaria promedio ponderado de −(15,5±0,8)×10 −15 . [p 4]
Los cambios de frecuencia, tanto hacia arriba como hacia abajo, fueron negativos porque la magnitud de la diferencia de frecuencia inherente de la combinación fuente/absorbente excedió considerablemente la magnitud de los corrimientos al rojo/azul gravitacionales esperados. Al tomar la mitad de la suma de los promedios ponderados se obtuvo la diferencia de frecuencia inherente de la combinación fuente/absorbente, −(17,6±0,6)×10 −15 . Al tomar la mitad de la diferencia de los promedios ponderados se obtuvo el cambio de frecuencia fraccionario neto debido a la dilatación del tiempo gravitacional, −(2,1±0,5)×10 −15 . [p 4]
Durante los diez días completos de recopilación de datos, calcularon un cambio de frecuencia fraccionaria neta debido a la dilatación del tiempo gravitacional de −(2,56±0,25)×10 −15 , que corresponde al valor previsto con un margen de error del 10%. [p 4]
En los años siguientes, el laboratorio de Pound publicó sucesivos refinamientos de la medición del corrimiento al rojo gravitacional, alcanzando finalmente el nivel del 1% en 1964. [p 9] [1]
En los años posteriores a la serie de mediciones realizadas por el laboratorio de Pound, varias pruebas que utilizaban otras tecnologías establecieron la validez del corrimiento al rojo gravitacional/dilatación del tiempo con una precisión cada vez mayor. Un ejemplo notable fue el experimento Gravity Probe A de 1976, que utilizó un máser de hidrógeno espacial para aumentar la precisión de la medición a aproximadamente el 0,01 %. [p 10]
Desde un punto de vista de ingeniería, después del lanzamiento del Sistema de Posicionamiento Global (que depende de la relatividad general para su correcto funcionamiento [9] ) y su integración en la vida cotidiana, el corrimiento al rojo gravitacional/dilatación del tiempo ya no se considera un fenómeno teórico que requiere pruebas, sino que se considera una preocupación práctica de ingeniería en varios campos que requieren una medición precisa, junto con la relatividad especial . [10]
Sin embargo, desde un punto de vista teórico, la situación del corrimiento al rojo gravitacional/dilatación del tiempo es bastante diferente. Es un hecho ampliamente reconocido que la relatividad general, a pesar de tener en cuenta todos los datos recopilados hasta la fecha, no puede representar una teoría definitiva de la naturaleza. [11]
El principio de equivalencia (PE) se encuentra en el corazón de la teoría general de la relatividad. La mayoría de las alternativas propuestas a la relatividad general predicen la violación del PE en algún nivel. El PE incluye tres hipótesis: [11]
Las mediciones del corrimiento al rojo gravitacional proporcionan una medida directa del LPI. De las tres hipótesis que sustentan el principio de equivalencia, el LPI ha sido, con diferencia, la que se ha determinado con menos precisión. Por tanto, ha habido un incentivo considerable para mejorar las mediciones del corrimiento al rojo gravitacional tanto en el laboratorio como mediante observaciones astronómicas. [11] Por ejemplo, se espera que la muy esperada y muy retrasada misión del Conjunto de Relojes Atómicos en el Espacio (ACES) de la Agencia Espacial Europea mejore las mediciones anteriores en un factor de 35. [p 11]