

La calculadora de Pascal (también conocida como máquina aritmética o Pascalina ) es una calculadora mecánica inventada por Blaise Pascal en 1642. Pascal se vio impulsado a desarrollar una calculadora por los laboriosos cálculos aritméticos requeridos por el trabajo de su padre como supervisor de impuestos en Rouen . [2] Diseñó la máquina para sumar y restar dos números directamente y para realizar multiplicaciones y divisiones mediante sumas o restas repetidas.
La calculadora de Pascal fue especialmente exitosa en el diseño de su mecanismo de acarreo, que suma 1 a 9 en un dial, y acarrea 1 al siguiente dial cuando el primer dial cambia de 9 a 0. Su innovación hizo que cada dígito fuera independiente del estado de los demás, lo que permitió que múltiples acarreos pasaran rápidamente de un dígito a otro independientemente de la capacidad de la máquina. Pascal también fue el primero en reducir y adaptar para su propósito un engranaje de linterna , utilizado en relojes de torreta y ruedas hidráulicas . Esta innovación permitió que el dispositivo resistiera la fuerza de cualquier entrada del operador con muy poca fricción añadida.
Pascal diseñó la máquina en 1642. [3] Después de 50 prototipos , presentó el dispositivo al público en 1645, dedicándolo a Pierre Séguier , entonces canciller de Francia . [4] Pascal construyó alrededor de veinte máquinas más durante la siguiente década, muchas de las cuales mejoraron su diseño original. En 1649, el rey Luis XIV de Francia le dio a Pascal un privilegio real (similar a una patente ), que le proporcionó el derecho exclusivo a diseñar y fabricar máquinas calculadoras en Francia. Actualmente existen nueve calculadoras Pascal; [5] la mayoría están en exhibición en museos europeos.
Muchas calculadoras posteriores se inspiraron directamente o fueron moldeadas por las mismas influencias históricas que llevaron a la invención de Pascal. Gottfried Leibniz inventó sus ruedas de Leibniz después de 1671, después de intentar agregar una función de multiplicación automática a la Pascalina. [6] En 1820, Thomas de Colmar diseñó su aritmómetro , la primera calculadora mecánica lo suficientemente fuerte y confiable como para ser utilizada a diario en un entorno de oficina. No está claro si alguna vez vio el dispositivo de Leibniz, pero lo reinventó o utilizó la invención de Leibniz del tambor de pasos.

Blaise Pascal empezó a trabajar en su calculadora en 1642, cuando tenía 18 años. Había estado ayudando a su padre, que trabajaba como comisario de Hacienda, y buscaba producir un dispositivo que pudiera reducir parte de su carga de trabajo. Pascal recibió un privilegio real en 1649 que le otorgaba derechos exclusivos para fabricar y vender máquinas calculadoras en Francia.
En 1654 había vendido unas veinte máquinas (de las cuales sólo se sabe que hoy existen nueve [7] ), pero el coste y la complejidad de la Pascalina supusieron una barrera para seguir vendiéndolas y la producción cesó ese año. Para entonces, Pascal ya se había dedicado al estudio de la religión y la filosofía , lo que nos dio las Lettres provinciales y las Pensées .
La celebración del tricentenario de la invención de la calculadora mecánica por parte de Pascal tuvo lugar durante la Segunda Guerra Mundial , cuando Francia estaba ocupada por Alemania, por lo que la celebración principal se llevó a cabo en Londres, Inglaterra. Los discursos pronunciados durante el evento destacaron los logros prácticos de Pascal cuando ya era conocido en el campo de las matemáticas puras, y su imaginación creativa, junto con lo adelantados que estaban a su tiempo tanto la máquina como su inventor. [8]


La calculadora tenía diales de metal con radios, con los dígitos del 0 al 9 desplegados alrededor de la circunferencia de cada rueda. Para ingresar un dígito, el usuario colocaba un lápiz en el espacio correspondiente entre los radios y giraba el dial hasta que se alcanzaba un tope de metal en la parte inferior, de manera similar a como se usa el dial giratorio de un teléfono. Esto mostraba el número en las ventanas de la parte superior de la calculadora. Luego, uno simplemente volvía a marcar el segundo número que se iba a sumar, lo que hacía que la suma de ambos números apareciera en el acumulador.
Cada cuadrante está asociado a una ventana de visualización de un dígito situada directamente encima de él, que muestra el valor del acumulador para esta posición. El complemento de este dígito, en la base de la rueda (6, 10, 12, 20), se muestra justo encima de este dígito. Una barra horizontal oculta todos los números del complemento cuando se desliza hacia la parte superior, o todos los números directos cuando se desliza hacia el centro de la máquina. De este modo, muestra el contenido del acumulador o el complemento de su valor.
Como los engranajes de la calculadora giraban en una sola dirección, no era posible sumar directamente los números negativos. Para restar un número de otro, se utilizaba el método del complemento a nueve. Las únicas dos diferencias entre una suma y una resta son la posición de la barra de visualización (directa frente a complementaria) y la forma en que se introduce el primer número (directa frente a complementaria).
En el caso de una rueda de 10 dígitos (N), la rueda exterior fija está numerada del 0 al 9 (N-1). Los números se escriben de manera decreciente en el sentido de las agujas del reloj desde la parte inferior izquierda hasta la parte inferior derecha de la palanca de tope. Para sumar un 5, hay que introducir un estilete entre los radios que rodean el número 5 y girar la rueda en el sentido de las agujas del reloj hasta la palanca de tope. El número que aparece en el registro de visualización correspondiente se incrementará en 5 y, si se produce una transferencia de acarreo, el registro de visualización situado a la izquierda de este se incrementará en 1. Para sumar 50, se utiliza la rueda de entrada de decenas (segundo dial desde la derecha en una máquina decimal), para sumar 500, se utiliza la rueda de entrada de centenas, etc.
En todas las ruedas de todas las máquinas conocidas, excepto en la máquina Tardive , [9] se marcan dos radios adyacentes; estas marcas difieren de una máquina a otra. En la rueda de la imagen de la derecha, son puntos perforados, en la máquina de topografía están tallados; algunas son simplemente arañazos o marcas hechas con un poco de barniz, [10] algunas incluso estaban marcadas con pequeños trozos de papel. [11]
Estas marcas se utilizan para poner el cilindro correspondiente en su número máximo, listo para ser puesto a cero nuevamente. Para ello, el operador inserta el estilete entre estos dos radios y gira la rueda hasta el tope de la palanca. Esto funciona porque cada rueda está directamente vinculada a su cilindro de visualización correspondiente (gira automáticamente un número durante una operación de transporte). Para marcar los radios durante la fabricación, se puede mover el cilindro de manera que se muestre su número más alto y luego marcar el radio debajo de la palanca de parada y el que está a la derecha de este.
Cuatro de las máquinas conocidas tienen ruedas internas de complementos, que se usaban para ingresar el primer operando en una resta. Están montadas en el centro de cada rueda de metal con radios y giran con ella. La rueda que se muestra en la imagen de arriba tiene una rueda interna de complementos, pero los números escritos en ella son apenas visibles. En una máquina decimal, los dígitos del 0 al 9 están grabados en el sentido de las agujas del reloj, con cada dígito colocado entre dos radios de modo que el operador puede inscribir directamente su valor en la ventana de complementos colocando su estilete entre ellos y girando la rueda en el sentido de las agujas del reloj hasta el tope. [12] Las marcas en dos radios adyacentes flanquean el dígito 0 inscrito en esta rueda.
En cuatro de las máquinas conocidas, encima de cada rueda hay una pequeña rueda de cociente montada en la barra de visualización. Estas ruedas de cociente, que son ajustadas por el operador, tienen números del 1 al 10 inscritos en el sentido de las agujas del reloj en sus periferias (incluso encima de una rueda no decimal). Las ruedas de cociente parecen haber sido utilizadas durante una división para memorizar el número de veces que se restaba el divisor en cada índice dado. [13]


Pascal probó 50 prototipos antes de decidirse por su diseño final; sabemos que empezó con una especie de mecanismo de reloj calculador que aparentemente "funciona mediante resortes y que tiene un diseño muy simple", que se utilizó "muchas veces" y que se mantuvo "en condiciones de funcionamiento". Sin embargo, "mientras lo mejoraba constantemente", encontró motivos para intentar hacer que todo el sistema fuera más fiable y robusto. [14] Finalmente, adoptó un componente de los relojes muy grandes, reduciendo y adaptando para su propósito los robustos engranajes que se pueden encontrar en un mecanismo de reloj de torreta llamado engranaje de linterna , derivado a su vez de un mecanismo de rueda hidráulica. Este podría manejar fácilmente la fuerza de la entrada de un operador. [15]
Pascal adaptó un mecanismo de trinquete y trinquete a su propio diseño de rueda de torreta; el trinquete evita que la rueda gire en sentido contrario a las agujas del reloj durante la entrada de datos del operador, pero también se utiliza para posicionar con precisión la rueda de visualización y el mecanismo de transporte para el siguiente dígito cuando se empuja hacia arriba y aterriza en su siguiente posición. Debido a este mecanismo, cada número que se muestra está perfectamente centrado en la ventana de visualización y cada dígito está posicionado con precisión para la siguiente operación. Este mecanismo se movería seis veces si el operador marcara un seis en su rueda de entrada asociada.

El sautoir es la pieza central del mecanismo de transporte de la pascalina. En su "Avis nécessaire...", Pascal señaló que una máquina con 10.000 ruedas funcionaría tan bien como una máquina con dos ruedas porque cada rueda es independiente de la otra. Cuando llega el momento de propagar un transporte, el sautoir, bajo la única influencia de la gravedad, [16] es lanzado hacia la siguiente rueda sin ningún contacto entre las ruedas. Durante su caída libre, el sautoir se comporta como un acróbata que salta de un trapecio al siguiente sin que los trapecios se toquen entre sí ("sautoir" proviene del verbo francés sauter , que significa saltar). Todas las ruedas (incluidos los engranajes y el sautoir) tienen, por lo tanto, el mismo tamaño y peso independientemente de la capacidad de la máquina.
Pascal utilizó la gravedad para armar los sautoirs. Para armar completamente un sautoir, hay que girar la rueda cinco pasos, del 4 al 9, pero la transferencia de carga moverá la siguiente rueda solo un paso. Por lo tanto, se acumula mucha energía extra durante el armado de un sautoir.
Todos los sautoirs se arman mediante una entrada del operador o un carry forward. Para poner a cero una máquina de 10.000 ruedas, si existiera, el operador tendría que poner cada rueda a su máximo y luego añadir un 1 a la rueda de "unidad". El carry haría girar cada rueda de entrada una por una en un efecto dominó muy rápido y todos los registros de visualización se restablecerían.
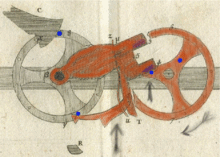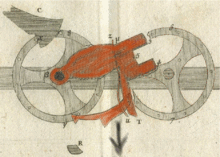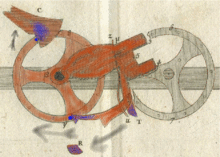
La transmisión de carga tiene tres fases:
La Pascaline es una máquina sumadora directa (no tiene manivela), por lo que el valor de un número se suma al acumulador a medida que se va ingresando. Al mover una barra de visualización, el operador puede ver el número almacenado en la calculadora o el complemento de su valor. Las restas se realizan como sumas utilizando algunas propiedades de la aritmética del complemento a 9.
El complemento a 9 de cualquier número decimal de un dígito d es 9- d . Por lo tanto, el complemento a 9 de 4 es 5 y el complemento a 9 de 9 es 0. De manera similar, el complemento a 11 de 3 es 8.
En una máquina decimal con n diales el complemento a 9 de un número A es:
y por lo tanto el complemento a 9 de (AB) es:
En otras palabras, el complemento a 9 de la diferencia de dos números es igual a la suma del complemento a 9 del minuendo sumado al sustraendo. El mismo principio es válido y puede emplearse con números compuestos por dígitos de bases diversas (base 6, 12, 20), como en las máquinas de agrimensura o de contabilidad.
Esto también puede extenderse a:
Este principio se aplicó a la Pascalina:
La máquina debe ponerse a cero antes de cada nueva operación. Para restablecer la máquina, el operador debe poner todas las ruedas al máximo, utilizando las marcas de dos radios adyacentes, y luego sumar 1 a la rueda más a la derecha. [17]
El método de puesta a cero que eligió Pascal, que propaga un acarreo a través de la máquina, es la tarea más exigente para una calculadora mecánica y demuestra, antes de cada operación, que la máquina está completamente funcional. Esto es un testimonio de la calidad de la Pascalina porque ninguna de las críticas del siglo XVIII a la máquina mencionaba un problema con el mecanismo de acarreo y, sin embargo, esta característica fue puesta a prueba en todas las máquinas, mediante sus reinicios, todo el tiempo. [18]
Las adiciones se realizan con la barra de visualización movida más cerca del borde de la máquina, mostrando el valor directo del acumulador.
Después de poner a cero la máquina, los números se marcan uno tras otro.
La siguiente tabla muestra todos los pasos necesarios para calcular 12,345 + 56,789 = 69,134
Las restas se realizan con la barra de visualización movida más cercana al centro de la máquina mostrando el valor del complemento del acumulador.
El acumulador contiene durante el primer paso y después de sumar B. Al mostrar esos datos en la ventana de complemento, el operador ve que es A y luego que es . Parece una suma, ya que las únicas dos diferencias entre una suma y una resta son la posición de la barra de visualización (directa versus complementaria) y la forma en que se ingresa el primer número (directa versus complementaria).
La siguiente tabla muestra todos los pasos necesarios para calcular 54.321-12.345=41.976
Las pascalinas se comercializaban en versiones decimales y no decimales, ambas de las cuales se pueden ver en los museos actuales. Fueron diseñadas para su uso por científicos, contables y topógrafos. La pascalina más sencilla tenía cinco diales; las variantes posteriores tenían hasta diez diales.
El sistema monetario francés contemporáneo utilizaba libras , soles y deniers , con 20 soles por libra y 12 deniers por sol . La longitud se medía en toesas , pies , pulgadas y líneas, con 6 pies por toesa , 12 pulgadas por pie y 12 líneas por pulgada . Por lo tanto, la pascalina necesitaba ruedas en base 6, 10, 12 y 20. Las ruedas no decimales siempre se ubicaban antes de la parte decimal.
En una máquina de contabilidad (..10,10,20,12), la parte decimal contaba el número de libras (20 soles ), soles (12 deniers ) y deniers . En una máquina de agrimensor (..10,10,6,12,12), la parte decimal contaba el número de toesas (6 pies ), pies (12 pouces ), pouces (12 lines ) y lines . Las máquinas científicas solo tenían ruedas decimales.
Se resalta la parte decimal de cada máquina.
El sistema métrico fue adoptado en Francia el 10 de diciembre de 1799, momento en el que el diseño básico de Pascal había inspirado a otros artesanos, aunque con una similar falta de éxito comercial.
La mayoría de las máquinas que han sobrevivido a los siglos son de tipo contable. Siete de ellas se encuentran en museos europeos, una pertenece a la corporación IBM y otra está en manos privadas.

Pascal planeó distribuir la Pascalina ampliamente para reducir la carga de trabajo de las personas que necesitaban realizar cálculos aritméticos laboriosos. [24] Inspirándose en su padre, un comisionado de impuestos , Pascal esperaba proporcionar un atajo a las horas de procesamiento de números que realizaban los trabajadores en profesiones como las matemáticas, la física, la astronomía, etc. [25] Pero, debido a las complejidades del dispositivo, la relación que Pascal tenía con los artesanos y las leyes de propiedad intelectual en las que influyó, la producción de la Pascalina fue mucho más limitada de lo que había imaginado. Solo se produjeron 20 Pascalinas durante los 10 años posteriores a su creación. [26]
En 1649, el rey Luis XIV de Francia le dio a Pascal un privilegio real (un precursor de la patente ), que le otorgaba el derecho exclusivo de diseñar y fabricar máquinas calculadoras en Francia, lo que permitió que la Pascaline fuera la primera calculadora vendida por un distribuidor. [27] Pascal temía que los artesanos no pudieran reproducir con precisión su Pascaline, lo que daría lugar a copias falsas que arruinarían su reputación junto con la reputación de su máquina. [24] En 1645, para controlar la producción de su invento, Pascal escribió a Monseigneur Le Chancelier (el canciller de Francia, Pierre Séguier ) en su carta titulada "La Machine d'arithmétique. Lettre dédicatoire à Monseigneur le Chancelier". [24] Pascal solicitó que no se fabricara ninguna Pascaline sin su permiso. [24] Su ingenio se ganó el respeto del rey Luis XIV de Francia, quien le concedió su solicitud, pero tuvo un precio; Los artesanos no podían experimentar legalmente con el diseño de Pascal ni tampoco podían distribuir su máquina sin su permiso o guía.
Pascal vivió en Francia durante el Antiguo Régimen . Durante su tiempo, los artesanos en Europa se organizaron cada vez más en gremios , como los relojeros ingleses que formaron el gremio de relojeros en 1631, a mitad de camino de los esfuerzos de Pascal por crear la calculadora. Esto afectó la capacidad de Pascal para reclutar talentos, ya que los gremios a menudo reducían el intercambio de ideas y el comercio; a veces, los artesanos retenían su trabajo por completo para rebelarse contra los nobles. Por lo tanto, Pascal estaba en un mercado que tenía escasez de habilidades y trabajadores dispuestos. [28] Es importante destacar que los artesanos no eran tan libres como los intelectuales para crear la máquina: Gottfried Leibniz , quien construyó sobre la calculadora de Pascal más tarde en el siglo XVII, vio detenido el progreso de su máquina debido a que su artesano vendió las partes de la máquina para obtener solvencia financiera. [29]
La propia conducta de Pascal provocó dificultades a la hora de reclutar artesanos para su proyecto, debido a su creencia de que las cuestiones de la mente prevalecían sobre las del cuerpo. Pascal no estaba solo, ya que muchos filósofos naturales de su tiempo tenían una comprensión hilomórfica del proceso de invención: las ideas preceden a la materialización, como la forma precede a la materia. Esto naturalmente llevó a un énfasis en la pureza teórica y a una subestimación del trabajo práctico. Como Pascal describió a los artesanos: “[ellos] trabajan a tientas, es decir, sin ciertas medidas y proporciones reguladas por el arte, sin producir nada que corresponda a lo que habían buscado, o, lo que es más, hacen aparecer un pequeño monstruo al que le faltan sus miembros principales, siendo los otros deformados, carentes de toda proporción”. [30]

Pascal llevó a cabo su proyecto con esta jerarquía en mente: él inventaba y pensaba, mientras que los artesanos simplemente ejecutaban. Ocultó la teoría a los artesanos, promoviendo en cambio que simplemente recordaran qué hacer, no necesariamente por qué debían hacerlo, es decir, hasta que “la práctica haya hecho que las reglas de la teoría sean tan comunes que [las reglas] finalmente se hayan reducido al arte”. Esto se originó en su falta de fe no solo en el proceso de trabajo artesanal, sino en los propios artesanos: “los artesanos no pueden regularse a sí mismos para producir máquinas unificadas de manera autónoma”. [30]
Por el contrario, Samuel Morland , uno de los contemporáneos de Pascal que también trabajó en la creación de una máquina calculadora, probablemente tuvo éxito debido a su capacidad para mantener buenas relaciones con sus artesanos. Morland atribuyó con orgullo parte de su invención a los artesanos por su nombre, algo extraño para un noble que hiciera por un plebeyo en ese momento. Morland pudo reclutar a los mejores talentos de Europa. Su primer artesano fue el famoso Peter Blondeau , que ya había recibido protección y reconocimiento del estadista francés Richelieu por sus contribuciones en la producción de monedas para Inglaterra. Los otros artesanos de Morland eran igualmente hábiles: el tercero, el holandés John Fromanteel , provenía de una famosa familia holandesa que fue pionera en el reloj de péndulo. [30]
Al final, Pascal logró consolidar su nombre como el único creador de la Pascalina. La patente real establece que fue invención exclusiva suya. [31]


Además de ser la primera máquina calculadora hecha pública en su época, la pascalina también es:
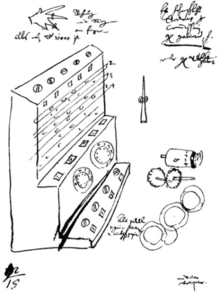
En 1957, Franz Hammer, biógrafo de Johannes Kepler , anunció el descubrimiento de dos cartas que Wilhelm Schickard había escrito a su amigo Johannes Kepler en 1623 y 1624 que contienen los dibujos de un reloj calculador en funcionamiento previamente desconocido, anterior al trabajo de Pascal por veinte años. [36] La carta de 1624 afirmaba que la primera máquina construida por un profesional había sido destruida en un incendio durante su construcción y que abandonaba su proyecto. [37] Después de un examen cuidadoso se descubrió, en contradicción con la comprensión de Franz Hammer, que los dibujos de Schickard se habían publicado al menos una vez por siglo a partir de 1718. [38]
Bruno von Freytag Loringhoff, profesor de matemáticas de la Universidad de Tubinga, construyó la primera réplica de la máquina de Schickard, pero no sin añadir ruedas y muelles para terminar el diseño. [39] Este detalle no se describe en las dos cartas y dibujos supervivientes de Schickard. Se encontró un problema en el funcionamiento de la máquina de Schickard, según las notas supervivientes, después de que se construyeran las réplicas. [40] La máquina de Schickard utilizaba ruedas de reloj que se hicieron más fuertes y, por tanto, más pesadas, para evitar que se dañaran con la fuerza de una entrada del operador. Cada dígito utilizaba una rueda de visualización, una rueda de entrada y una rueda intermedia. Durante una transferencia de acarreo, todas estas ruedas engranaban con las ruedas del dígito que recibía el acarreo. La fricción y la inercia acumuladas de todas estas ruedas podrían "... potencialmente dañar la máquina si fuera necesario propagar un acarreo a través de los dígitos, por ejemplo, como sumar 1 a un número como 9.999". [41] La gran innovación de la calculadora de Pascal fue que fue diseñada de manera que cada rueda de entrada es totalmente independiente de todas las demás y los acarreos se propagan en secuencia. Pascal eligió, para su máquina, un método de puesta a cero que propaga un acarreo a través de la máquina. [17] Es la operación más exigente de ejecutar para una calculadora mecánica y demostró, antes de cada operación, que el mecanismo de acarreo de la Pascalina era completamente funcional. Esto podría tomarse como un testimonio de la calidad de la Pascalina porque ninguna de las críticas del siglo XVIII a la máquina mencionó un problema con el mecanismo de acarreo y, sin embargo, esta característica fue completamente probada en todas las máquinas, mediante sus reinicios, todo el tiempo. [18]

Gottfried Leibniz comenzó a trabajar en su propia calculadora después de la muerte de Pascal. Primero intentó construir una máquina que pudiera multiplicar automáticamente mientras estaba sentado sobre la calculadora de Pascal, suponiendo incorrectamente que todos los diales de la calculadora de Pascal podían operarse al mismo tiempo. Aunque esto no pudo hacerse, fue la primera vez que se describió y utilizó un molinillo en el diseño de una calculadora.
Luego ideó un diseño competidor, el Reckoner por pasos , que pretendía realizar sumas, restas y multiplicaciones automáticamente y divisiones bajo el control del operador. Leibniz luchó durante cuarenta años para perfeccionar este diseño y produjo dos máquinas, una en 1694 y otra en 1706. [42] Solo se sabe que existe la máquina construida en 1694; fue redescubierta a fines del siglo XIX, después de haber pasado 250 años olvidada en un ático de la Universidad de Göttingen . [42]
Al inventor de la máquina calculadora alemana Arthur Burkhardt se le pidió que intentara poner la máquina de Leibniz en condiciones de funcionamiento. Su informe fue favorable excepto por la secuencia en el acarreo. [43] y "por lo tanto, especialmente en el caso de transferencias de acarreo múltiples, el operador tenía que verificar el resultado y corregir manualmente los posibles errores". [44] Leibniz no había logrado crear una calculadora que funcionara correctamente, pero había inventado la rueda de Leibniz , el principio de una calculadora mecánica de dos movimientos. También fue el primero en tener cursores para inscribir el primer operando y un carro móvil para los resultados.
Hubo cinco intentos adicionales de diseño de máquinas calculadoras de "entrada directa" en el siglo XVII (incluidos los diseños de Tito Burattini , Samuel Morland y René Grillet ).
Alrededor de 1660, Claude Perrault diseñó un ábaco rabdológico que a menudo se confunde con una calculadora mecánica porque tiene un mecanismo de acarreo entre los números. Pero en realidad es un ábaco, ya que requiere que el operador maneje la máquina de manera diferente cuando se realiza una transferencia de acarreo. [45]
La calculadora de Pascal fue la calculadora mecánica más exitosa desarrollada en el siglo XVII para la suma y resta de números grandes. El computador escalonado tenía un problema en el mecanismo de acarreo después de más de dos acarreos consecutivos, y los otros dispositivos tenían mecanismos de acarreo (una rueda dentada) que tenían una capacidad limitada para acarrear entre varios dígitos o no tenían mecanismo de acarreo entre los dígitos del acumulador.
Las máquinas calculadoras no se volvieron comercialmente viables hasta 1851, cuando Thomas de Colmar lanzó, después de treinta años de desarrollo, su aritmómetro simplificado , la primera máquina lo suficientemente potente como para ser utilizada a diario en un entorno de oficina. El aritmómetro fue diseñado en torno a las ruedas de Leibniz y utilizó inicialmente el método de complemento a 9 de Pascal para las restas.