
La paradoja de la rueda de Aristóteles es una paradoja o problema que aparece en la obra griega pseudoaristotélica Mechanica . Dice lo siguiente: Una rueda se representa en el espacio bidimensional como dos círculos . Su círculo exterior, más grande, es tangente a una superficie horizontal (por ejemplo, una carretera sobre la que rueda), mientras que el interior, más pequeño, tiene el mismo centro y está fijado rígidamente al más grande. (El círculo más pequeño podría ser el talón de un neumático, la llanta sobre la que está montado o el eje). Suponiendo que el círculo más grande rueda sin resbalar (o patinar) durante una revolución completa, las distancias recorridas por las circunferencias de ambos círculos son las mismas. La distancia recorrida por el círculo más grande es igual a su circunferencia , pero para el más pequeño es mayor que su circunferencia, creando así una paradoja.
La paradoja no se limita a las ruedas: otras cosas representadas en dos dimensiones muestran el mismo comportamiento, como un rollo de cinta o una botella o un frasco redondo típico enrollado sobre su lado (el círculo más pequeño sería la boca o el cuello del frasco o la botella).
En una versión alternativa del problema, el círculo más pequeño, en lugar del más grande, está en contacto con la superficie horizontal. Algunos ejemplos incluyen una rueda de tren típica, que tiene una brida, o una barra de pesas colocada a horcajadas sobre un banco. El educador y filósofo estadounidense Israel Drabkin llamó a estas versiones del Caso II de la paradoja [1] , y se aplica un análisis similar, pero no idéntico.
En la antigüedad, el problema de la rueda fue descrito en la obra griega Mechanica , tradicionalmente atribuida a Aristóteles, pero que se cree ampliamente que fue escrita por un miembro posterior de su escuela. [2] (Thomas Winter ha hecho la propuesta alternativa de que fue escrita por Arquitas . [3] ) También aparece en la Mechanica de Herón de Alejandría . [1] [4] En la versión aristotélica aparece como "Problema 24", donde la descripción de la rueda se da de la siguiente manera:
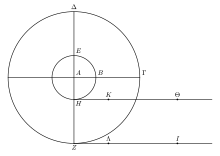
Sea, en efecto, un círculo mayor ΔZΓ , un círculo menor EHB y A en el centro de ambos; sea ZI la línea que el mayor desenrolla por sí mismo, y HK la que el menor desenrolla por sí mismo, igual a ZΛ . Cuando muevo el círculo menor, muevo el mismo centro, es decir, A ; sea el mayor unido a él. Cuando AB se hace perpendicular a HK , al mismo tiempo AΓ se hace perpendicular a ZΛ , de modo que siempre habrá recorrido una distancia igual, es decir, HK para la circunferencia HB , y ZΛ para ZΓ . Si el cuarto de círculo se desenrolla una distancia igual, es evidente que todo el círculo se desenrollará una distancia igual al círculo completo, de modo que cuando la línea BH llegue a K , la circunferencia ZΓ será ZΛ , y todo el círculo se desenrollará. De la misma manera, cuando muevo el círculo grande, ajustándolo al pequeño, siendo el centro de ambos el mismo, AB será perpendicular y perpendicular simultáneamente a AΓ , este último a ZI , el primero a HΘ . De modo que, cuando el uno haya completado una línea igual a HΘ , y el otro a ZI , y ZA se vuelva nuevamente perpendicular a ZΛ , y HA a HK , de modo que estarán como al principio en Θ e I . [5]
El problema se plantea entonces así:
Ahora bien, como el mayor no se detiene por el menor, de modo que permanezca durante cierto tiempo en el mismo punto, y como el menor no salta ningún punto, es extraño que el mayor recorra un camino igual al del menor, y que el menor recorra un camino igual al del mayor. Además, es notable que, aunque en cada caso sólo hay un movimiento, el centro que se mueve en un caso rueda una gran distancia y en el otro una distancia menor. [1]
El matemático Gerolamo Cardano analiza el problema de la rueda en su Opus novum de percentageibus numerorum de 1570 , [6] cuestionando la presunción de su análisis en términos de movimiento. [1] Mersenne lo analizó más a fondo en su Quaestiones Celeberrimae in Genesim de 1623 , [7] donde sugiere que el problema puede analizarse mediante un proceso de expansión y contracción de los dos círculos. Pero Mersenne no quedó satisfecho con su interpretación y escribió:
En verdad, nunca he podido descubrir, y no creo que nadie más haya podido descubrir, si el círculo más pequeño toca el mismo punto dos veces o avanza a saltos y deslizamientos. [1]
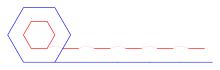
En su obra Dos nuevas ciencias , Galileo utiliza el problema de la rueda para argumentar a favor de un cierto tipo de atomismo . Comienza su análisis considerando un par de hexágonos concéntricos , en oposición a círculos. Al imaginar este hexágono "rodando" sobre una superficie, Galileo observa que el hexágono interior "salta" un poco de espacio con cada giro del exterior sobre una nueva cara. [8] Luego imagina qué sucedería con el límite a medida que el número de caras de un polígono se vuelve muy grande, y descubre que el pequeño espacio que "salta" el polígono interior se vuelve cada vez más pequeño. Escribe:
Por lo tanto, un polígono mayor que tiene mil lados pasa y mide una línea recta igual a su perímetro, mientras que al mismo tiempo el más pequeño pasa por una línea aproximadamente igual, pero compuesta interrumpidamente de mil pequeñas partículas iguales a sus mil lados con mil pequeños espacios vacíos interpuestos —pues podemos llamar a estos "vacíos" en relación con las mil rayitas tocadas por los lados del polígono. [8]
Como el círculo es simplemente el límite en el que el número de caras del polígono se vuelve infinito, Galileo descubre que la rueda de Aristóteles contiene material que está lleno de espacios infinitesimales o "vacíos", y que "los vacíos interpuestos no están cuantificados, sino que son infinitos". [8] Esto lo lleva a concluir que la creencia en los átomos -en el sentido de que la materia está "compuesta por infinitos átomos no cuantificables"- es suficiente para explicar el fenómeno. [8] Gilles de Roberval (1602-1675) también está asociado con este análisis.
Bernard Bolzano analizó la rueda de Aristóteles en Las paradojas del infinito (1851), un libro que influyó en Georg Cantor y en los pensadores posteriores sobre las matemáticas del infinito. Bolzano observa que existe una biyección entre los puntos de dos arcos cualesquiera similares, que se puede implementar trazando un radio, y señala que la historia de este hecho aparentemente paradójico se remonta a Aristóteles. [1]
El autor de Mathematical Fallacies and Paradoxes utiliza una moneda de diez centavos pegada a una de medio dólar (que representan círculos más pequeños y más grandes, respectivamente) con sus centros alineados y ambos fijados a un eje, como modelo para la paradoja. Escribe:
Ésta es, pues, la solución, o la clave. Aunque tengas cuidado de no dejar que la moneda de 50 centavos se deslice sobre la mesa, el «punto» que traza el segmento de línea al pie de la moneda de diez centavos gira y se desliza todo el tiempo. Se desliza con respecto a la mesa. Como la moneda de diez centavos no toca la mesa, no notas el deslizamiento. Si puedes hacer rodar la moneda de 50 centavos a lo largo de la mesa y al mismo tiempo hacer rodar la moneda de diez centavos (o mejor aún, el eje) a lo largo de un bloque de madera, puedes observar el deslizamiento. Si alguna vez has aparcado demasiado cerca de la acera, habrás notado el chirrido que hace el tapacubos al deslizarse (y rodar) sobre la acera mientras que tu neumático simplemente rueda sobre el pavimento. Cuanto más pequeño es el círculo pequeño en relación con el círculo grande, más se desliza el pequeño. Por supuesto, el centro de los dos círculos no gira en absoluto, por lo que se desliza durante todo el trayecto. [9]
La paradoja es que el círculo interior más pequeño se mueve 2π R , la circunferencia del círculo exterior más grande con radio R , en lugar de su propia circunferencia. Si el círculo interior se hiciera rodar por separado, se movería 2π r , su propia circunferencia con radio r . El círculo interior no está separado, sino conectado rígidamente al más grande.
Si el círculo más pequeño depende del más grande (caso I), el movimiento del círculo más grande obliga al más pequeño a recorrer la circunferencia del más grande. Si el círculo más grande depende del más pequeño (caso II), entonces el movimiento del círculo más pequeño obliga al círculo más grande a recorrer la circunferencia del círculo más pequeño. Esta es la solución más simple.

Esta solución considera la transición desde la posición inicial a la final. Sea Pb un punto en el círculo más grande y Ps un punto en el círculo más pequeño, ambos en el mismo radio. Por conveniencia, supongamos que ambos están directamente debajo del centro, de manera análoga a las dos manecillas de un reloj que apuntan hacia las seis. Tanto Pb como Ps viajan en una trayectoria cicloide mientras ruedan juntos una revolución. [10]
Si bien cada uno viaja 2π R horizontalmente desde el principio hasta el final, la trayectoria cicloide de Ps es más corta y más eficiente que la de Pb . Pb viaja más arriba y más abajo de la trayectoria del centro (la única recta) que Ps .
Si Pb y Ps estuvieran en cualquier otro lugar de sus respectivos círculos, las trayectorias curvas tendrían la misma longitud. En resumen, el círculo más pequeño se mueve horizontalmente 2π R porque cualquier punto en el círculo más pequeño recorre una trayectoria más corta y, por lo tanto, más directa que cualquier punto en el círculo más grande.