Onda plana electromagnética monocromática.

En la relatividad general , el espaciotiempo de onda plana electromagnética monocromática es el análogo de las ondas planas monocromáticas conocidas por la teoría de Maxwell. La definición precisa de la solución es bastante complicada pero muy instructiva. ^{[¿ según quién? ]}

Cualquier solución exacta de la ecuación de campo de Einstein que modele un campo electromagnético debe tener en cuenta todos los efectos gravitacionales de la energía y la masa del campo electromagnético . Además del campo electromagnético, si no hay materia ni campos no gravitacionales presentes, las ecuaciones de campo de Einstein y las ecuaciones de campo de Maxwell deben resolverse simultáneamente .

En la teoría de campo del electromagnetismo de Maxwell , uno de los tipos más importantes de campo electromagnético son los que representan la radiación electromagnética de microondas . De estos, los ejemplos más importantes son las ondas planas electromagnéticas , en las que la radiación tiene frentes de onda planos que se mueven en una dirección específica a la velocidad de la luz. De ellas, las más básicas son las ondas planas monocromáticas , en las que sólo está presente un componente de frecuencia . Este es precisamente el fenómeno que presenta este modelo de solución, pero en términos de relatividad general.

Definición de la solución.

El tensor métrico de la solución exacta única que modela una onda plana electromagnética polarizada linealmente con amplitud q y frecuencia ω se puede escribir, en términos de coordenadas de Rosen, en la forma

${\displaystyle ds^{2}=-2\,du\,dv+C^{2}\left({\frac {q^{2}}{\omega ^{2}}},2{\frac {q^{2}}{\omega ^{2}}},\omega u\right)\,\left(dx^{2}+dy^{2}\right),\qquad -\infty <v,x,y<\infty ,\quad -u_{0}<u<u_{0}.}$

donde es la primera raíz positiva de C ( a , 2 a , ξ ) = 0 donde . En este gráfico, ∂ _u , ∂ _v son vectores de coordenadas nulas mientras que ∂ _x , ∂ _y son vectores de coordenadas espaciales . ${\displaystyle \xi ={\frac {u_{0}}{\omega }}}$ ${\displaystyle a={\frac {q^{2}}{\omega ^{2}}}}$

Aquí, el coseno de Mathieu C ( a , b , ξ ) es una función par que resuelve la ecuación de Mathieu y también toma el valor C ( a , b , 0) = 1 . A pesar del nombre, esta función no es periódica y no se puede escribir en términos de funciones sinusoidales o incluso hipergeométricas. (Consulte Función de Mathieu para obtener más información sobre la función coseno de Mathieu).

En la expresión de la métrica, observe que ∂ _u , ∂ _v son campos vectoriales nulos . Por lo tanto, ∂ _u + ∂ _v es un campo vectorial temporal , mientras que ∂ _u − ∂ _v , ∂ _x , ∂ _y son campos vectoriales espaciales .

Para definir el potencial vectorial del campo electromagnético, se puede tomar el potencial electromagnético de cuatro vectores

${\displaystyle {\vec {A}}={\frac {{\sqrt {2}}a\int C\left({\frac {u^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)\,\sin(\omega u)\,du}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}}\;\partial _{x}}$

Ésta es la especificación completa de un modelo matemático formulado en relatividad general.

Isometrías locales

Nuestro espacio-tiempo está modelado por una variedad de Lorentz que tiene algunas simetrías notables. Es decir, nuestro espacio-tiempo admite un grupo de autoisometrías de Lie de seis dimensiones. Este grupo es generado por un álgebra de Lie de seis dimensiones de campos vectoriales Killing . Una base conveniente consta de un campo vectorial nulo,

${\displaystyle {\vec {\xi }}_{1}=\partial _{v}}$

tres campos vectoriales espaciales,

${\displaystyle {\vec {\xi }}_{2}=\partial _{x},\;{\vec {\xi }}_{3}=\partial _{y},\;{\vec {\xi }}_{4}=-y\,\partial _{x}+x\,\partial _{y}}$

y dos campos vectoriales adicionales,

${\displaystyle {\begin{aligned}{\vec {\xi }}_{5}&=x\,\partial _{v}+\int {\frac {du}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}}\,\partial _{x}\\{\vec {\xi }}_{6}&=y\,\partial _{v}+\int {\frac {du}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}}\,\partial _{y}\end{aligned}}}$

Aquí, genere el grupo euclidiano , que actúa dentro de cada frente de onda plano, lo que justifica el nombre de onda plana para esta solución. Demuestre también que todas las direcciones no transversales son equivalentes. Esto corresponde al hecho de que en el espacio-tiempo plano, dos ondas planas en colisión siempre chocan de frente cuando se representan en el marco de Lorentz apropiado . ${\displaystyle {\vec {\xi }}_{2},\,{\vec {\xi }}_{3},\,{\vec {\xi }}_{4}}$ ${\displaystyle {\vec {\xi }}_{5},\,{\vec {\xi }}_{6}}$

Para referencia futura, tenga en cuenta que este grupo de autoisometrías de seis dimensiones actúa de manera transitiva para que nuestro espacio-tiempo sea homogéneo . Sin embargo, no es isotrópico , ya que se distinguen las direcciones transversales de las no transversales.

Una familia de observadores inerciales.

El campo del marco

${\displaystyle {\vec {e}}_{0}={\frac {1}{\sqrt {2}}}\left(\partial _{u}+\partial _{v}\right)}$

${\displaystyle {\vec {e}}_{1}={\frac {1}{\sqrt {2}}}\left(-\partial _{u}+\partial _{v}\right)}$

${\displaystyle {\vec {e}}_{2}={\frac {1}{C\left({\frac {q^{2}}{\omega ^{2}}},\,{\frac {2q^{2}}{\omega ^{2}}},\,\omega u\right)}}\partial _{x}}$

${\displaystyle {\vec {e}}_{3}={\frac {1}{C\left({\frac {q^{2}}{\omega ^{2}}},\,{\frac {2q^{2}}{\omega ^{2}}},\,\omega u\right)}}\partial _{y}}$

Representa el marco de Lorentz local definido por una familia de observadores inerciales no giratorios . Eso es,

${\displaystyle \nabla _{{\vec {e}}_{0}}{\vec {e}}_{0}=0}$

lo que significa que las curvas integrales del campo vectorial unitario temporal e ₀ son geodésicas temporales , y también

${\displaystyle \nabla _{{\vec {e}}_{0}}{\vec {e}}_{1}=\nabla _{{\vec {e}}_{0}}{\vec {e}}_{2}=\nabla _{{\vec {e}}_{0}}{\vec {e}}_{3}=0}$

lo que significa que los campos vectoriales unitarios espaciales e ₁ , e ₂ , e ₃ no giran. (Son transportados por Fermi-Walker ). Aquí, hay un campo vectorial unitario de tipo temporal, mientras que son campos vectoriales unitarios de tipo espacial. ${\displaystyle {\vec {e}}_{0}}$ ${\displaystyle {\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3}}$

Los marcos inerciales no giratorios son lo más parecido que se puede llegar en el espacio-tiempo curvo a los marcos de Lorentz habituales conocidos de la relatividad especial , donde las transformaciones de Lorentz son simplemente cambios de un marco de Lorentz a otro.

El campo electromagnético

Con respecto a nuestro marco, el campo electromagnético obtenido del potencial dado anteriormente es

${\displaystyle {\vec {E}}=q\,\sin(\omega u)\,{\vec {e}}_{2}}$

${\displaystyle {\vec {B}}=-q\,\sin(\omega u)\,{\vec {e}}_{3}}$

Este campo electromagnético es una solución sin fuente de las ecuaciones de campo de Maxwell en el espacio-tiempo curvo particular definido por el tensor métrico anterior. Es una solución nula y representa una onda plana electromagnética sinusoidal transversal con amplitud q y frecuencia ω , que viaja en la dirección e ₁ . Cuando uno

• calcula el tensor tensión-energía T ^ab para el campo electromagnético dado,
• calcular el tensor de Einstein G ^ab para el tensor métrico dado,

se encuentra que se cumple la ecuación de campo de Einstein G ^ab = 8 πT ^ab . Esto es lo que se quiere decir al decir que existe una solución de electrovacío exacta .

En términos de nuestro marco, el tensor tensión-energía resulta ser

${\displaystyle T^{{\hat {j}}{\hat {k}}}={\frac {q^{2}\sin ^{2}(\omega u)}{4\pi }}{\begin{bmatrix}1&1&0&0\\1&1&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}}}$

Esta es la misma expresión que se encontraría en el electromagnetismo clásico (donde se desprecian los efectos gravitacionales de la energía del campo electromagnético) para el campo nulo dado anteriormente; la única diferencia es que ahora nuestro marco es una base anholonómica (ortonormal) en un espacio-tiempo curvo , en lugar de una base coordinada en un espacio-tiempo plano . (Ver campos de marco ).

Movimiento relativo de los observadores.

Se dice que la carta de Rosen se mueve comodamente con nuestra familia de observadores inerciales sin giro, porque las coordenadas ve − u , x , y son todas constantes a lo largo de cada línea mundial, dada por una curva integral del campo vectorial unitario temporal . Por tanto, en el gráfico de Rosen, estos observadores podrían parecer inmóviles. Pero, de hecho, están en relativo movimiento unos respecto de otros. Para ver esto, se debe calcular su tensor de expansión con respecto al marco dado anteriormente. Esto resulta ser ${\displaystyle {\vec {X}}={\vec {e}}_{0}}$

${\displaystyle \theta [{\vec {X}}]_{{\hat {i}}{\hat {j}}}={\frac {\omega }{\sqrt {2}}}\,{\frac {C^{\prime }({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u)}{C({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u)}}\,\operatorname {diag} (0,1,1)}$

dónde

${\displaystyle C^{\prime }(a,q,\xi )={\frac {\partial C(a,q,\xi )}{\partial \xi }}.}$

Los componentes que no desaparecen son idénticos y están

1. cóncavo hacia abajo ${\displaystyle -u_{0}<u<u_{0}}$
2. desaparece en tu = 0 .

Físicamente, esto significa que una pequeña "nube" esférica de nuestros observadores inerciales flota momentáneamente en u = 0 y luego comienza a colapsar, eventualmente atravesándose entre sí en u = u ₀ . Si se las imagina formando una nube tridimensional de partículas de prueba distribuidas uniformemente, este colapso se produce ortogonalmente a la dirección de propagación de la onda. La nube no muestra ningún movimiento relativo en la dirección de propagación, por lo que se trata de un movimiento puramente transversal .

Para (la aproximación de onda corta), se tiene aproximadamente ${\displaystyle {\frac {q}{\omega }}\ll 1}$

${\displaystyle g_{xx}\approx \cos(qu)^{2}}$

${\displaystyle \theta [{\vec {X}}]_{22}\approx -q\,\tan(qu)}$Por ejemplo, con , se tiene ${\displaystyle q=1/2,\omega =5}$

donde las expresiones exactas se representan en rojo y las aproximaciones de onda corta en verde.

El tensor de vorticidad de nuestra congruencia se desvanece de manera idéntica , por lo que las líneas mundiales de nuestros observadores son ortogonales a la hipersuperficie . El tensor de Riemann tridimensional de las hiperslices viene dado, con respecto a nuestro marco, por

${\displaystyle {{}^{3}R}_{1212}={{}^{3}R}_{1313}=q^{2}\,\sin(\omega u)^{2}}$

${\displaystyle {{}^{3}R}_{2323}={\frac {-\omega ^{2}}{2}}\,{\frac {C^{\prime }\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)^{2}}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)^{2}}}}$

La curvatura se divide claramente en onda (las curvaturas seccionales paralelas a la dirección de propagación) y fondo (la curvatura seccional transversal).

El tensor de curvatura de Riemann

Por el contrario, la descomposición de Bel del tensor de curvatura de Riemann, tomada con respecto a , es la simplicidad misma. El tensor electrogravítico , que representa directamente las aceleraciones de marea , es ${\displaystyle {\vec {X}}={\vec {e}}_{0}}$

${\displaystyle E[{\vec {X}}]_{{\hat {m}}{\hat {n}}}=q^{2}\,\sin(\omega u)^{2}\,\operatorname {diag} (0,1,1)}$

El tensor magnetogravítico , que representa directamente la fuerza de espín-espín en un giroscopio llevado por uno de nuestros observadores, es

${\displaystyle B[{\vec {X}}]_{{\hat {m}}{\hat {n}}}=q^{2}\,\sin(\omega u)^{2}{\begin{bmatrix}0&0&0\\0&0&-1\\0&1&0\end{bmatrix}}}$

(El tensor topogravítico , que representa las curvaturas seccionales espaciales , concuerda con el tensor electrogravítico).

Volviendo a observar nuestra gráfica del tensor métrico, se puede ver que el tensor de marea produce pequeñas aceleraciones relativas sinusoidales con período ω , que son puramente transversales a la dirección de propagación de la onda. El efecto gravitacional neto a lo largo de muchos períodos produce un ciclo de expansión y nuevo colapso de nuestra familia de observadores inerciales sin giro. Esto puede considerarse el efecto de la curvatura de fondo de la onda producida.

Este ciclo de expansión y colapso recuerda a los modelos cosmológicos FRW en expansión y colapso , y ocurre por una razón similar: la presencia de masa-energía no gravitacional. En los modelos FRW, esta energía masiva se debe a la masa de las partículas de polvo; aquí, se debe a la energía del campo de ondas electromagnéticas. Allí, el ciclo de expansión-recolapso comienza y termina con una fuerte singularidad de curvatura escalar ; aquí hay una mera singularidad coordinada (circunstancia que confundió mucho a Einstein y Rosen en 1937). Además, hay una pequeña modulación sinusoidal de la expansión y el retroceso.

Efectos ópticos

Un principio general sobre las ondas planas establece que no se puede ver el tren de ondas entrar en la estación, pero sí se puede verlo salir . Es decir, si uno mira a través de frentes de onda que se aproximan a objetos distantes, no verá distorsión óptica, pero si uno gira y mira a través de frentes de onda que se alejan a objetos distantes, verá distorsiones ópticas. Específicamente, la congruencia geodésica nula generada por el campo vectorial nulo tiene escalares ópticos que desaparecen , pero la congruencia geodésica nula generada por tiene escalares de torsión y corte que desaparecen, pero un escalar de expansión que no desaparece ${\displaystyle {\vec {k}}={\vec {e}}_{0}+{\vec {e}}_{1}}$ ${\displaystyle {\vec {\ell }}={\vec {e}}_{0}-{\vec {e}}_{1}}$

${\displaystyle \theta ={\sqrt {2}}\omega \,{\frac {C^{\prime }\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}}}$

Esto muestra que al mirar a través de frentes de onda salientes hacia objetos distantes, nuestros observadores inerciales que no giran verán cambiar su tamaño aparente de la misma manera que la expansión de la propia congruencia geodésica temporal.

El gráfico de Brinkmann

Una forma de ver rápidamente la plausibilidad de la afirmación de que u = u ₀ es una mera singularidad coordinada es recordar que nuestro espacio-tiempo es homogéneo , de modo que todos los eventos son equivalentes. Para confirmar esto directamente y estudiar desde una perspectiva diferente el movimiento relativo de nuestros observadores inerciales sin giro, se puede aplicar la transformación de coordenadas.

${\displaystyle u\to u}$

${\displaystyle v\to v-{\frac {\dot {r}}{2r}}\left(x^{2}+y^{2}\right)}$

${\displaystyle x\to x/r}$

${\displaystyle y\to y/r}$

dónde

${\displaystyle -{\frac {{\ddot {r}}(u)}{r(u)}}=q\sin(\omega u)^{2}}$

Esto lleva la solución a su representación en términos de coordenadas de Brinkmann :

${\displaystyle ds^{2}=-q\,\sin(\omega u)^{2}\,du^{2}-2\,du\,dv+dx^{2}+dy^{2},\qquad -\infty <u,v,x,y<\infty }$

Dado que se puede demostrar que las nuevas coordenadas están geodésicamente completas , las coordenadas de Brinkmann definen un gráfico de coordenadas global. En este gráfico, se puede ver que se produce una secuencia infinita de ciclos idénticos de expansión y colapso.

Cáusticos

En el gráfico de Brinkmann, nuestro campo de marco se vuelve bastante complicado:

${\displaystyle {\vec {e}}_{0}={\frac {\partial _{u}+\partial _{v}}{\sqrt {2}}}+\left\{{\frac {x^{2}+y^{2}}{\sqrt {2}}}\left(-q^{2}\sin(\omega u)^{2}+{\frac {\omega ^{2}}{2}}\,{\frac {C^{\prime }\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)^{2}}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)^{2}}}\right)\partial _{v}\right\}+\left\{{\frac {\omega }{2}}{\frac {C^{\prime }\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}}\left(x\partial _{x}+y\partial _{y}\right)\right\}}$

Etcétera. Naturalmente, si se calcula el tensor de expansión, el tensor electrogravítico, etc., se obtendrían las mismas respuestas que antes, pero expresadas en las nuevas coordenadas.

Llama la atención la simplicidad del tensor métrico en comparación con la complejidad del marco. El punto es que uno puede visualizar más fácilmente las cáusticas formadas por el movimiento relativo de nuestros observadores en el nuevo gráfico. Las curvas integrales del campo vectorial geodésico unitario temporal dan las líneas mundiales de nuestros observadores. En el gráfico de Rosen, aparecen como líneas de coordenadas verticales, ya que ese gráfico tiene movimiento común. ${\displaystyle {\vec {X}}={\vec {e}}_{0}}$

Para entender cómo aparece esta situación en la carta de Brinkmann, observe que cuando ω es extensivo, nuestro campo vectorial unitario geodésico temporal se vuelve aproximadamente

${\displaystyle {\vec {X}}\approx {\frac {\partial _{u}+\partial _{v}}{\sqrt {2}}}-q\tan(qu)\left(x\partial _{x}+y\partial _{y}\right)+{\frac {x^{2}+y^{2}}{\sqrt {2}}}\,\left(-q^{2}\sin(\omega u)^{2}+q^{2}\tan(qu)^{2}\right)\partial _{v}}$

Suprimiendo el último término, el resultado es

Movimiento aproximado de nuestra familia de observadores, representado en el gráfico de Brinkmann.

${\displaystyle {\vec {X}}\approx \partial _{t}-q\tan \left({\frac {qu}{\sqrt {2}}}\right)\left(x\partial _{x}+y\partial _{y}\right)}$

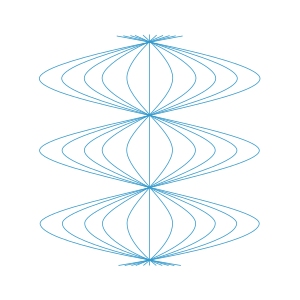
Se obtiene inmediatamente una curva integral que presenta ciclos de expansión y reconvergencia sinusoidales. Vea la figura, en la que el tiempo corre verticalmente y uno usa la simetría radial para suprimir una dimensión espacial. Esta figura muestra por qué hay una singularidad de coordenadas en la carta de Rosen; los observadores deben pasar unos junto a otros a intervalos regulares, lo cual es incompatible con la propiedad de comovimiento, por lo que la carta se descompone en estos lugares. Tenga en cuenta que esta figura sugiere incorrectamente que un observador es el "centro de atracción", por así decirlo, pero en realidad todos son completamente equivalentes , debido al gran grupo de simetría de este espacio-tiempo. Tenga en cuenta también que el movimiento relativo ampliamente sinusoidal de nuestros observadores es totalmente consistente con el comportamiento del tensor de expansión (con respecto al campo del marco correspondiente a nuestra familia de observadores) que se señaló anteriormente.

Vale la pena señalar que estos puntos un tanto complicados confundieron nada menos que a Albert Einstein en su artículo de 1937 sobre ondas gravitacionales (escrito mucho antes de que la maquinaria matemática moderna utilizada aquí fuera ampliamente apreciada en física).

Así, en el gráfico de Brinkmann, las líneas mundiales de nuestros observadores, en el caso de onda corta, son curvas periódicas que tienen forma sinusoidal con período , moduladas por perturbaciones sinusoidales mucho más pequeñas en la dirección nula ∂ _v y que tienen un período mucho más corto. . Los observadores periódicamente se expanden y contraen transversalmente a la dirección de propagación; este movimiento está modulado por un corto período de pequeñas perturbaciones de amplitud. ${\displaystyle 2\pi /q}$ ${\displaystyle 2\pi /\omega }$

Resumen

Comparando nuestra solución exacta con la onda plana electromagnética monocromática habitual tratada en la relatividad especial (es decir, como una onda en el espacio-tiempo plano, ignorando los efectos gravitacionales de la energía del campo electromagnético), se ve que la nueva característica sorprendente en la relatividad general es los ciclos de expansión y colapso experimentados por nuestros observadores, que se pueden atribuir a la curvatura del fondo , no a mediciones realizadas en tiempos y distancias cortas (del orden de la longitud de onda de la radiación electromagnética de microondas).

Ver también

• Argumento de las cuentas adhesivas , para un relato del artículo de 1937 de Einstein y Rosen aludido anteriormente.

Referencias

• Misner, Charles; Thorne, Kip S. y Wheeler, John Archibald (1973). Gravitación . San Francisco: WH Freeman . ISBN 0-7167-0344-0. Ver sección 35.11