Las ondas Lamb se propagan en placas sólidas o esferas. [1] Son ondas elásticas cuyo movimiento de partículas se encuentra en el plano que contiene la dirección de propagación de la onda y la dirección perpendicular a la placa. En 1917, el matemático inglés Horace Lamb publicó su clásico análisis y descripción de las ondas acústicas de este tipo. Sus propiedades resultaron ser bastante complejas. Un medio infinito admite solo dos modos de onda que viajan a velocidades únicas; pero las placas admiten dos conjuntos infinitos de modos de onda Lamb, cuyas velocidades dependen de la relación entre la longitud de onda y el espesor de la placa.
Desde la década de 1990, la comprensión y la utilización de las ondas Lamb han avanzado enormemente gracias al rápido aumento de la disponibilidad de potencia informática. Las formulaciones teóricas de Lamb han encontrado una aplicación práctica sustancial, especialmente en el campo de los ensayos no destructivos.
El término ondas de Rayleigh-Lamb engloba las ondas de Rayleigh , un tipo de onda que se propaga a lo largo de una única superficie. Tanto las ondas de Rayleigh como las de Lamb están limitadas por las propiedades elásticas de la superficie o superficies que las guían.

En general, las ondas elásticas en materiales sólidos [2] se guían por los límites de los medios en los que se propagan. Un enfoque para la propagación de ondas guiadas, ampliamente utilizado en acústica física, consiste en buscar soluciones sinusoidales a la ecuación de onda para ondas elásticas lineales sujetas a condiciones de contorno que representan la geometría estructural. Este es un problema clásico de valores propios .
Las ondas en placas fueron de las primeras ondas guiadas que se analizaron de esta manera. El análisis fue desarrollado y publicado en 1917 [3] por Horace Lamb , un líder en la física matemática de su época.
Las ecuaciones de Lamb se derivaron estableciendo un formalismo para una placa sólida que tiene una extensión infinita en las direcciones x e y , y un espesor d en la dirección z . Se postularon soluciones sinusoidales para la ecuación de onda , con desplazamientos x y z de la forma
Esta forma representa ondas sinusoidales que se propagan en la dirección x con una longitud de onda de 2π/k y una frecuencia de ω/2π. El desplazamiento es una función de x , z y t únicamente; no hay desplazamiento en la dirección y ni variación de ninguna cantidad física en la dirección y .
La condición física límite para las superficies libres de la placa es que el componente de tensión en la dirección z en z = +/- d /2 sea cero. Aplicando estas dos condiciones a las soluciones formalizadas anteriormente para la ecuación de onda, se puede encontrar un par de ecuaciones características. Estas son:
para modos simétricos y
para modos asimétricos, donde
En estas ecuaciones existe una relación entre la frecuencia angular ω y el número de onda k. Se utilizan métodos numéricos para hallar la velocidad de fase c p = fλ = ω/k y la velocidad de grupo c g = dω / dk , como funciones de d / λ o fd . c l y c t son las velocidades de onda longitudinal y de onda transversal respectivamente.
La solución de estas ecuaciones también revela la forma precisa del movimiento de la partícula, que las ecuaciones (1) y (2) representan sólo en forma genérica. Se encuentra que la ecuación (3) da lugar a una familia de ondas cuyo movimiento es simétrico respecto del plano medio de la placa (el plano z = 0), mientras que la ecuación (4) da lugar a una familia de ondas cuyo movimiento es antisimétrico respecto del plano medio. La figura 1 ilustra un miembro de cada familia.
Las ecuaciones características de Lamb se establecieron para ondas que se propagan en una placa infinita, un sólido isótropo homogéneo limitado por dos planos paralelos más allá de los cuales no puede propagarse energía de onda. Al formular su problema, Lamb confinó los componentes del movimiento de las partículas a la dirección de la normal de la placa ( dirección z ) y la dirección de propagación de la onda ( dirección x ). Por definición, las ondas de Lamb no tienen movimiento de partículas en la dirección y . El movimiento en la dirección y en las placas se encuentra en los llamados modos de onda SH o de corte horizontal. Estos no tienen movimiento en las direcciones x o z y, por lo tanto, son complementarios a los modos de onda de Lamb. Estos dos son los únicos tipos de onda que pueden propagarse con frentes de onda rectos e infinitos en una placa como se definió anteriormente.
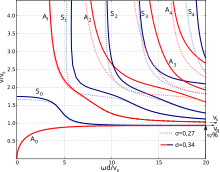
Las ondas Lamb presentan dispersión de velocidad, es decir, su velocidad de propagación c depende de la frecuencia (o longitud de onda), así como de las constantes elásticas y la densidad del material. Este fenómeno es fundamental para el estudio y la comprensión del comportamiento de las ondas en las placas. Físicamente, el parámetro clave es la relación entre el espesor de la placa d y la longitud de onda . Esta relación determina la rigidez efectiva de la placa y, por lo tanto, la velocidad de la onda. En aplicaciones tecnológicas, se utiliza un parámetro más práctico que se deriva fácilmente de esto, a saber, el producto del espesor por la frecuencia:
La relación entre velocidad y frecuencia (o longitud de onda) es inherente a las ecuaciones características. En el caso de la placa, estas ecuaciones no son simples y su solución requiere métodos numéricos. Este fue un problema insoluble hasta la llegada de la computadora digital cuarenta años después del trabajo original de Lamb. La publicación de "curvas de dispersión" generadas por computadora por Viktorov [4] en la ex Unión Soviética, Firestone seguida por Worlton en los Estados Unidos y eventualmente muchos otros llevaron la teoría de ondas de Lamb al ámbito de la aplicabilidad práctica. El software gratuito "Dispersion Calculator" (DC) [5] permite el cálculo de diagramas de dispersión para placas isotrópicas y muestras anisotrópicas multicapa. Las formas de onda experimentales observadas en las placas se pueden entender mediante interpretación con referencia a las curvas de dispersión.
Las curvas de dispersión (gráficos que muestran las relaciones entre la velocidad de onda, la longitud de onda y la frecuencia en sistemas dispersivos) se pueden presentar de varias formas. La forma que proporciona la mayor comprensión de la física subyacente tiene (frecuencia angular) en el eje y y k (número de onda) en el eje x . La forma utilizada por Viktorov, que permitió el uso práctico de las ondas Lamb, tiene la velocidad de onda en el eje y y , la relación espesor/longitud de onda, en el eje x . La forma más práctica de todas, cuyo mérito se debe a J. y H. Krautkrämer, así como a Floyd Firestone (quien, por cierto, acuñó la frase "ondas Lamb"), tiene la velocidad de onda en el eje y y fd , el producto frecuencia-espesor, en el eje x .
Las ecuaciones características de Lamb indican la existencia de dos familias completas de modos de onda sinusoidal en placas infinitas de ancho . Esto contrasta con la situación en medios ilimitados donde solo hay dos modos de onda, la onda longitudinal y la onda transversal o de corte . Al igual que en las ondas de Rayleigh que se propagan a lo largo de superficies libres individuales, el movimiento de partículas en las ondas de Lamb es elíptico con sus componentes x y z dependiendo de la profundidad dentro de la placa. [6] En una familia de modos, el movimiento es simétrico sobre el plano de espesor medio. En la otra familia es antisimétrico. El fenómeno de dispersión de velocidad conduce a una rica variedad de formas de onda observables experimentalmente cuando las ondas acústicas se propagan en placas. Es la velocidad de grupo c g , no la velocidad de fase mencionada anteriormente c o c p , la que determina las modulaciones observadas en la forma de onda observada. La apariencia de las formas de onda depende críticamente del rango de frecuencia seleccionado para la observación. Los modos flexural y extensional son relativamente fáciles de reconocer y esto se ha defendido como una técnica de prueba no destructiva .
Los modos de orden cero simétricos y antisimétricos merecen especial atención. Estos modos tienen "frecuencias nacientes" de cero. Por lo tanto, son los únicos modos que existen en todo el espectro de frecuencias desde cero hasta frecuencias infinitamente altas. En el rango de frecuencias bajas (es decir, cuando la longitud de onda es mayor que el espesor de la placa), estos modos a menudo se denominan "modo extensional" y "modo flexural", respectivamente, términos que describen la naturaleza del movimiento y las rigideces elásticas que gobiernan las velocidades de propagación. El movimiento elíptico de la partícula se produce principalmente en el plano de la placa para el modo extensional simétrico y perpendicular al plano de la placa para el modo flexural antisimétrico. Estas características cambian a frecuencias más altas.
Estos dos modos son los más importantes porque (a) existen en todas las frecuencias y (b) en la mayoría de las situaciones prácticas transportan más energía que los modos de orden superior.
El modo simétrico de orden cero (denominado S 0 ) se desplaza a la "velocidad de placa" en el régimen de baja frecuencia, donde se le denomina apropiadamente "modo extensional". En este régimen, la placa se estira en la dirección de propagación y se contrae correspondientemente en la dirección del espesor. A medida que aumenta la frecuencia y la longitud de onda se vuelve comparable con el espesor de la placa, la curvatura de la placa comienza a tener una influencia significativa en su rigidez efectiva. La velocidad de fase cae suavemente mientras que la velocidad de grupo cae algo precipitadamente hacia un mínimo. A frecuencias aún más altas, tanto la velocidad de fase como la velocidad de grupo convergen hacia la velocidad de onda de Rayleigh: la velocidad de fase desde arriba y la velocidad de grupo desde abajo.
En el límite de baja frecuencia para el modo extensional, los componentes z y x del desplazamiento de la superficie están en cuadratura y la relación de sus amplitudes está dada por: donde es el coeficiente de Poisson.
El modo antisimétrico de orden cero (designado A 0 ) es altamente dispersivo en el régimen de baja frecuencia, donde se lo denomina apropiadamente "modo de flexión" o "modo de flexión". Para frecuencias muy bajas (placas muy delgadas), las velocidades de fase y de grupo son proporcionales a la raíz cuadrada de la frecuencia; la velocidad de grupo es el doble de la velocidad de fase. Esta relación simple es una consecuencia de la relación rigidez/espesor para placas delgadas en flexión. A frecuencias más altas, donde la longitud de onda ya no es mucho mayor que el espesor de la placa, estas relaciones se rompen. La velocidad de fase aumenta cada vez menos rápidamente y converge hacia la velocidad de onda de Rayleigh en el límite de alta frecuencia. La velocidad de grupo pasa por un máximo, un poco más rápido que la velocidad de onda transversal, cuando la longitud de onda es aproximadamente igual al espesor de la placa. Luego converge, desde arriba, a la velocidad de onda de Rayleigh en el límite de alta frecuencia.
En experimentos que permiten excitar y detectar tanto el modo extensional como el flexural, el modo extensional suele aparecer como precursor de mayor velocidad y menor amplitud del modo flexural. El modo flexural es el que se excita con mayor facilidad de los dos y, a menudo, es el que transporta la mayor parte de la energía.
A medida que aumenta la frecuencia, aparecen los modos de onda de orden superior además de los modos de orden cero. Cada modo de orden superior “nace” en una frecuencia de resonancia de la placa y existe solo por encima de esa frecuencia. Por ejemplo, en una placa de acero de 3 ⁄ 4 pulgadas (19 mm) de espesor a una frecuencia de 200 kHz, están presentes los primeros cuatro modos de onda Lamb, y a 300 kHz, los primeros seis. Los primeros modos de orden superior se pueden observar claramente en condiciones experimentales favorables. En condiciones menos favorables, se superponen y no se pueden distinguir.
Los modos Lamb de orden superior se caracterizan por planos nodales dentro de la placa, paralelos a las superficies de la misma. Cada uno de estos modos existe sólo por encima de una determinada frecuencia que puede denominarse su "frecuencia naciente". No existe un límite de frecuencia superior para ninguno de los modos. Las frecuencias nacientes pueden representarse como las frecuencias resonantes de las ondas longitudinales o transversales que se propagan perpendicularmente al plano de la placa, es decir,
donde n es cualquier entero positivo. Aquí c puede ser la velocidad de onda longitudinal o la velocidad de onda transversal, y para cada conjunto resultante de resonancias los modos de onda Lamb correspondientes son alternativamente simétricos y antisimétricos. La interacción de estos dos conjuntos da como resultado un patrón de frecuencias nacientes que a primera vista parece irregular. Por ejemplo, en una placa de acero de 3/4 de pulgada (19 mm) de espesor que tiene velocidades longitudinales y transversales de 5890 m/s y 3260 m/s respectivamente, las frecuencias nacientes de los modos antisimétricos A 1 y A 2 son 86 kHz y 310 kHz respectivamente, mientras que las frecuencias nacientes de los modos simétricos S 1 , S 2 y S 3 son 155 kHz, 172 kHz y 343 kHz respectivamente.
En su frecuencia inicial, cada uno de estos modos tiene una velocidad de fase infinita y una velocidad de grupo de cero. En el límite de alta frecuencia, las velocidades de fase y de grupo de todos estos modos convergen a la velocidad de onda transversal. Debido a estas convergencias, las velocidades de Rayleigh y de onda transversal (que son muy cercanas entre sí) son de gran importancia en las placas gruesas. En términos simples, en términos del material de mayor importancia para la ingeniería, la mayor parte de la energía de onda de alta frecuencia que se propaga a grandes distancias en las placas de acero viaja a 3000–3300 m/s.
El movimiento de partículas en los modos de onda Lamb es en general elíptico, con componentes tanto perpendiculares como paralelos al plano de la placa. Estos componentes están en cuadratura, es decir, tienen una diferencia de fase de 90°. La magnitud relativa de los componentes es una función de la frecuencia. Para ciertos productos frecuencia-espesor, la amplitud de un componente pasa por cero, de modo que el movimiento es completamente perpendicular o paralelo al plano de la placa. Para las partículas en la superficie de la placa, estas condiciones ocurren cuando la velocidad de fase de la onda Lamb es √ 2 c t o solo para modos simétricos c l , respectivamente. Estas consideraciones de direccionalidad son importantes cuando se considera la radiación de energía acústica desde las placas hacia los fluidos adyacentes.
El movimiento de las partículas también es completamente perpendicular o completamente paralelo al plano de la placa, en la frecuencia de nacimiento de un modo. Cerca de las frecuencias de nacimiento de los modos correspondientes a las resonancias de ondas longitudinales de la placa, su movimiento de partículas será casi completamente perpendicular al plano de la placa; y cerca de las resonancias de ondas transversales, paralelo.
J. y H. Krautkrämer han señalado [7] que las ondas Lamb pueden concebirse como un sistema de ondas longitudinales y transversales que se propagan en ángulos adecuados a lo largo y ancho de la placa. Estas ondas se reflejan, se transforman en modos y se combinan para producir un patrón de ondas coherente y sostenido. Para que se forme este patrón de ondas coherente, el espesor de la placa debe ser el adecuado en relación con los ángulos de propagación y las longitudes de onda de las ondas longitudinales y transversales subyacentes; este requisito conduce a las relaciones de dispersión de velocidad.
Si bien el análisis de Lamb suponía un frente de onda recto, se ha demostrado [8] que las mismas ecuaciones características se aplican a las ondas de placa cilíndricas (es decir, ondas que se propagan hacia afuera desde una fuente lineal, siendo la línea perpendicular a la placa). La diferencia es que mientras que la "portadora" para el frente de onda recto es una sinusoide, la "portadora" para la onda axisimétrica es una función de Bessel. La función de Bessel se ocupa de la singularidad en la fuente y luego converge hacia un comportamiento sinusoidal a grandes distancias.
Estas ondas cilíndricas son las funciones propias a partir de las cuales se puede componer la respuesta de la placa a perturbaciones puntuales. Por lo tanto, la respuesta de una placa a una perturbación puntual se puede expresar como una combinación de ondas Lamb, más términos evanescentes en el campo cercano. El resultado general se puede visualizar libremente como un patrón de frentes de onda circulares, como las ondulaciones de una piedra arrojada a un estanque, pero que cambian de forma más profundamente a medida que avanzan hacia afuera. La teoría de las ondas Lamb se relaciona únicamente con el movimiento en la dirección (r, z); el movimiento transversal es un tema diferente.
Esta frase se encuentra con bastante frecuencia en los ensayos no destructivos. Las "ondas Lamb guiadas" se pueden definir como ondas similares a las de Lamb que se guían por las dimensiones finitas de los objetos de prueba reales. Agregar el prefijo "guiadas" a la frase "onda Lamb" es reconocer que, en realidad, la placa infinita de Lamb no se encuentra en ninguna parte.
En realidad, tratamos con placas finitas, o placas envueltas en tubos o recipientes cilíndricos, o placas cortadas en tiras delgadas, etc. La teoría de las ondas Lamb a menudo da una muy buena explicación de gran parte del comportamiento ondulatorio de tales estructuras. No dará una explicación perfecta, y es por eso que la frase "Ondas Lamb Guiadas" es más relevante en la práctica que "Ondas Lamb". Una pregunta es cómo las velocidades y las formas modales de las ondas tipo Lamb se verán influenciadas por la geometría real de la pieza. Por ejemplo, la velocidad de una onda tipo Lamb en un cilindro delgado dependerá ligeramente del radio del cilindro y de si la onda se propaga a lo largo del eje o alrededor de la circunferencia. Otra pregunta es qué comportamientos acústicos y modos de onda completamente diferentes pueden estar presentes en la geometría real de la pieza. Por ejemplo, un tubo cilíndrico tiene modos de flexión asociados con el movimiento corporal de todo el tubo, bastante diferentes del modo de flexión tipo Lamb de la pared del tubo.
El objetivo de las pruebas ultrasónicas suele ser encontrar y caracterizar defectos individuales en el objeto que se está probando. Dichos defectos se detectan cuando reflejan o dispersan la onda incidente y la onda reflejada o dispersada llega a la unidad de búsqueda con suficiente amplitud.
Tradicionalmente, las pruebas ultrasónicas se han llevado a cabo con ondas cuya longitud de onda es mucho más corta que la dimensión de la pieza que se está inspeccionando. En este régimen de alta frecuencia, el inspector ultrasónico utiliza ondas que se aproximan a los modos de onda longitudinal y transversal de medio infinito, zigzagueando de un lado a otro del espesor de la placa. Aunque los pioneros de las ondas Lamb trabajaron en aplicaciones de pruebas no destructivas y llamaron la atención sobre la teoría, su uso generalizado no se produjo hasta la década de 1990, cuando los programas informáticos para calcular curvas de dispersión y relacionarlas con señales observables experimentalmente se hicieron mucho más accesibles. Estas herramientas computacionales, junto con una comprensión más generalizada de la naturaleza de las ondas Lamb, hicieron posible idear técnicas para pruebas no destructivas utilizando longitudes de onda que son comparables o mayores que el espesor de la placa. En estas longitudes de onda más largas, la atenuación de la onda es menor, por lo que los defectos se pueden detectar a mayores distancias.
Un desafío y una habilidad importantes en el uso de ondas Lamb para pruebas ultrasónicas es la generación de modos específicos a frecuencias específicas que se propaguen bien y den "ecos" de retorno limpios. Esto requiere un control cuidadoso de la excitación. Las técnicas para esto incluyen el uso de transductores de peine, cuñas, ondas de medios líquidos y transductores acústicos electromagnéticos ( EMAT ).
Las pruebas acústico-ultrasónicas difieren de las pruebas ultrasónicas en que fueron concebidas como un medio para evaluar los daños (y otros atributos del material) distribuidos en áreas importantes, en lugar de caracterizar los defectos individualmente. Las ondas Lamb son muy adecuadas para este concepto, porque irradian todo el espesor de la placa y se propagan a distancias importantes con patrones de movimiento consistentes.
La emisión acústica utiliza frecuencias mucho más bajas que las pruebas ultrasónicas tradicionales, y normalmente se espera que el sensor detecte fallas activas a distancias de hasta varios metros. Una gran fracción de las estructuras que se prueban habitualmente con emisión acústica están fabricadas con placas de acero: tanques, recipientes a presión, tuberías, etc. La teoría de ondas Lamb es, por lo tanto, la teoría principal para explicar las formas de señal y las velocidades de propagación que se observan al realizar pruebas de emisión acústica. El análisis de señales de emisión acústica mediante la teoría de ondas guiadas se conoce como emisión acústica modal (MAE). Se pueden lograr mejoras sustanciales en la precisión de la ubicación de la fuente (una técnica importante de las pruebas de EA) mediante una buena comprensión y una utilización hábil del conjunto de conocimientos de las ondas Lamb.
Una excitación mecánica arbitraria aplicada a una placa generará una multiplicidad de ondas Lamb que transportan energía a través de un rango de frecuencias. Tal es el caso de la onda de emisión acústica. En las pruebas de emisión acústica, el desafío es reconocer los múltiples componentes de la onda Lamb en la forma de onda recibida e interpretarlos en términos del movimiento de la fuente. Esto contrasta con la situación en las pruebas ultrasónicas, donde el primer desafío es generar un único modo de onda Lamb bien controlado en una única frecuencia. Pero incluso en las pruebas ultrasónicas, la conversión de modos se produce cuando la onda Lamb generada interactúa con los defectos, por lo que la interpretación de las señales reflejadas compuestas de múltiples modos se convierte en un medio de caracterización de los defectos.