Neurona artificial

Función matemática concebida como un modelo crudo

Estructura de una neurona artificial

Una neurona artificial es una función matemática concebida como un modelo de neuronas biológicas en una red neuronal . Las neuronas artificiales son las unidades elementales de las redes neuronales artificiales . ^[1] La neurona artificial es una función que recibe una o más entradas, aplica pesos a estas entradas y las suma para producir una salida.

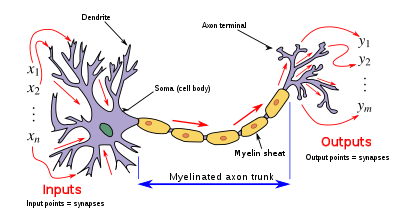
El diseño de la neurona artificial se inspiró en los circuitos neuronales . Sus entradas son análogas a los potenciales postsinápticos excitatorios y a los potenciales postsinápticos inhibidores en las dendritas neuronales , oactivación , sus pesos son análogos al peso sináptico y su salida es análoga al potencial de acción de una neurona que se transmite a lo largo de su axón .

Por lo general, cada entrada se pondera por separado y la suma se suele añadir a un término conocido como sesgo (que corresponde vagamente al potencial umbral ), antes de pasar por una función no lineal conocida como función de activación o función de transferencia ^{[ aclaración necesaria ]} . Las funciones de transferencia suelen tener forma sigmoidea , pero también pueden adoptar la forma de otras funciones no lineales, funciones lineales por partes o funciones escalonadas. También suelen ser monótonamente crecientes , continuas , diferenciables y acotadas . También se han explorado recientemente funciones de activación no monótonas, ilimitadas y oscilantes con múltiples ceros que superan a las funciones de activación sigmoideas y similares a ReLU en muchas tareas. La función de umbralización ha inspirado la construcción de puertas lógicas denominadas lógica de umbral; aplicable a la construcción de circuitos lógicos que se asemejan al procesamiento cerebral. Por ejemplo, en los últimos tiempos se han utilizado ampliamente nuevos dispositivos como los memristores para desarrollar dicha lógica. ^[2]

La función de transferencia de una neurona artificial no debe confundirse con la función de transferencia de un sistema lineal .

Una neurona artificial puede denominarse unidad semilineal , neurona Nv , neurona binaria , función umbral lineal o neurona McCulloch–Pitts ( MCP ) , según la estructura utilizada.

Las neuronas artificiales simples, como el modelo McCulloch-Pitts, a veces se describen como "modelos de caricatura", ya que pretenden reflejar una o más observaciones neurofisiológicas, pero sin tener en cuenta el realismo. ^[3] Las neuronas artificiales también pueden referirse a células artificiales en ingeniería neuromórfica ( ver más abajo ) que son similares a las neuronas físicas naturales.

Estructura básica

Para una neurona artificial k dada, sean m  + 1 entradas con señales x ₀ a x _m y pesos w _{k 0} a w _{k m} . Por lo general, a la entrada x ₀ se le asigna el valor +1, lo que la convierte en una entrada de sesgo con w _{k 0}  =  b _k . Esto deja solo m entradas reales a la neurona: de x ₁ a x _m .

La salida de la neurona k es:

${\displaystyle y_{k}=\varphi \left(\sum _{j=0}^{m}w_{kj}x_{j}\right)}$

Donde (phi) es la función de transferencia (comúnmente una función de umbral). ${\displaystyle \varphi }$

La salida es análoga al axón de una neurona biológica y su valor se propaga a la entrada de la siguiente capa, a través de una sinapsis. También puede salir del sistema, posiblemente como parte de un vector de salida .

No tiene un proceso de aprendizaje como tal. Sus pesos de función de transferencia están calculados y su valor umbral está predeterminado.

Neurona McCulloch-Pitts (MCP)

Una neurona MCP es un tipo de neurona artificial restringida que opera en pasos de tiempo discretos. Cada una tiene cero o más entradas, y se escriben como . Tiene una salida, escrita como . Cada entrada puede ser excitatoria o inhibidora . La salida puede ser tranquila o de activación . Una neurona MCP también tiene un umbral . ${\displaystyle x_{1},...,x_{n}}$ ${\displaystyle y}$ ${\displaystyle b\in \{0,1,2,...\}}$

En una red neuronal MCP, todas las neuronas funcionan en pasos de tiempo discretos sincrónicos de . En el momento , la salida de la neurona es si el número de entradas excitatorias activadas es al menos igual al umbral y no se activan entradas inhibidoras; en caso contrario. ${\displaystyle t=0,1,2,3,...}$ ${\displaystyle t+1}$ ${\displaystyle y(t+1)=1}$ ${\displaystyle y(t+1)=0}$

Cada salida puede ser la entrada de un número arbitrario de neuronas, incluida ella misma (es decir, son posibles los bucles propios). Sin embargo, una salida no puede conectarse más de una vez con una sola neurona. Los bucles propios no causan contradicciones, ya que la red opera en pasos de tiempo discretos sincrónicos.

Como ejemplo sencillo, considere una sola neurona con un umbral de 0 y un solo bucle inhibidor. Su salida oscilaría entre 0 y 1 en cada paso, actuando como un "reloj".

Cualquier máquina de estados finitos puede ser simulada por una red neuronal MCP. ^[4] Equipadas con una cinta infinita, las redes neuronales MCP pueden simular cualquier máquina de Turing . ^[5]

Modelos biológicos

Neurona y axón mielinizado, con flujo de señales desde las entradas en las dendritas hasta las salidas en las terminales del axón.

Las neuronas artificiales están diseñadas para imitar aspectos de sus contrapartes biológicas. Sin embargo, existe una brecha de rendimiento significativa entre las redes neuronales biológicas y artificiales. En particular, se han descubierto neuronas biológicas individuales en el cerebro humano con función de activación oscilante capaz de aprender la función XOR . ^[6]

• Dendritas : en una neurona biológica, las dendritas actúan como vector de entrada. Estas dendritas permiten que la célula reciba señales de una gran cantidad (>1000) de neuronas vecinas. Como en el tratamiento matemático anterior, cada dendrita puede realizar una "multiplicación" por el "valor de peso" de esa dendrita. La multiplicación se logra aumentando o disminuyendo la proporción de neurotransmisores sinápticos con respecto a las sustancias químicas de señalización introducidas en la dendrita en respuesta al neurotransmisor sináptico. Se puede lograr un efecto de multiplicación negativo transmitiendo inhibidores de señales (es decir, iones con carga opuesta) a lo largo de la dendrita en respuesta a la recepción de neurotransmisores sinápticos.
• Soma – En una neurona biológica, el soma actúa como función sumatoria, como se ve en la descripción matemática anterior. A medida que las señales positivas y negativas (excitantes e inhibidoras, respectivamente) llegan al soma desde las dendritas, los iones positivos y negativos se suman efectivamente, por el simple hecho de estar mezclados en la solución dentro del cuerpo celular.
• Axón : el axón recibe su señal del comportamiento de suma que ocurre dentro del soma. La apertura del axón básicamente toma una muestra del potencial eléctrico de la solución dentro del soma. Una vez que el soma alcanza un cierto potencial, el axón transmitirá un pulso de señal a lo largo de su longitud. En este sentido, el axón se comporta como la capacidad que tenemos para conectar nuestra neurona artificial con otras neuronas artificiales.

Sin embargo, a diferencia de la mayoría de las neuronas artificiales, las neuronas biológicas se activan en pulsos discretos. Cada vez que el potencial eléctrico dentro del soma alcanza un cierto umbral, se transmite un pulso a través del axón. Este pulso se puede traducir en valores continuos. La velocidad (activaciones por segundo, etc.) a la que se activa un axón se convierte directamente en la velocidad a la que se introducen iones de señal en las células vecinas. Cuanto más rápido se activa una neurona biológica, más rápido acumulan potencial eléctrico las neuronas cercanas (o lo pierden, dependiendo de la "ponderación" de la dendrita que se conecta a la neurona que se activó). Es esta conversión la que permite a los científicos informáticos y matemáticos simular redes neuronales biológicas utilizando neuronas artificiales que pueden generar valores distintos (a menudo de −1 a 1).

Codificación

Las investigaciones han demostrado que la codificación unaria se utiliza en los circuitos neuronales responsables de la producción del canto de los pájaros . ^{[7] [8]} El uso de la codificación unaria en redes biológicas se debe presumiblemente a la simplicidad inherente de la codificación. Otro factor que podría contribuir a ello es que la codificación unaria proporciona un cierto grado de corrección de errores. ^[9]

Células artificiales físicas

Se están realizando investigaciones y desarrollos en neuronas artificiales físicas, orgánicas e inorgánicas.

Por ejemplo, algunas neuronas artificiales pueden recibir ^{[10] [11]} y liberar dopamina ( señales químicas en lugar de señales eléctricas) y comunicarse con células cerebrales y musculares naturales de ratas , con potencial para su uso en BCI / prótesis . ^{[12] [13]}

Los memristores biocompatibles de bajo consumo pueden permitir la construcción de neuronas artificiales que funcionan a voltajes de potenciales de acción biológicos y podrían utilizarse para procesar directamente señales de biodetección , para computación neuromórfica y/o comunicación directa con neuronas biológicas . ^{[14] [15] [16]}

Se han incorporado circuitos neuromórficos orgánicos hechos de polímeros , recubiertos con un gel rico en iones para permitir que un material lleve una carga eléctrica como las neuronas reales , en un robot, lo que le permite aprender sensoriomotoramente dentro del mundo real, en lugar de a través de simulaciones o virtualmente. ^{[17] [18]} Además, las neuronas artificiales de punta hechas de materia blanda (polímeros) pueden operar en entornos biológicamente relevantes y permitir la comunicación sinérgica entre los dominios artificiales y biológicos. ^{[19] [20]}

Historia

La primera neurona artificial fue la Unidad Lógica de Umbral (TLU), o Unidad de Umbral Lineal, ^[21] propuesta por primera vez por Warren McCulloch y Walter Pitts en 1943 en Un cálculo lógico de las ideas inmanentes en la actividad nerviosa . El modelo fue específicamente diseñado como un modelo computacional de la "red nerviosa" en el cerebro. ^[22] Como función de transferencia, empleó un umbral, equivalente a usar la función de paso de Heaviside . Inicialmente, solo se consideró un modelo simple, con entradas y salidas binarias, algunas restricciones en los pesos posibles y un valor de umbral más flexible. Desde el principio ya se advirtió que cualquier función booleana podría implementarse mediante redes de tales dispositivos, lo que se ve fácilmente del hecho de que uno puede implementar las funciones AND y OR, y usarlas en la forma normal disyuntiva o conjuntiva . Los investigadores pronto se dieron cuenta también de que las redes cíclicas, con retroalimentaciones a través de neuronas, podían definir sistemas dinámicos con memoria, pero la mayor parte de la investigación se concentró (y todavía lo hace) en redes estrictamente de retroalimentación positiva debido a la menor dificultad que presentan.

Una red neuronal artificial importante y pionera que utilizó la función de umbral lineal fue el perceptrón , desarrollado por Frank Rosenblatt . Este modelo ya consideraba valores de peso más flexibles en las neuronas y se utilizaba en máquinas con capacidades adaptativas. La representación de los valores de umbral como un término de sesgo fue introducida por Bernard Widrow en 1960 – véase ADALINE .

A finales de los años 80, cuando la investigación sobre redes neuronales recobró fuerza, se empezaron a considerar neuronas con formas más continuas. La posibilidad de diferenciar la función de activación permite el uso directo del descenso de gradiente y otros algoritmos de optimización para el ajuste de los pesos. Las redes neuronales también empezaron a utilizarse como modelo de aproximación de funciones generales . El algoritmo de entrenamiento más conocido, llamado retropropagación, ha sido redescubierto varias veces, pero su primer desarrollo se remonta al trabajo de Paul Werbos . ^{[23] [24]}

Tipos de funciones de transferencia

La función de transferencia ( función de activación ) de una neurona se elige de modo que tenga una serie de propiedades que mejoren o simplifiquen la red que contiene la neurona. Por ejemplo, es crucial que cualquier perceptrón multicapa que utilice una función de transferencia lineal tenga una red monocapa equivalente; por lo tanto, es necesaria una función no lineal para obtener las ventajas de una red multicapa. ^{[ cita requerida ]}

A continuación, u se refiere en todos los casos a la suma ponderada de todas las entradas a la neurona, es decir, para n entradas,

${\displaystyle u=\sum _{i=1}^{n}w_{i}x_{i}}$

donde w es un vector de pesos sinápticos y x es un vector de entradas.

Función escalonada

La salida y de esta función de transferencia es binaria, dependiendo de si la entrada alcanza un umbral especificado, θ . La "señal" se envía, es decir, la salida se establece en uno, si la activación alcanza el umbral.

${\displaystyle y={\begin{cases}1&{\text{if }}u\geq \theta \\0&{\text{if }}u<\theta \end{cases}}}$

Esta función se utiliza en perceptrones y suele aparecer en muchos otros modelos. Realiza una división del espacio de entradas por un hiperplano . Es especialmente útil en la última capa de una red destinada a realizar una clasificación binaria de las entradas. Se puede aproximar a partir de otras funciones sigmoideas asignando valores grandes a los pesos.

Combinación lineal

En este caso, la unidad de salida es simplemente la suma ponderada de sus entradas más un término de sesgo . Un número de estas neuronas lineales realizan una transformación lineal del vector de entrada. Esto suele ser más útil en las primeras capas de una red. Existe una serie de herramientas de análisis basadas en modelos lineales, como el análisis armónico , y todas ellas se pueden utilizar en redes neuronales con esta neurona lineal. El término de sesgo nos permite realizar transformaciones afines a los datos.

Ver: Transformación lineal , Análisis armónico , Filtro lineal , Wavelet , Análisis de componentes principales , Análisis de componentes independientes , Deconvolución .

Sigmoideo

Una función no lineal bastante simple, la función sigmoidea, como la función logística, también tiene una derivada fácil de calcular, que puede ser importante al calcular las actualizaciones de peso en la red. Por lo tanto, hace que la red sea más fácil de manipular matemáticamente y fue atractiva para los primeros científicos informáticos que necesitaban minimizar la carga computacional de sus simulaciones. Anteriormente se veía comúnmente en perceptrones multicapa . Sin embargo, trabajos recientes han demostrado que las neuronas sigmoideas son menos efectivas que las neuronas lineales rectificadas . La razón es que los gradientes calculados por el algoritmo de retropropagación tienden a disminuir hacia cero a medida que las activaciones se propagan a través de capas de neuronas sigmoideas, lo que dificulta la optimización de las redes neuronales utilizando múltiples capas de neuronas sigmoideas.

Rectificador

En el contexto de las redes neuronales artificiales , el rectificador o ReLU (Rectified Linear Unit) es una función de activación definida como la parte positiva de su argumento:

${\displaystyle f(x)=x^{+}=\max(0,x),}$

donde x es la entrada a una neurona. Esto también se conoce como función de rampa y es análoga a la rectificación de media onda en ingeniería eléctrica. Esta función de activación fue introducida por primera vez a una red dinámica por Hahnloser et al. en un artículo de 2000 en Nature ^[25] con fuertes motivaciones biológicas y justificaciones matemáticas. ^[26] Se ha demostrado por primera vez en 2011 que permite un mejor entrenamiento de redes más profundas, ^[27] en comparación con las funciones de activación ampliamente utilizadas antes de 2011, es decir, la sigmoidea logística (que está inspirada en la teoría de la probabilidad ; consulte regresión logística ) y su contraparte más práctica ^{[28] , la} tangente hiperbólica .

Una variante comúnmente utilizada de la función de activación ReLU es Leaky ReLU, que permite un pequeño gradiente positivo cuando la unidad no está activa:

${\displaystyle f(x)={\begin{cases}x&{\text{if }}x>0,\\ax&{\text{otherwise}}.\end{cases}}}$

donde x es la entrada a la neurona y a es una pequeña constante positiva (en el artículo original se utilizó el valor 0,01 para a ). ^[29]

Algoritmo de pseudocódigo

La siguiente es una implementación de pseudocódigo simple ^{[ cita requerida ]} de una única TLU que toma entradas booleanas (verdadero o falso) y devuelve una única salida booleana cuando se activa. Se utiliza un modelo orientado a objetos . No se define ningún método de entrenamiento, ya que existen varios. Si se utilizara un modelo puramente funcional, la TLU de clase a continuación se reemplazaría con una TLU de función con parámetros de entrada umbral, pesos y entradas que devolvieran un valor booleano.

Clase TLU definida como: umbral de miembro de datos : número pesos de miembro de datos : lista de números de tamaño X miembro de función fire(inputs : lista de booleanos de tamaño X) : booleano definido como:  variable T : número T ← 0 para cada i en 1 a X hacer  si entradas(i) es verdadero entonces T ← T + pesos(i) fin si  fin para cada  si T > umbral entonces  devuelve verdadero de lo contrario:  devuelve falso fin si  fin de la función fin de la clase

Véase también

• Neurona de enlace
• Conexionismo

Referencias

1. Rami A. Alzahrani; Alice C. Parker. "Circuitos neuromórficos con modulación neuronal que mejoran el contenido de información de la señalización neuronal". Actas de la Conferencia internacional sobre sistemas neuromórficos 2020. Arte. 19. Nueva York: Association for Computing Machinery. doi : 10.1145/3407197.3407204 . ISBN. 978-1-4503-8851-1. Número de identificación del sujeto  220794387.
2. Maan, AK; Jayadevi, DA; James, AP (1 de enero de 2016). "Un estudio de circuitos lógicos de umbral memristivos". IEEE Transactions on Neural Networks and Learning Systems . PP (99): 1734–1746. arXiv : 1604.07121 . Bibcode :2016arXiv160407121M. doi :10.1109/TNNLS.2016.2547842. ISSN  2162-237X. PMID  27164608. S2CID  1798273.
3. FC Hoppensteadt y EM Izhikevich (1997). Redes neuronales débilmente conectadas . Springer. pág. 4. ISBN 978-0-387-94948-2.
4. Minsky, Marvin Lee (1 de enero de 1967). Computación: máquinas finitas e infinitas . Prentice Hall. ISBN 978-0-13-165563-8.
5. McCulloch, Warren S.; Pitts, Walter (1943-12-01). "Un cálculo lógico de las ideas inmanentes en la actividad nerviosa". Boletín de Biofísica Matemática . 5 (4): 115–133. doi :10.1007/BF02478259. ISSN  1522-9602.
6. Gidón, Albert; Zolnik, Timothy Adam; Fidzinski, Pawel; Bolduán, Félix; Papoutsi, Atanasia; Poirazi, Panayiota ; Holtkamp, ​​Martín; Vida, Imre; Larkum, Matthew Evan (3 de enero de 2020). "Potenciales de acción dendríticas y computación en neuronas corticales de la capa 2/3 humana". Ciencia . 367 (6473): 83–87. Código Bib : 2020 Ciencia... 367... 83G. doi : 10.1126/ciencia.aax6239 . PMID  31896716. S2CID  209676937.
7. Squire, L.; Albright, T.; Bloom, F.; Gage, F.; Spitzer, N., eds. (octubre de 2007). Modelos de redes neuronales de producción, aprendizaje y codificación del canto de las aves (PDF) . Nueva enciclopedia de neurociencia: Elservier. Archivado desde el original (PDF) el 12 de abril de 2015 . Consultado el 12 de abril de 2015 .
8. Moore, JM; et al. (2011). "La convergencia de la vía motora predice el tamaño del repertorio de sílabas en aves oscinas". Proc. Natl. Sci. USA . 108 (39): 16440–16445. Bibcode :2011PNAS..10816440M. doi : 10.1073/pnas.1102077108 . PMC 3182746 . PMID  21918109. 
9. Potluri, Pushpa Sree (26 de noviembre de 2014). "Capacidad de corrección de errores de la codificación unaria". arXiv : 1411.7406 [cs.IT].
10. Kleiner, Kurt (25 de agosto de 2022). «Hacer que los chips de ordenador actúen más como células cerebrales». Revista Knowable | Reseñas anuales . doi :10.1146/knowable-082422-1 . Consultado el 23 de septiembre de 2022 .
11. Keene, Scott T.; Lubrano, Claudia; Kazemzadeh, Setareh; Melianas, Armantas; Tuchman, Yaakov; Polino, Giuseppina; Scognamiglio, Paola; Ciná, Lucio; Salleo, Alberto; van de Burgt, Yoeri; Santoro, Francesca (septiembre de 2020). "Una sinapsis biohíbrida con plasticidad mediada por neurotransmisores". Materiales de la naturaleza . 19 (9): 969–973. Código Bib : 2020NatMa..19..969K. doi :10.1038/s41563-020-0703-y. ISSN  1476-4660. PMID  32541935. S2CID  219691307.
    • Nota de prensa de la universidad: «Los investigadores desarrollan una sinapsis artificial que funciona con células vivas». Universidad de Stanford a través de medicalxpress.com . Consultado el 23 de septiembre de 2022 .
12. "Una neurona artificial intercambia dopamina con células cerebrales de rata como una real". New Scientist . Consultado el 16 de septiembre de 2022 .
13. Wang, Ting; Wang, Ming; Wang, Jianwu; Yang, Le; Ren, Xueyang; Canción, pandilla; Chen, Shisheng; Yuan, Yuehui; Liu, Ruiqing; Pan, Liang; Li, Zheng; Leow, Wan Ru; Luo, Yifei; Ji, Shaobo; Cui, Zequán; Él, Ke; Zhang, Fei Long; Lv, Fengting; Tian, ​​Yuanyuan; Cai, Kaiyu; Yang, Bowen; Niu, Jingyi; Zou, Haochen; Liu, Songrui; Xu, Guoliang; Fan, Xing; Hu, Benhui; Loh, Xian Jun; Wang, Lianhui; Chen, Xiaodong (8 de agosto de 2022). "Una neurona artificial mediada químicamente" . Electrónica de la naturaleza . 5 (9): 586–595. doi :10.1038/s41928-022-00803-0. hdl : 10356/163240 . ISSN  2520-1131. S2CID  251464760.
14. "Los científicos crean pequeños dispositivos que funcionan como el cerebro humano". The Independent . 20 de abril de 2020. Archivado desde el original el 24 de abril de 2020 . Consultado el 17 de mayo de 2020 .
15. "Investigadores descubren dispositivos electrónicos que imitan el cerebro humano para un aprendizaje eficiente". phys.org . Archivado desde el original el 28 de mayo de 2020 . Consultado el 17 de mayo de 2020 .
16. Fu, Tianda; Liu, Xiaomeng; Gao, Hongyan; Ward, alegría E.; Liu, Xiaorong; Yin, Bing; Wang, Zhongrui; Zhuo, Ye; Walker, David JF; Josué Yang, J.; Chen, Jianhan; Loveley, Derek R.; Yao, junio (20 de abril de 2020). "Memristores de biovoltaje bioinspirados". Comunicaciones de la naturaleza . 11 (1): 1861. Bibcode : 2020NatCo..11.1861F. doi : 10.1038/s41467-020-15759-y . PMC 7171104 . PMID  32313096. 
17. Bolakhe, Saugat. «Un robot Lego con un 'cerebro' orgánico aprende a navegar por un laberinto». Scientific American . Consultado el 1 de febrero de 2022 .
18. Krauhausen, Imke; Koutsouras, Dimitrios A.; Melianas, Armantas; Keene, Scott T.; Lieberth, Katharina; Ledanseur, Hadrien; Sheelamanthula, Rajendar; Giovannitti, Alejandro; Torricelli, Fabricio; Mcculloch, Iain; Blom, Paul WM; Salleo, Alberto; Burgt, Yoeri van de; Gkoupidenis, Paschalis (diciembre de 2021). "Electrónica neuromórfica orgánica para la integración y el aprendizaje sensoriomotor en robótica". Avances científicos . 7 (50): eabl5068. Código Bib : 2021SciA....7.5068K. doi :10.1126/sciadv.abl5068. hdl : 10754/673986. PMC 8664264 . Número de modelo: PMID  34890232. Número de modelo: S2CID  245046482. 
19. Sarkar, Tanmoy; Lieberth, Katharina; Pavlou, Aristea; Franco, Tomás; Mailaender, Volker; McCulloch, Iain; Blom, Paul WM; Torriccelli, Fabrizio; Gkoupidenis, Paschalis (7 de noviembre de 2022). "Una neurona artificial orgánica para detección neuromórfica in situ y biointerconexión". Electrónica de la naturaleza . 5 (11): 774–783. doi : 10.1038/s41928-022-00859-y . hdl : 10754/686016 . ISSN  2520-1131. S2CID  253413801.
20. "Las neuronas artificiales emulan a sus homólogas biológicas para permitir un funcionamiento sinérgico". Nature Electronics . 5 (11): 721–722. 10 de noviembre de 2022. doi :10.1038/s41928-022-00862-3. ISSN  2520-1131. S2CID  253469402.
21. Martin Anthony (enero de 2001). Matemática discreta de redes neuronales: temas seleccionados. SIAM. pp. 3–. ISBN 978-0-89871-480-7.
22. Charu C. Aggarwal (25 de julio de 2014). Clasificación de datos: algoritmos y aplicaciones. CRC Press. pp. 209–. ISBN 978-1-4665-8674-1.
23. Paul Werbos , Más allá de la regresión: nuevas herramientas para la predicción y el análisis en las ciencias del comportamiento. Tesis doctoral, Universidad de Harvard, 1974
24. Werbos, PJ (1990). "Retropropagación a través del tiempo: qué hace y cómo hacerlo". Actas del IEEE . 78 (10): 1550–1560. doi :10.1109/5.58337. ISSN  0018-9219. S2CID  18470994.
25. Hahnloser, Richard HR; Sarpeshkar, Rahul; Mahowald, Misha A.; Douglas, Rodney J.; Seung, H. Sebastian (2000). "La selección digital y la amplificación analógica coexisten en un circuito de silicio inspirado en la corteza". Nature . 405 (6789): 947–951. Bibcode :2000Natur.405..947H. doi :10.1038/35016072. ISSN  0028-0836. PMID  10879535. S2CID  4399014.
26. R Hahnloser; HS Seung (2001). Conjuntos permitidos y prohibidos en redes lineales de umbral simétrico . NIPS 2001.
27. Xavier Glorot; Antoine Bordes; Yoshua Bengio (2011). Redes neuronales rectificadoras dispersas profundas (PDF) . AISTATS.
28. Yann LeCun ; Leon Bottou ; Genevieve B. Orr; Klaus-Robert Müller (1998). "BackProp eficiente" (PDF) . En G. Orr; K. Müller (eds.). Redes neuronales: trucos del oficio . Springer.
29. Andrew L. Maas, Awni Y. Hannun, Andrew Y. Ng (2014). Las no linealidades del rectificador mejoran los modelos acústicos de redes neuronales.

Lectura adicional

• McCulloch, Warren S. ; Pitts, Walter (1943). "Un cálculo lógico de las ideas inmanentes en la actividad nerviosa". Boletín de biofísica matemática . 5 (4): 115–133. doi :10.1007/bf02478259.
• Samardak, A.; Nogaret, A.; Janson, NB; Balanov, AG; Farrer, I.; Ritchie, DA (5 de junio de 2009). "Transmisión de señales controladas por ruido en una neurona semiconductora multihilo". Physical Review Letters . 102 (22): 226802. Bibcode :2009PhRvL.102v6802S. doi :10.1103/physrevlett.102.226802. PMID  19658886. S2CID  11211062.

Enlaces externos

• Una neurona artificial imita la función de las células humanas
• Neuronas McCulloch-Pitts (descripción general)