Órbita de transferencia de Hohmann

Maniobra de transferencia entre dos órbitas

Órbita de transferencia de Hohmann, denominada 2, desde una órbita (1) a una órbita superior (3)

Un ejemplo de una órbita de transferencia de Hohmann entre la Tierra y Marte, como la utilizada por la sonda InSight de la NASA :
   Conocimiento  ·   Tierra  ·   Marte

En astronáutica , la órbita de transferencia de Hohmann ( /ˈh oʊm ən / ) es una maniobra orbital utilizada para transferir una nave espacial entre dos órbitas de diferentes altitudes alrededor de un cuerpo central. Por ejemplo, una transferencia de Hohmann podría usarse para elevar la órbita de un satélite desde la órbita terrestre baja a la órbita geoestacionaria . En el caso idealizado, las órbitas inicial y objetivo son circulares y coplanares . La maniobra se logra colocando la nave en una órbita de transferencia elíptica que es tangencial tanto a la órbita inicial como a la objetivo. La maniobra utiliza dos quemas impulsivas del motor: la primera establece la órbita de transferencia y la segunda ajusta la órbita para que coincida con el objetivo.

La maniobra de Hohmann suele utilizar la menor cantidad posible de impulso (que consume una cantidad proporcional de delta-v y, por lo tanto, de propulsor ) para lograr la transferencia, pero requiere un tiempo de viaje relativamente más largo que las transferencias con mayor impulso. En algunos casos en los que una órbita es mucho más grande que la otra, una transferencia bielíptica puede utilizar incluso menos impulso, a costa de un tiempo de viaje aún mayor.

La maniobra debe su nombre a Walter Hohmann , el científico alemán que publicó una descripción de ella en su libro de 1925 Die Erreichbarkeit der Himmelskörper ( La alcanzabilidad de los cuerpos celestes ). ^[1] Hohmann estuvo influenciado en parte por el autor de ciencia ficción alemán Kurd Lasswitz y su libro de 1897 Dos planetas .

Cuando se utiliza para viajar entre cuerpos celestes, una órbita de transferencia de Hohmann requiere que los puntos de partida y destino estén en ubicaciones particulares en sus órbitas relativas entre sí. Las misiones espaciales que utilizan una transferencia de Hohmann deben esperar a que se produzca esta alineación requerida, lo que abre una ventana de lanzamiento . Para una misión entre la Tierra y Marte , por ejemplo, estas ventanas de lanzamiento ocurren cada 26 meses. Una órbita de transferencia de Hohmann también determina un tiempo fijo necesario para viajar entre los puntos de partida y destino; para un viaje Tierra-Marte, este tiempo de viaje es de unos 9 meses. Cuando la transferencia se realiza entre órbitas cercanas a cuerpos celestes con una gravitación significativa, normalmente se requiere mucho menos delta-v , ya que se puede emplear el efecto Oberth para las quemaduras.

También se utilizan a menudo para estas situaciones, pero las transferencias de baja energía que tienen en cuenta las limitaciones de empuje de los motores reales y aprovechan los pozos de gravedad de ambos planetas pueden ser más eficientes en términos de combustible. ^{[2] [3] [4]}

Ejemplo

El diagrama muestra una órbita de transferencia de Hohmann para llevar una nave espacial desde una órbita circular inferior a una superior. Es una órbita elíptica que es tangencial tanto a la órbita circular inferior que la nave espacial debe abandonar (cian, marcada con el 1 en el diagrama) como a la órbita circular superior que debe alcanzar (rojo, marcada con el 3 en el diagrama). La órbita de transferencia (amarilla, marcada con el 2 en el diagrama) se inicia encendiendo el motor de la nave espacial para agregar energía y elevar el apogeo . Cuando la nave espacial alcanza el apogeo, el encendido de un segundo motor agrega energía para elevar el perigeo, colocando la nave espacial en la órbita circular más grande.

Debido a la reversibilidad de las órbitas , se puede utilizar una órbita de transferencia de Hohmann similar para llevar una nave espacial desde una órbita más alta a una más baja; en este caso, el motor de la nave espacial se enciende en la dirección opuesta a su trayectoria actual, desacelerando la nave espacial y bajando su perigeo al de la órbita de transferencia elíptica. Luego, el motor se enciende nuevamente a la distancia más baja para desacelerar la nave espacial a la órbita circular más baja. La órbita de transferencia de Hohmann se basa en dos cambios de velocidad instantáneos . Se requiere combustible adicional para compensar el hecho de que las ráfagas toman tiempo; esto se minimiza utilizando motores de alto empuje para minimizar la duración de las ráfagas. Para las transferencias en órbita terrestre, los dos encendidos se etiquetan como encendido de perigeo y encendido de apogeo (o patada de apogeo ^[5] ); de manera más general, se etiquetan como quemaduras de periapsis y apoapsis . Alternativamente, el segundo encendido para circularizar la órbita puede denominarse encendido de circularización .

Tipo I y Tipo II

Una órbita de transferencia de Hohmann ideal se desplaza entre dos órbitas circulares en el mismo plano y recorre exactamente 180° alrededor de la primaria. En el mundo real, la órbita de destino puede no ser circular y no ser coplanar con la órbita inicial. Las órbitas de transferencia del mundo real pueden recorrer un poco más o un poco menos de 180° alrededor de la primaria. Una órbita que recorre menos de 180° alrededor de la primaria se denomina transferencia de Hohmann de "Tipo I", mientras que una órbita que recorre más de 180° se denomina transferencia de Hohmann de "Tipo II". ^{[6] [7]}

Las órbitas de transferencia pueden recorrer más de 360° alrededor del núcleo primario. Estas transferencias de múltiples revoluciones a veces se denominan Tipo III y Tipo IV, donde un Tipo III es un Tipo I más 360°, y un Tipo IV es un Tipo II más 360°. ^[8]

Usos

Una órbita de transferencia de Hohmann se puede utilizar para transferir la órbita de un objeto hacia otro objeto, siempre que coorbiten un cuerpo más masivo. En el contexto de la Tierra y el Sistema Solar , esto incluye cualquier objeto que orbite alrededor del Sol . Un ejemplo de dónde se podría utilizar una órbita de transferencia de Hohmann es para poner un asteroide, que orbita alrededor del Sol, en contacto con la Tierra. ^[9]

Cálculo

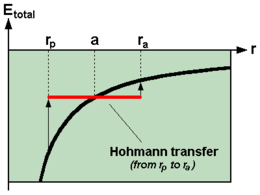
Para un cuerpo pequeño que orbita alrededor de otro cuerpo mucho más grande, como un satélite que orbita la Tierra, la energía total del cuerpo más pequeño es la suma de su energía cinética y su energía potencial , y esta energía total también es igual a la mitad de la energía potencial a la distancia promedio (el semieje mayor ): ${\displaystyle a}$ $${\displaystyle E={\frac {mv^{2}}{2}}-{\frac {GMm}{r}}={\frac {-GMm}{2a}}.}$$

Resolviendo esta ecuación para la velocidad se obtiene la ecuación vis-viva , donde: $${\displaystyle v^{2}=\mu \left({\frac {2}{r}}-{\frac {1}{a}}\right),}$$

• ${\displaystyle v}$es la velocidad de un cuerpo en órbita,
• ${\displaystyle \mu =GM}$es el parámetro gravitacional estándar del cuerpo primario, asumiendo que no es significativamente mayor que (lo que hace ), (para la Tierra, esto es μ ~3.986E14 m ³ s ⁻² ) ${\displaystyle M+m}$ ${\displaystyle M}$ ${\displaystyle v_{M}\ll v}$
• ${\displaystyle r}$es la distancia del cuerpo en órbita desde el foco primario,
• ${\displaystyle a}$es el semieje mayor de la órbita del cuerpo.

Por lo tanto, el delta- v (Δv) requerido para la transferencia de Hohmann se puede calcular de la siguiente manera, bajo el supuesto de impulsos instantáneos: para entrar en la órbita elíptica en desde la órbita circular, donde es el afelio de la órbita elíptica resultante, y para salir de la órbita elíptica en hasta la órbita circular, donde y son respectivamente los radios de las órbitas circulares de salida y llegada; el menor (mayor) de y corresponde a la distancia de periapsis ( distancia de apoapsis ) de la órbita de transferencia elíptica de Hohmann. Normalmente, se da en unidades de m ³ /s ² , por lo que asegúrese de utilizar metros, no kilómetros, para y . El total es entonces: $${\displaystyle \Delta v_{1}={\sqrt {\frac {\mu }{r_{1}}}}\left({\sqrt {\frac {2r_{2}}{r_{1}+r_{2}}}}-1\right),}$$ ${\displaystyle r=r_{1}}$ ${\displaystyle r_{1}}$ ${\displaystyle r_{2}}$ $${\displaystyle \Delta v_{2}={\sqrt {\frac {\mu }{r_{2}}}}\left(1-{\sqrt {\frac {2r_{1}}{r_{1}+r_{2}}}}\right),}$$ ${\displaystyle r=r_{2}}$ ${\displaystyle r_{2}}$ ${\displaystyle r_{1}}$ ${\displaystyle r_{2}}$ ${\displaystyle r_{1}}$ ${\displaystyle r_{2}}$ ${\displaystyle \mu }$ ${\displaystyle r_{1}}$ ${\displaystyle r_{2}}$ ${\displaystyle \Delta v}$

$${\displaystyle \Delta v_{\text{total}}=\Delta v_{1}+\Delta v_{2}.}$$

Ya sea que se mueva a una órbita más alta o más baja, según la tercera ley de Kepler ^{[ ancla rota ]} , el tiempo que toma transferirse entre las órbitas es

$${\displaystyle t_{\text{H}}={\frac {1}{2}}{\sqrt {\frac {4\pi ^{2}a_{\text{H}}^{3}}{\mu }}}=\pi {\sqrt {\frac {(r_{1}+r_{2})^{3}}{8\mu }}}}$$(la mitad del período orbital de toda la elipse), donde es la longitud del semieje mayor de la órbita de transferencia de Hohmann. ${\displaystyle a_{\text{H}}}$

En la aplicación del desplazamiento de un cuerpo celeste a otro, es fundamental iniciar la maniobra en el momento en que los dos cuerpos estén correctamente alineados. Teniendo en cuenta que la velocidad angular objetivo es la alineación angular α (en radianes ) en el momento del inicio entre el objeto de origen y el objeto de destino, se deberá $${\displaystyle \omega _{2}={\sqrt {\frac {\mu }{r_{2}^{3}}}},}$$ $${\displaystyle \alpha =\pi -\omega _{2}t_{\text{H}}=\pi \left(1-{\frac {1}{2{\sqrt {2}}}}{\sqrt {\left({\frac {r_{1}}{r_{2}}}+1\right)^{3}}}\right).}$$

Ejemplo

Balance total de energía durante una transferencia de Hohmann entre dos órbitas circulares con primer radio y segundo radio ${\displaystyle r_{p}}$ ${\displaystyle r_{a}}$

Considérese una órbita de transferencia geoestacionaria , que comienza en r ₁ = 6.678 km (altitud 300 km) y termina en una órbita geoestacionaria con r ₂ = 42.164 km (altitud 35.786 km).

En la órbita circular más pequeña la velocidad es de 7,73 km/s; en la más grande, de 3,07 km/s. En la órbita elíptica intermedia la velocidad varía de 10,15 km/s en el perigeo a 1,61 km/s en el apogeo.

Por lo tanto, el Δv para el primer encendido es 10,15 − 7,73 = 2,42 km/s, para el segundo encendido 3,07 − 1,61 = 1,46 km/s, y para ambos juntos 3,88 km/s.

Esto es mayor que el Δv requerido para una órbita de escape : 10,93 − 7,73 = 3,20 km/s. Aplicar un Δv en la órbita terrestre baja (LEO) de solo 0,78 km/s más (3,20−2,42) daría al cohete la velocidad de escape , que es menor que el Δv de 1,46 km/s requerido para circularizar la órbita geosincrónica. Esto ilustra el efecto Oberth de que a grandes velocidades el mismo Δv proporciona más energía orbital específica , y el aumento de energía se maximiza si uno gasta el Δv lo más rápido posible, en lugar de gastar algo, ser desacelerado por la gravedad y luego gastar algo más para superar la desaceleración (por supuesto, el objetivo de una órbita de transferencia de Hohmann es diferente).

En el peor de los casos, delta máximoen

Como demuestra el ejemplo anterior, el Δ v requerido para realizar una transferencia de Hohmann entre dos órbitas circulares no es el mayor cuando el radio de destino es infinito. (La velocidad de escape es √ 2 veces la velocidad orbital, por lo que el Δv requerido para escapar es √ 2  − 1 (41,4 %) de la velocidad orbital). El Δv requerido es mayor (53,0 % de la velocidad orbital más pequeña) cuando el radio de la órbita más grande es 15,5817... veces el de la órbita más pequeña. ^[10] Este número es la raíz positiva de x ³ − 15 x ² − 9 x − 1 = 0 , que es . Para relaciones de órbita más altas, el Δ v requerido para la segunda quema disminuye más rápido de lo que aumenta la primera. ${\textstyle 5+4\,{\sqrt {7}}\cos \left({1 \over 3}\arctan {{\sqrt {3}} \over 37}\right)}$

Aplicación a los viajes interplanetarios

Cuando se utiliza para mover una nave espacial desde la órbita de un planeta a la órbita de otro, el efecto Oberth permite utilizar menos delta- v que la suma de los delta- v para maniobras separadas para escapar del primer planeta, seguido de una transferencia de Hohmann al segundo planeta, seguida de la inserción en una órbita alrededor del otro planeta.

Por ejemplo, considere una nave espacial que viaja de la Tierra a Marte . Al comienzo de su viaje, la nave espacial ya tendrá una cierta velocidad y energía cinética asociada con su órbita alrededor de la Tierra. Durante el encendido, el motor del cohete aplica su delta- v , pero la energía cinética aumenta como una ley cuadrada, hasta que es suficiente para escapar del potencial gravitatorio del planeta , y luego quema más para ganar suficiente energía para entrar en la órbita de transferencia de Hohmann (alrededor del Sol ). Debido a que el motor del cohete puede hacer uso de la energía cinética inicial del propulsor, se requiere mucho menos delta- v por encima de lo necesario para alcanzar la velocidad de escape, y la situación óptima es cuando el encendido de transferencia se realiza a una altitud mínima ( periapsis baja ) sobre el planeta. El delta- v necesario es solo de 3,6 km/s, solo unos 0,4 km/s más de lo necesario para escapar de la Tierra, aunque esto da como resultado que la nave espacial vaya 2,9 km/s más rápido que la Tierra mientras se dirige a Marte (ver tabla a continuación).

En el otro extremo, la nave espacial debe desacelerar para que la gravedad de Marte la capture. Lo mejor es que esta combustión de captura se realice a baja altitud para aprovechar al máximo el efecto Oberth. Por lo tanto, se necesitan cantidades relativamente pequeñas de empuje en ambos extremos del viaje para organizar la transferencia en comparación con la situación en el espacio libre.

Sin embargo, en cualquier transferencia de Hohmann, la alineación de los dos planetas en sus órbitas es crucial: el planeta de destino y la nave espacial deben llegar al mismo punto en sus respectivas órbitas alrededor del Sol al mismo tiempo. Este requisito de alineación da lugar al concepto de ventanas de lanzamiento .

El término órbita de transferencia lunar (LTO) se utiliza para la Luna .

Es posible aplicar la fórmula dada anteriormente para calcular el Δv en km/s necesario para entrar en una órbita de transferencia de Hohmann y llegar a varios destinos desde la Tierra (suponiendo órbitas circulares para los planetas). En esta tabla, la columna etiquetada "Δv para entrar en la órbita de Hohmann desde la órbita de la Tierra" da el cambio de la velocidad de la Tierra a la velocidad necesaria para llegar a una elipse de Hohmann cuyo otro extremo estará a la distancia deseada del Sol. La columna etiquetada "altura LEO" da la velocidad necesaria (en un marco de referencia no giratorio centrado en la Tierra) a 300 km sobre la superficie de la Tierra. Esto se obtiene añadiendo a la energía cinética específica el cuadrado de la velocidad de escape (10,9 km/s) desde esta altura. La columna "LEO" es simplemente la velocidad anterior menos la velocidad orbital LEO de 7,73 km/s.

Téngase en cuenta que en la mayoría de los casos, Δ v desde LEO es menor que Δ v para entrar en la órbita de Hohmann desde la órbita de la Tierra.

Para llegar al Sol, en realidad no es necesario utilizar un Δ v de 24 km/s. Se pueden utilizar 8,8 km/s para alejarse mucho del Sol, luego utilizar un Δ v despreciable para llevar el momento angular a cero y luego caer al Sol. Esto puede considerarse una secuencia de dos transferencias de Hohmann, una hacia arriba y otra hacia abajo. Además, la tabla no proporciona los valores que se aplicarían al utilizar la Luna como asistencia gravitatoria . También existen posibilidades de utilizar un planeta, como Venus, que es el más fácil de alcanzar, para ayudar a llegar a otros planetas o al Sol.

Comparación con otras transferencias

Transferencia bielíptica

La transferencia bielíptica consta de dos órbitas semielípticas . Desde la órbita inicial, un primer encendido gasta delta-v para impulsar la nave espacial a la primera órbita de transferencia con un apoápside en algún punto alejado del cuerpo central . En este punto, un segundo encendido envía la nave espacial a la segunda órbita elíptica con periápside en el radio de la órbita final deseada, donde se realiza un tercer encendido, inyectando la nave espacial en la órbita deseada. ^[11] ${\displaystyle r_{b}}$

Si bien requieren una quema de motor más que una transferencia Hohmann y generalmente requieren un mayor tiempo de viaje, algunas transferencias bielípticas requieren una cantidad menor de delta-v total que una transferencia Hohmann cuando la relación entre el semieje mayor final y el inicial es 11,94 o mayor, dependiendo del semieje mayor intermedio elegido. ^[12]

La idea de la trayectoria de transferencia bielíptica fue publicada por primera vez ^{[ cita requerida ] por} Ary Sternfeld en 1934. ^[13]

Transferencia de bajo empuje

Los motores de bajo empuje pueden realizar una aproximación a una órbita de transferencia de Hohmann, creando una ampliación gradual de la órbita circular inicial mediante encendidos del motor cuidadosamente sincronizados. Esto requiere un cambio en la velocidad (delta- v ) que es mayor que la órbita de transferencia de dos impulsos ^[14] y tarda más en completarse.

Los motores como los propulsores iónicos son más difíciles de analizar con el modelo delta- v . Estos motores ofrecen un empuje muy bajo y, al mismo tiempo, un presupuesto delta- v mucho mayor, un impulso específico mucho mayor y una menor masa de combustible y motor. Una maniobra de transferencia Hohmann de dos quemadores sería poco práctica con un empuje tan bajo; la maniobra optimiza principalmente el uso de combustible, pero en esta situación hay relativamente suficiente.

Si en una misión solo se planean maniobras de bajo empuje, entonces el encendido continuo de un motor de bajo empuje, pero de muy alta eficiencia, podría generar un delta- v más alto y al mismo tiempo utilizar menos propulsor que un motor de cohete químico convencional.

Pasar de una órbita circular a otra cambiando gradualmente el radio simplemente requiere el mismo delta- v que la diferencia entre las dos velocidades. ^[14] Tal maniobra requiere más delta- v que una maniobra de transferencia Hohmann de 2 quemaduras, pero lo hace con un empuje bajo continuo en lugar de aplicaciones cortas de empuje alto.

La cantidad de masa propulsora utilizada mide la eficiencia de la maniobra más el hardware empleado para ello. El delta- v total utilizado mide únicamente la eficiencia de la maniobra. En el caso de los sistemas de propulsión eléctrica , que tienden a tener un empuje bajo, la alta eficiencia del sistema propulsor generalmente compensa el delta-V más alto en comparación con la maniobra de Hohmann, que es más eficiente.

Las órbitas de transferencia que utilizan propulsión eléctrica o motores de bajo empuje optimizan el tiempo de transferencia para alcanzar la órbita final y no la delta-v como en la órbita de transferencia de Hohmann. En el caso de la órbita geoestacionaria, la órbita inicial se establece como supersincrónica y, al impulsarla continuamente en la dirección de la velocidad en el apogeo, la órbita de transferencia se transforma en una órbita geosincrónica circular. Sin embargo, este método tarda mucho más en lograrse debido al bajo empuje inyectado en la órbita. ^[15]

Red de transporte interplanetario

En 1997 se publicó un conjunto de órbitas conocido como Red de Transporte Interplanetario (ITN), que proporciona trayectorias de delta- v propulsivo incluso más bajas (aunque mucho más lentas y largas) entre diferentes órbitas que las órbitas de transferencia de Hohmann. ^[16] La Red de Transporte Interplanetario es de naturaleza diferente a las transferencias de Hohmann porque las transferencias de Hohmann suponen un solo cuerpo grande, mientras que la Red de Transporte Interplanetario no. La Red de Transporte Interplanetario puede lograr el uso de delta- v propulsivo menor empleando la asistencia gravitatoria de los planetas. ^{[ cita requerida ]}

Véase también

• Portal de vuelos espaciales

• Transferencia bielíptica
• Presupuesto del delta-v
• Órbita de transferencia geoestacionaria
• Órbita de halo
• Órbita de Lissajous
• Lista de órbitas
• Mecánica orbital

Citas

1. Walter Hohmann, La alcanzabilidad de los cuerpos celestes (Washington: NASA Technical Translation F-44, 1960) Internet Archive.
2. Williams, Matt (26 de diciembre de 2014). "Hacer que el viaje a Marte sea más barato y más fácil: el caso de la captura balística". Universe Today . Consultado el 29 de julio de 2019 .
3. Hadhazy, Adam. "Una nueva forma de llegar a Marte de forma segura, en cualquier momento y a bajo coste". Scientific American . Consultado el 29 de julio de 2019 .
4. "Introducción a Bereshit y su trayectoria hacia la Luna". Gereshes . 2019-04-08 . Consultado el 2019-07-29 .
5. Jonathan McDowell, "Kick In the Apogee: 40 years of upper stage applications for solid rocket motors, 1957-1997", 33.ª Conferencia de Propulsión Conjunta de la AIAA, 4 de julio de 1997. Resumen. Consultado el 18 de julio de 2017.
6. NASA, Fundamentos de los vuelos espaciales , Sección 1, Capítulo 4, "Trayectorias". Consultado el 26 de julio de 2017. También disponible en spaceodyssey.dmns.org Archivado el 28 de julio de 2017 en Wayback Machine .
7. Tyson Sparks, Trajectories to Mars Archivado el 28 de octubre de 2017 en Wayback Machine , Colorado Center for Astrodynamics Research, 14/12/2012. Consultado el 25 de julio de 2017.
8. Langevin, Y. (2005). "Cuestiones de diseño para misiones científicas espaciales", Payload and Mission Definition in Space Sciences , V. Martínez Pillet, A. Aparicio y F. Sánchez, eds., Cambridge University Press, p. 30. ISBN 052185802X , 9780521858021 
9. Calla, Pablo; Fries, Dan; Welch, Chris (2018). "Minería de asteroides con naves espaciales pequeñas y su viabilidad económica". arXiv : 1808.05099 [astro-ph.IM].
10. Vallado, David Anthony (2001). Fundamentos de astrodinámica y aplicaciones. Springer. pág. 317. ISBN 0-7923-6903-3.
11. Curtis, Howard (2005). Mecánica orbital para estudiantes de ingeniería. Elsevier . p. 264. ISBN 0-7506-6169-0.
12. Vallado, David Anthony (2001). Fundamentos de astrodinámica y aplicaciones. Springer. pág. 318. ISBN 0-7923-6903-3.
13. Sternfeld, Ary J. (12 de febrero de 1934), "Sur les trajectoires permettant d'approcher d'un corpsattractif central à partir d'une orbite keplérienne donnée" [Sobre las trayectorias permitidas para acercarse a un cuerpo atractivo central desde un dada la órbita kepleriana], Comptes rendus de l'Académie des sciences (en francés), 198 (1), París: 711–713.
14. MIT, 16.522: Space Propulsion , Sesión 6, "Aproximaciones analíticas para maniobras de bajo empuje", primavera de 2015 (consultado el 26 de julio de 2017)
15. Spitzer, Arnon (1997). Trayectoria de órbita de transferencia óptima utilizando propulsión eléctrica. USPTO .
16. Lo, MW ; Ross, SD (1997). "Navegando por el Sistema Solar: Variedades Invariantes y la Dinámica del Sistema Solar". Informe Técnico . IOM. JPL . págs. 2–4. 312/97.

Fuentes generales y citadas

• Bate, RR; Mueller, DD; White, JE (1971). Fundamentos de la astrodinámica . Nueva York: Dover Publications. ISBN 978-0-486-60061-1.
• Battin, R. H. (1999). Introducción a las matemáticas y métodos de la astrodinámica . Washington, DC: Instituto Americano de Aeronáutica y Astronáutica. ISBN 978-1-56347-342-5.
• Hohmann, Walter (1925). Die Erreichbarkeit der Himmelskörper . Múnich: R. Oldenbourg Verlag. ISBN 3-486-23106-5.
• Thornton, Stephen T.; Marion, Jerry B. (2003). Dinámica clásica de partículas y sistemas (5.ª ed.). Brooks Cole . ISBN 0-534-40896-6.
• Vallado, DA (2001). Fundamentos de astrodinámica y aplicaciones (2ª ed.). Springer. ISBN 978-0-7923-6903-5.

Lectura adicional

• "Mecánica orbital". Tecnología espacial y de cohetes . Robert A. Braeunig. Archivado desde el original el 4 de febrero de 2012. Consultado el 17 de agosto de 2005 .
• "4. Trayectorias interplanetarias". Fundamentos de los vuelos espaciales . JPL: NASA .