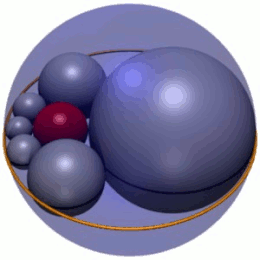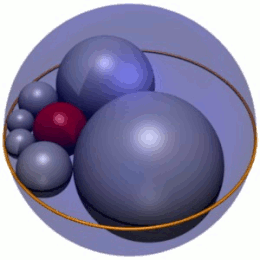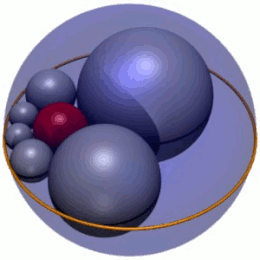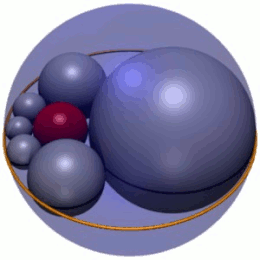
En geometría , el hexlet de Soddy es una cadena de seis esferas (mostradas en gris en la Figura 1), cada una de las cuales es tangente a sus dos vecinas y también a tres esferas dadas mutuamente tangentes. En la Figura 1, las tres esferas son la esfera interior roja y dos esferas (no mostradas) encima y debajo del plano en el que se encuentran los centros de las esferas hexlet. Además, las esferas hexlet son tangentes a una cuarta esfera (la esfera exterior azul en la Figura 1), que no es tangente a las otras tres.
Según un teorema publicado por Frederick Soddy en 1937, [ 1] siempre es posible encontrar un hexlet para cualquier elección de esferas mutuamente tangentes A , B y C. De hecho, existe una familia infinita de hexlets relacionados por la rotación y el escalamiento de las esferas de los hexlets (Figura 1); en esto, el hexlet de Soddy es el análogo esférico de una cadena de Steiner de seis círculos. [2] De acuerdo con las cadenas de Steiner, los centros de las esferas hexlet se encuentran en un solo plano, en una elipse. El maleficio de Soddy también se descubrió de forma independiente en Japón, como lo demuestran las tablillas Sangaku de 1822 en la prefectura de Kanagawa. [3]
El hexlet de Soddy es una cadena de seis esferas, denominadas S 1 – S 6 , cada una de las cuales es tangente a tres esferas dadas, A , B y C , que a su vez son mutuamente tangentes en tres puntos distintos. (Para mantener la coherencia a lo largo del artículo, las esferas hexlet siempre se representarán en gris, las esferas A y B en verde y la esfera C en azul). Las esferas hexlet también son tangentes a una cuarta esfera fija D (siempre mostrada en rojo) que no es tangente a los otros tres, A , B y C.
Cada esfera del hexlet de Soddy también es tangente a sus vecinas en la cadena; por ejemplo, la esfera S 4 es tangente a S 3 y S 5 . La cadena es cerrada, lo que significa que cada esfera de la cadena tiene dos vecinos tangentes; en particular, las esferas inicial y final, S 1 y S 6 , son tangentes entre sí.

El hexlet anular de Soddy es un caso especial (Figura 2), en el que las tres esferas mutuamente tangentes consisten en una sola esfera de radio r (azul) intercalada entre dos planos paralelos (verde) separados por una distancia perpendicular 2 r . En este caso, el hexlet de Soddy consta de seis esferas de radio r empaquetadas como rodamientos de bolas alrededor de la esfera central y también intercaladas. Las esferas hexlet también son tangentes a una cuarta esfera (roja), que no es tangente a las otras tres.
La cadena de seis esferas se puede girar alrededor de la esfera central sin afectar sus tangencias, lo que demuestra que existe una familia infinita de soluciones para este caso. A medida que se giran, las esferas del hexlet trazan un toro (una superficie en forma de rosquilla); en otras palabras, un toroide es la envoltura de esta familia de hexlets.
El problema general de encontrar un hexlet para tres esferas dadas A , B y C mutuamente tangentes se puede reducir al caso anular mediante inversión . Esta operación geométrica transforma siempre las esferas en esferas o en planos, que pueden considerarse esferas de radio infinito. Una esfera se transforma en un plano si y sólo si pasa por el centro de inversión. Una ventaja de la inversión es que conserva la tangencia; Si dos esferas son tangentes antes de la transformación, lo seguirán siendo después. Por lo tanto, si la transformación de inversión se elige juiciosamente, el problema se puede reducir a un caso más simple, como el hexlet anular de Soddy. La inversión es reversible; repetir una inversión en el mismo punto devuelve los objetos transformados a su tamaño y posición originales.
La inversión en el punto de tangencia entre las esferas A y B las transforma en planos paralelos, que pueden denotarse como a y b . Como la esfera C es tangente tanto a A como a B y no pasa por el centro de inversión, C se transforma en otra esfera c que es tangente a ambos planos; por lo tanto, c está intercalado entre los dos planos a y b . Este es el hexlet anular de Soddy (Figura 2). Se pueden empaquetar seis esferas s 1 – s 6 alrededor de c y también intercalarlas entre los planos delimitadores a y b . La reinversión restaura las tres esferas originales y transforma s 1 – s 6 en un hexlet para el problema original. En general, estas esferas hexlet S 1 – S 6 tienen radios diferentes.
Se puede generar una variedad infinita de hexlets girando las seis bolas s 1 – s 6 en su plano en un ángulo arbitrario antes de volver a invertirlas. La envoltura producida por tales rotaciones es el toro que rodea la esfera c y está intercalado entre los dos planos a y b ; por tanto, el toro tiene un radio interior r y un radio exterior 3 r . Después de la reinversión, este toro se convierte en un cíclido de Dupin (Figura 3).

La envoltura de los hexlets de Soddy es un cíclido de Dupin , una inversión del toroide . Así, la construcción de Soddy muestra que un cíclido de Dupin es la envoltura de una familia de esferas de 1 parámetro de dos maneras diferentes, y cada esfera de cualquier familia es tangente a dos esferas de la misma familia y tres esferas de la otra familia. [4] Este resultado probablemente era conocido por Charles Dupin , quien descubrió los cíclidos que llevan su nombre en su disertación de 1803 bajo la dirección de Gaspard Monge . [5]
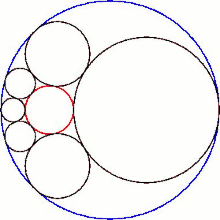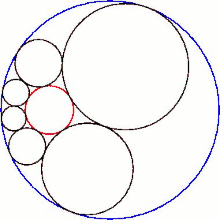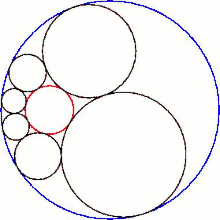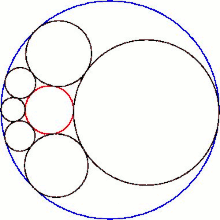
La intersección del hexlet con el plano de sus centros esféricos produce una cadena de Steiner de seis círculos.
Se supone que las esferas A y B tienen el mismo tamaño.
En cualquier hexlet elíptico , como el que se muestra en la parte superior del artículo, hay dos planos tangentes al hexlet. Para que exista un hexlet elíptico, el radio de C debe ser menor que un cuarto del de A. Si el radio de C es un cuarto del de A , cada esfera se convertirá en un plano en el viaje. Sin embargo, la imagen invertida muestra un hexlet elíptico normal, y en el hexlet parabólico , el punto donde una esfera se convierte en un plano es precisamente cuando su imagen invertida pasa por el centro de inversión. En tal hexlet sólo hay un plano tangente al hexlet. La línea de los centros de un hexlet parabólico es una parábola.
Si C es incluso mayor que eso, se forma un hexlet hiperbólico y ahora no hay ningún plano tangente. Etiqueta las esferas S 1 a S 6 . Por lo tanto, S 1 no puede ir muy lejos hasta que se convierte en un plano (donde su imagen invertida pasa por el centro de inversión) y luego invierte su concavidad (donde su imagen invertida rodea el centro de inversión). Ahora la recta de los centros es una hipérbola.
El caso límite es cuando A , B y C son todos del mismo tamaño. El hexlet ahora se vuelve recto. S 1 es pequeño cuando pasa por el agujero entre A , B y C , y crece hasta convertirse en un plano tangente a ellos. El centro de inversión ahora también está con un punto de tangencia con la imagen de S 6 , por lo que también es un plano tangente a A , B y C . A medida que S 1 avanza, su concavidad se invierte y ahora rodea todas las demás esferas, tangentes a A , B , C , S 2 y S 6 . S 2 empuja hacia arriba y crece hasta convertirse en un plano tangente y S 6 se contrae. S 1 obtiene entonces la posición anterior de S 6 como plano tangente. Luego invierte la concavidad nuevamente y pasa nuevamente por el agujero, comenzando otro viaje de ida y vuelta. Ahora bien, la línea de centros es una hipérbola degenerada , donde se ha colapsado en dos líneas rectas. [2]


Los matemáticos japoneses descubrieron el mismo hexlet más de cien años antes que Soddy. Analizaron los problemas de empaquetamiento en los que círculos y polígonos, bolas y poliedros entran en contacto y, a menudo, encontraron los teoremas relevantes de forma independiente antes de que los descubrieran los matemáticos occidentales. A menudo los publicaban como sangaku . El sangaku sobre el hexlet fue elaborado por Irisawa Shintarō Hiroatsu en la escuela de Uchida Itsumi y dedicado al Santuario Samukawa en mayo de 1822. El sangaku original se ha perdido, pero se registró en el libro Kokonsankan de Uchida en 1832. Una réplica del sangaku se hizo a partir del disco y se dedicó al museo Hōtoku en el Santuario Samukawa en agosto de 2009. [6]
El sangaku de Irisawa consta de tres problemas. El tercer problema se relaciona con el hexlet de Soddy: "el diámetro de la esfera circunscrita exterior es de 30 soles . Los diámetros de las bolas del núcleo son de 10 soles y 6 soles cada una. El diámetro de una de las bolas en la cadena de bolas es de 5 soles. Luego pregunté por los diámetros de las bolas restantes. La respuesta es 15 sol, 10 sol, 3,75 sol, 2,5 sol y 2 + 8/11 sol. [7]
En su respuesta, se escribe el método para calcular los diámetros de las bolas y, cuando se convierte a notación matemática occidental, se obtiene la siguiente solución. Si las relaciones entre el diámetro de la bola exterior y cada una de las bolas del núcleo son a 1 , a 2 , y si las relaciones entre el diámetro y las bolas de la cadena son c 1 , ..., c 6 . queremos representar c 2 , ..., c 6 en términos de a 1 , a 2 y c 1 . Si
entonces,
Entonces c 1 + c 4 = c 2 + c 5 = c 3 + c 6 .
Si r 1 , ..., r 6 son los diámetros de seis bolas, obtenemos la fórmula: