Gráfica (matemática discreta)

Un gráfico con seis vértices y siete aristas.

En matemáticas discretas , particularmente en teoría de grafos , un grafo es una estructura que consiste en un conjunto de objetos donde algunos pares de objetos están en algún sentido "relacionados". Los objetos están representados por abstracciones llamadas vértices (también llamados nodos o puntos ) y cada uno de los pares de vértices relacionados se llama arista (también llamado enlace o línea ). ^[1] Normalmente, un grafo se representa en forma diagramática como un conjunto de puntos o círculos para los vértices, unidos por líneas o curvas para las aristas.

Las aristas pueden ser dirigidas o no dirigidas. Por ejemplo, si los vértices representan a personas en una fiesta y hay una arista entre dos personas si se dan la mano, entonces este grafo no es dirigido porque cualquier persona A puede estrecharle la mano a una persona B solo si B también le estrecha la mano a A. Por el contrario, si una arista de una persona A a una persona B significa que A le debe dinero a B , entonces este grafo es dirigido, porque deber dinero no es necesariamente recíproco.

Los grafos son el objeto de estudio básico de la teoría de grafos. La palabra "grafo" fue utilizada por primera vez en este sentido por JJ Sylvester en 1878 debido a la relación directa entre las matemáticas y la estructura química (lo que él llamó una imagen químico-gráfica). ^[2]^[3]

Definiciones

Las definiciones en teoría de grafos varían. A continuación se presentan algunas de las formas más básicas de definir grafos y estructuras matemáticas relacionadas .

Gráfico

Un grafo (a veces llamado grafo no dirigido para distinguirlo de un grafo dirigido, o grafo simple para distinguirlo de un multigrafo ) ^[4]^[5] es un par $G = (V, E)$ , donde $V$ es un conjunto cuyos elementos se llaman vértices (singular: vértice), y $E$ es un conjunto de pares de vértices no ordenados, cuyos elementos se llaman aristas (a veces enlaces o líneas ). $\{v_{1},v_{2}\}$

Los vértices $u$ y $v$ de una arista ${u, v}$ se denominan extremos de la arista . Se dice que la arista une $u$ y $v$ e incide sobre ellos. Un vértice puede no pertenecer a ninguna arista, en cuyo caso no está unido a ningún otro vértice y se denomina aislado . Cuando existe una arista , los vértices $u$ y $v$ se denominan adyacentes . $\{u,v\}$

Un multigrafo es una generalización que permite que múltiples aristas tengan el mismo par de puntos finales. En algunos textos, los multigrafos se denominan simplemente grafos. ^[6]^[7]

A veces, se permite que los grafos contengan bucles , que son aristas que unen un vértice consigo mismo. Para permitir bucles, se debe permitir que los pares de vértices en $E$ tengan el mismo nodo dos veces. Estos grafos generalizados se denominan grafos con bucles o simplemente grafos cuando el contexto deja claro que se permiten los bucles.

En general, se considera que el conjunto de vértices $V$ es finito (lo que implica que el conjunto de aristas $E$ también es finito). A veces se consideran grafos infinitos , pero normalmente se los considera como un tipo especial de relación binaria , porque la mayoría de los resultados sobre grafos finitos no se extienden al caso infinito o necesitan una prueba bastante diferente.

Un grafo vacío es un grafo que tiene un conjunto vacío de vértices (y por lo tanto un conjunto vacío de aristas). El orden de un grafo es su número $| V |$ de vértices, normalmente denotado por $n$ . El tamaño de un grafo es su número $| E |$ de aristas, normalmente denotado por $m$ . Sin embargo, en algunos contextos, como para expresar la complejidad computacional de los algoritmos, el término tamaño se utiliza para la cantidad $| V | + | E |$ (de lo contrario, un grafo no vacío podría tener tamaño 0). El grado o valencia de un vértice es el número de aristas que le inciden; para grafos con bucles, un bucle se cuenta dos veces.

En un gráfico de orden $n$ , el grado máximo de cada vértice es $n - 1$ (o $n + 1$ si se permiten bucles, porque un bucle contribuye con 2 al grado), y el número máximo de aristas es $n (n - 1)/2$ (o $n (n + 1)/2$ si se permiten bucles).

Las aristas de un grafo definen una relación simétrica en los vértices, llamada relación de adyacencia . Específicamente, dos vértices $x$ e $y$ son adyacentes si ${x, y}$ es una arista. Un grafo está completamente determinado por su matriz de adyacencia $A$ , que es una matriz cuadrada $n \times n$ $, donde A ij$ especifica el número de conexiones del vértice $i$ al vértice $j$ . Para un grafo simple, $A ij$ es 0, lo que indica desconexión, o 1, lo que indica conexión; además $A ii = 0$ porque una arista en un grafo simple no puede comenzar y terminar en el mismo vértice. Los grafos con bucles propios se caracterizarán por que algunos o todos $los A ii$ sean iguales a un entero positivo, y los multigrafos (con múltiples aristas entre vértices) se caracterizarán por que algunos o todos $los A ij$ sean iguales a un entero positivo. Los grafos no dirigidos tendrán una matriz de adyacencia simétrica (lo que significa que $A ij = A ji$ ).

Grafo dirigido

Un gráfico dirigido con tres vértices y cuatro aristas dirigidas (la flecha doble representa una arista en cada dirección)

Un gráfico dirigido o dígrafo es un gráfico en el que los bordes tienen orientaciones.

En un sentido restringido pero muy común del término, ^[8] un gráfico dirigido es un par $G = (V, E)$ que comprende:

$V$ , un conjunto de vértices (también llamados nodos o puntos );
$E$ , un conjunto de aristas (también llamadas aristas dirigidas , enlaces dirigidos , líneas dirigidas , flechas o arcos ), que son pares ordenados de vértices distintos: . $E\subseteq \{(x,y)\mid (x,y)\in V^{2}\;{\textrm {and}}\;x\neq y\}$

Para evitar ambigüedades, este tipo de objeto puede llamarse precisamente un gráfico simple dirigido .

En la arista $(x, y)$ dirigida de $x$ a $y$ , los vértices $x$ e $y$ se denominan puntos finales de la arista, $x$ la cola de la arista e $y$ la cabeza de la arista. Se dice que la arista une $x$ e $y$ y que es incidente en $x$ y en $y$ . Un vértice puede existir en un grafo y no pertenecer a una arista. La arista $(y, x)$ se denomina arista invertida de $(x, y)$ . Las aristas múltiples , no permitidas según la definición anterior, son dos o más aristas con la misma cola y la misma cabeza.

En un sentido más general del término que permite múltiples aristas, ^[8] un gráfico dirigido a veces se define como un triple ordenado $G = (V, E, ϕ)$ que comprende:

$V$ , un conjunto de vértices (también llamados nodos o puntos );
$E$ , un conjunto de aristas (también llamadas aristas dirigidas , enlaces dirigidos , líneas dirigidas , flechas o arcos );
$ϕ$ , una función de incidencia que asigna cada arista a un par ordenado de vértices (es decir, una arista está asociada con dos vértices distintos): . $\phi :E\to \{(x,y)\mid (x,y)\in V^{2}\;{\textrm {and}}\;x\neq y\}$

Para evitar ambigüedades, este tipo de objeto puede llamarse precisamente un multigrafo dirigido .

Un bucle es una arista que une un vértice consigo mismo. Los grafos dirigidos, tal como se definen en las dos definiciones anteriores, no pueden tener bucles, porque un bucle que une un vértice consigo mismo es la arista (para un grafo simple dirigido) o es incidente en (para un multigrafo dirigido) que no está en . Por lo tanto, para permitir bucles, las definiciones deben expandirse. Para grafos simples dirigidos, la definición de debe modificarse a . Para multigrafos dirigidos, la definición de debe modificarse a . Para evitar ambigüedades, estos tipos de objetos pueden llamarse precisamente un grafo simple dirigido que permite bucles y un multigrafo dirigido que permite bucles (o un quiver ) respectivamente. $x$ $(x,x)$ $\{(x,y)\mid (x,y)\in V^{2}\;{\textrm {and}}\;x\neq y\}$ $E$ $E\subseteq \{(x,y)\mid (x,y)\in V^{2}\}$ $\phi$ $\phi :E\to \{(x,y)\mid (x,y)\in V^{2}\}$

Las aristas de un grafo simple dirigido que permite bucles $G$ es una relación homogénea ~ en los vértices de $G$ que se llama relación de adyacencia de $G$ . Específicamente, para cada arista $(x, y)$ , se dice que sus puntos finales $x$ e $y$ son adyacentes entre sí, lo que se denota $x ~ y$ .

Gráfico mixto

Un grafo mixto es un grafo en el que algunas aristas pueden ser dirigidas y otras no. Es un triple ordenado $G = (V, E, A)$ para un grafo simple mixto y $G = (V, E, A, ϕ E, ϕ A)$ para un multigrafo mixto con $V$ , $E$ (las aristas no dirigidas), $A$ (las aristas dirigidas), $ϕ E$ y $ϕ A$ definidas como se indicó anteriormente. Los grafos dirigidos y no dirigidos son casos especiales.

Gráfico ponderado

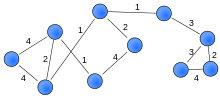
Un gráfico ponderado o una red ^[9]^[10] es un gráfico en el que se asigna un número (el peso) a cada arista. ^[11] Dichos pesos pueden representar, por ejemplo, costos, longitudes o capacidades, según el problema en cuestión. Dichos gráficos surgen en muchos contextos, por ejemplo, en problemas de ruta más corta, como el problema del viajante de comercio .

Tipos de gráficos

Gráfico orientado

Una definición de un grafo orientado es que es un grafo dirigido en el que como máximo uno de ( x , y ) y ( y , x ) pueden ser aristas del grafo. Es decir, es un grafo dirigido que se puede formar como una orientación de un grafo no dirigido (simple).

Algunos autores utilizan el término "grafo orientado" para referirse a lo mismo que "grafo dirigido". Algunos autores utilizan el término "grafo orientado" para referirse a cualquier orientación de un grafo no dirigido o multigrafo determinado.

Gráfico regular

Un grafo regular es un grafo en el que cada vértice tiene el mismo número de vecinos, es decir, cada vértice tiene el mismo grado. Un grafo regular con vértices de grado k se denomina grafo k -regular o grafo regular de grado k .

Gráfica completa

Un grafo completo es un grafo en el que cada par de vértices está unido por una arista. Un grafo completo contiene todas las aristas posibles.

Gráfico finito

Un grafo finito es un grafo en el que el conjunto de vértices y el conjunto de aristas son conjuntos finitos . De lo contrario, se denomina grafo infinito .

En teoría de grafos, lo más común es que se dé por sentado que los grafos analizados son finitos. Si los grafos son infinitos, esto suele indicarse específicamente.

Grafo conectado

En un grafo no dirigido, un par de vértices no ordenados { x , y } se denomina conexo si un camino conduce de x a y . De lo contrario, el par no ordenado se denomina desconectado .

Un grafo conexo es un grafo no dirigido en el que cada par de vértices no ordenados del grafo está conexo. De lo contrario, se denomina grafo desconectado .

En un grafo dirigido, un par ordenado de vértices ( x , y ) se denomina fuertemente conectado si un camino dirigido conduce de x a y . De lo contrario, el par ordenado se denomina débilmente conectado si un camino no dirigido conduce de x a y después de reemplazar todas sus aristas dirigidas por aristas no dirigidas. De lo contrario, el par ordenado se denomina desconectado .

Un grafo fuertemente conexo es un grafo dirigido en el que cada par ordenado de vértices en el grafo está fuertemente conexo. De lo contrario, se denomina grafo débilmente conexo si cada par ordenado de vértices en el grafo está débilmente conexo. De lo contrario, se denomina grafo desconectado .

Un grafo conexo por k vértices o conexo por k aristas es un grafo en el que no existe ningún conjunto de k − 1 vértices (respectivamente, aristas) que, al eliminarse, desconecte el grafo. Un grafo conexo por k vértices suele denominarse simplemente grafo conexo por k .

Gráfico bipartito

Un grafo bipartito es un grafo simple en el que el conjunto de vértices se puede dividir en dos conjuntos, W y X , de modo que ningún par de vértices en W comparta una arista común y ningún par de vértices en X comparta una arista común. Alternativamente, es un grafo con un número cromático de 2.

En un gráfico bipartito completo , el conjunto de vértices es la unión de dos conjuntos disjuntos, W y X , de modo que cada vértice en W es adyacente a cada vértice en X pero no hay aristas dentro de W o X.

Gráfico de ruta

Un grafo de trayectoria o grafo lineal de orden n ≥ 2 es un grafo en el que los vértices se pueden enumerar en un orden v ₁ , v ₂ , …, v _n tal que las aristas son { v _i , v _{i +1} } donde i = 1, 2, …, n − 1. Los grafos de trayectoria se pueden caracterizar como grafos conexos en los que el grado de todos los vértices menos dos es 2 y el grado de los dos vértices restantes es 1. Si un grafo de trayectoria ocurre como un subgrafo de otro grafo, es una trayectoria en ese grafo.

Gráfico planar

Un gráfico plano es un gráfico cuyos vértices y aristas se pueden dibujar en un plano de manera que ninguna de las aristas se cruce.

Gráfica de ciclo

Un grafo de ciclo o grafo circular de orden n ≥ 3 es un grafo en el que los vértices se pueden enumerar en un orden v ₁ , v ₂ , …, v _n tal que las aristas son { v _i , v _{i +1} } donde i = 1, 2, …, n − 1, más la arista { v _n , v ₁ } . Los grafos de ciclo se pueden caracterizar como grafos conexos en los que el grado de todos los vértices es 2. Si un grafo de ciclo ocurre como un subgrafo de otro grafo, es un ciclo o circuito en ese grafo.

Árbol

Un árbol es un gráfico no dirigido en el que dos vértices están conectados exactamente por un camino , o equivalentemente, un gráfico no dirigido acíclico conectado .

Un bosque es un gráfico no dirigido en el que dos vértices están conectados como máximo por un camino, o equivalentemente un gráfico no dirigido acíclico, o equivalentemente una unión disjunta de árboles.

Poliárbol

Un poliárbol (o árbol dirigido o árbol orientado o red simplemente conectada ) es un gráfico acíclico dirigido (DAG) cuyo gráfico no dirigido subyacente es un árbol.

Un polibosque (o bosque dirigido o bosque orientado ) es un gráfico acíclico dirigido cuyo gráfico no dirigido subyacente es un bosque.

Clases avanzadas

Los tipos de gráficos más avanzados son:

Gráfico de Petersen y sus generalizaciones;
gráficos perfectos ;
cografías ;
grafos cordales ;
otros gráficos con grandes grupos de automorfismos : gráficos transitivos de vértice , transitivos de arco y transitivos de distancia ;
grafos fuertemente regulares y sus generalizaciones grafos distancia-regulares .

Propiedades de los gráficos

Dos aristas de un grafo se denominan adyacentes si comparten un vértice común. Dos aristas de un grafo dirigido se denominan consecutivas si la cabeza de la primera es la cola de la segunda. De manera similar, dos vértices se denominan adyacentes si comparten una arista común ( consecutivas si la primera es la cola y la segunda es la cabeza de una arista), en cuyo caso se dice que la arista común une los dos vértices. Una arista y un vértice sobre esa arista se denominan incidentes .

El grafo con un solo vértice y sin aristas se denomina grafo trivial . Un grafo con solo vértices y sin aristas se conoce como grafo sin aristas . El grafo sin vértices ni aristas a veces se denomina grafo nulo o grafo vacío , pero la terminología no es uniforme y no todos los matemáticos admiten este objeto.

Normalmente, los vértices de un grafo, por su naturaleza como elementos de un conjunto, son distinguibles. Este tipo de grafo puede llamarse vértice-labeled . Sin embargo, para muchas preguntas es mejor tratar los vértices como indistinguibles. (Por supuesto, los vértices pueden ser distinguibles por las propiedades del propio grafo, por ejemplo, por el número de aristas incidentes). Las mismas observaciones se aplican a las aristas, por lo que los grafos con aristas etiquetadas se denominan edge-labeled . Los grafos con etiquetas adjuntas a las aristas o vértices se designan más generalmente como labeled . En consecuencia, los grafos en los que los vértices son indistinguibles y las aristas son indistinguibles se denominan unlabeled . (En la literatura, el término labeled puede aplicarse a otros tipos de etiquetado, además de aquel que sirve solo para distinguir diferentes vértices o aristas).

La categoría de todos los gráficos es la categoría de coma Conjunto ↓ D donde D : Conjunto → Conjunto es el funtor que toma un conjunto s en s × s .

Ejemplos

El diagrama es una representación esquemática del gráfico con vértices y aristas. $V=\{1,2,3,4,5,6\}$ $E=\{\{1,2\},\{1,5\},\{2,3\},\{2,5\},\{3,4\},\{4,5\},\{4,6\}\}.$
En informática , los gráficos dirigidos se utilizan para representar conocimiento (por ejemplo, gráficos conceptuales ), máquinas de estados finitos y muchas otras estructuras discretas.
Una relación binaria R sobre un conjunto X define un grafo dirigido. Un elemento x de X es predecesor directo de un elemento y de X si y solo si xRy .
Un gráfico dirigido puede modelar redes de información como Twitter , donde un usuario sigue a otro. ^[12]^[13]
Ejemplos particularmente regulares de grafos dirigidos son los grafos de Cayley de grupos finitamente generados, así como los grafos de coconjuntos de Schreier.
En la teoría de categorías , cada categoría pequeña tiene un multigrafo dirigido subyacente cuyos vértices son los objetos de la categoría y cuyos bordes son las flechas de la categoría. En el lenguaje de la teoría de categorías, se dice que hay un funtor olvidadizo desde la categoría de categorías pequeñas hasta la categoría de carcaj .

Operaciones gráficas

Existen varias operaciones que producen nuevos gráficos a partir de los iniciales, que podrían clasificarse en las siguientes categorías:

operaciones unarias , que crean un nuevo gráfico a partir de uno inicial, como por ejemplo:
- contracción del borde ,
- gráfico lineal ,
- gráfico dual
- gráfico complementario ,
- reescritura de gráficos ;
operaciones binarias , que crean un nuevo grafo a partir de dos iniciales, como por ejemplo:

Generalizaciones

En un hipergrafo , una arista puede unir cualquier número positivo de vértices.

Un grafo no dirigido puede verse como un complejo simplicial que consta de 1- símplices (las aristas) y 0-símplices (los vértices). Como tales, los complejos son generalizaciones de grafos, ya que permiten la existencia de símplices de dimensiones superiores.

Cada gráfico da lugar a un matroide .

En la teoría de modelos , un grafo es simplemente una estructura . Pero en ese caso, no hay límite en cuanto al número de aristas: puede ser cualquier número cardinal , véase grafo continuo .

En biología computacional , el análisis de gráficos de potencia introduce los gráficos de potencia como una representación alternativa de gráficos no dirigidos.

En los sistemas de información geográfica , las redes geométricas se modelan de cerca a partir de gráficos y toman prestados muchos conceptos de la teoría de grafos para realizar análisis espaciales en redes de carreteras o redes de servicios públicos.

Véase también

Notas

^ Trudeau, Richard J. (1993). Introducción a la teoría de grafos (edición corregida y ampliada). Nueva York: Dover Pub. p. 19. ISBN 978-0-486-67870-2. Archivado desde el original el 5 de mayo de 2019 . Consultado el 8 de agosto de 2012 . Un grafo es un objeto que consta de dos conjuntos llamados su conjunto de vértices y su conjunto de aristas .
^
Ver:
- JJ Sylvester (7 de febrero de 1878) "Química y álgebra", Archivado el 4 de febrero de 2023 en Wayback Machine. Nature , 17 : 284. doi :10.1038/017284a0. De la página 284: "Todo invariante y covariante se vuelve así expresable mediante un gráfico exactamente idéntico a un diagrama o quimicograma de Kekulé".
- JJ Sylvester (1878) "Sobre una aplicación de la nueva teoría atómica a la representación gráfica de los invariantes y covariantes de la cuántica binaria, con tres apéndices", Archivado el 4 de febrero de 2023 en Wayback Machine. American Journal of Mathematics, Pure and Applied , 1 (1): 64–90. doi :10.2307/2369436. JSTOR 2369436. El término "grafo" aparece por primera vez en este artículo en la página 65.
^ Gross, Jonathan L.; Yellen, Jay (2004). Manual de teoría de grafos. CRC Press . p. 35. ISBN. 978-1-58488-090-5Archivado desde el original el 4 de febrero de 2023. Consultado el 16 de febrero de 2016 .
^ Bender y Williamson 2010, pág. 148.
^ Véase, por ejemplo, Iyanaga y Kawada, 69 J , p. 234 o Biggs, pág. 4.
^ Bender y Williamson 2010, pág. 149.
^ Graham y otros, pág. 5.
^ desde Bender y Williamson 2010, pág. 161.
^ Strang, Gilbert (2005), Álgebra lineal y sus aplicaciones (4.ª ed.), Brooks Cole, ISBN 978-0-03-010567-8
^ Lewis, John (2013), Estructuras de software Java (4.ª ed.), Pearson, pág. 405, ISBN 978-0133250121
^ Fletcher, Peter; Hoyle, Hughes; Patty, C. Wayne (1991). Fundamentos de las matemáticas discretas (edición internacional para estudiantes). Boston: PWS-KENT Pub. Co. p. 463. ISBN 978-0-53492-373-0Un gráfico ponderado es un gráfico en el que se asigna un número w ( e ) , llamado su peso , a cada arista e .
^ Grandjean, Martin (2016). «Un análisis de la red social de Twitter: mapeo de la comunidad de humanidades digitales». Cogent Arts & Humanities . 3 (1): 1171458. doi : 10.1080/23311983.2016.1171458 . Archivado desde el original el 2021-03-02 . Consultado el 2019-09-16 .
^ Pankaj Gupta, Ashish Goel, Jimmy Lin, Aneesh Sharma, Dong Wang y Reza Bosagh Zadeh WTF: El sistema de a quién seguir en Twitter Archivado el 12 de julio de 2019 en Wayback Machine , Actas de la 22.ª conferencia internacional sobre la World Wide Web . doi :10.1145/2488388.2488433.

Referencias

Balakrishnan, VK (1997). Teoría de grafos (1.ª ed.). McGraw-Hill. ISBN 978-0-07-005489-9.
Bang-Jensen, J.; Gutin, G. (2000). Dígrafos: teoría, algoritmos y aplicaciones. Springer.
Bender, Edward A.; Williamson, S. Gill (2010). Listas, decisiones y gráficos. Con una introducción a la probabilidad.
Bergé, Claude (1958). Théorie des graphes et ses aplicaciones (en francés). París: Dunod.
Biggs, Norman (1993). Teoría de grafos algebraicos (2.ª ed.). Cambridge University Press. ISBN 978-0-521-45897-9.
Bollobás, Béla (2002). Teoría de grafos moderna (1ª ed.). Saltador. ISBN 978-0-387-98488-9.
Diestel, Reinhard (2005). Teoría de grafos (3ª ed.). Berlín, Nueva York: Springer-Verlag. ISBN 978-3-540-26183-4.
Graham, RL; Grötschel, M.; Lovász, L. (1995). Manual de combinatoria . Prensa del MIT. ISBN 978-0-262-07169-7.
Gross, Jonathan L.; Yellen, Jay (1998). Teoría de grafos y sus aplicaciones . CRC Press. ISBN 978-0-8493-3982-0.
Gross, Jonathan L.; Yellen, Jay (2003). Manual de teoría de grafos . CRC. ISBN 978-1-58488-090-5.
Harary, Frank (1995). Teoría de grafos . Addison Wesley Publishing Company. ISBN 978-0-201-41033-4.
Iyanaga, Shôkichi; Kawada, Yukiyosi (1977). Diccionario enciclopédico de matemáticas . Prensa del MIT. ISBN 978-0-262-09016-2.
Zwillinger, Daniel (2002). Tablas y fórmulas matemáticas estándar del CRC (31.ª edición). Chapman & Hall/CRC. ISBN 978-1-58488-291-6.

Lectura adicional

Trudeau, Richard J. (1993). Introducción a la teoría de grafos (edición corregida y ampliada). Nueva York: Dover Publications . ISBN 978-0-486-67870-2. Recuperado el 8 de agosto de 2012 .

Enlaces externos

Recursos de la biblioteca sobre
gráficos (matemáticas)

Recursos en tu biblioteca

Medios relacionados con Grafo (matemáticas discretas) en Wikimedia Commons
Weisstein, Eric W. "Gráfico". MathWorld .