Cómo comprobar si una moneda es justa

En estadística , la cuestión de comprobar si una moneda es justa es una cuestión cuya importancia radica, en primer lugar, en proporcionar un problema simple con el que ilustrar las ideas básicas de la inferencia estadística y, en segundo lugar, en proporcionar un problema simple que se puede utilizar para comparar varios métodos de inferencia estadística en competencia, incluida la teoría de la decisión . El problema práctico de comprobar si una moneda es justa podría considerarse como algo que se resuelve fácilmente realizando un número suficientemente grande de ensayos, pero la estadística y la teoría de la probabilidad pueden proporcionar orientación sobre dos tipos de cuestiones; específicamente, las de cuántos ensayos realizar y la de la precisión de una estimación de la probabilidad de que salga cara, derivada de una muestra dada de ensayos.

Una moneda justa es un dispositivo de aleatorización idealizado con dos estados (generalmente llamados "cara" y "cruz" ) que tienen la misma probabilidad de ocurrir. Se basa en el lanzamiento de moneda que se usa ampliamente en deportes y otras situaciones en las que se requiere dar a dos partes la misma probabilidad de ganar. Se usa una ficha especialmente diseñada o, más habitualmente, una moneda simple , aunque esta última puede ser ligeramente "injusta" debido a una distribución asimétrica del peso, que puede hacer que un estado ocurra con más frecuencia que el otro, dando a una de las partes una ventaja injusta. ^[1] Por lo tanto, puede ser necesario probar experimentalmente si la moneda es de hecho "justa", es decir, si la probabilidad de que la moneda caiga de cualquier lado cuando se lanza es exactamente del 50%. Por supuesto, es imposible descartar desviaciones arbitrariamente pequeñas de la imparcialidad, como podría esperarse que afecten solo a un lanzamiento en una vida de lanzamientos; también es siempre posible que una moneda injusta (o " sesgada ") salga exactamente 10 caras en 20 lanzamientos. Por lo tanto, cualquier prueba de imparcialidad debe establecer únicamente un cierto grado de confianza en un cierto grado de imparcialidad (un cierto sesgo máximo). En una terminología más rigurosa, el problema es determinar los parámetros de un proceso de Bernoulli , dada únicamente una muestra limitada de ensayos de Bernoulli .

Preámbulo

En este artículo se describen los procedimientos experimentales para determinar si una moneda es justa o no. Existen muchos métodos estadísticos para analizar un procedimiento experimental de este tipo. En este artículo se ilustran dos de ellos.

Ambos métodos establecen un experimento (o prueba) en el que se lanza la moneda muchas veces y se registra el resultado de cada lanzamiento. Los resultados pueden luego analizarse estadísticamente para decidir si la moneda es "justa" o "probablemente no justa".

• Función de densidad de probabilidad posterior o PDF ( enfoque bayesiano ). Inicialmente, se desconoce la probabilidad real de obtener un lado particular cuando se lanza una moneda, pero la incertidumbre está representada por la " distribución previa ". La teoría de la inferencia bayesiana se utiliza para derivar la distribución posterior combinando la distribución previa y la función de verosimilitud que representa la información obtenida del experimento. La probabilidad de que esta moneda en particular sea una "moneda justa" se puede obtener integrando la PDF de la distribución posterior sobre el intervalo relevante que representa todas las probabilidades que se pueden considerar "justas" en un sentido práctico.
• Estimador de probabilidad verdadera ( enfoque frecuentista ). Este método supone que el experimentador puede decidir lanzar la moneda cualquier número de veces. El experimentador decide primero el nivel de confianza requerido y el margen de error tolerable. Estos parámetros determinan el número mínimo de lanzamientos que se deben realizar para completar el experimento.

Una diferencia importante entre estos dos enfoques es que el primero da cierto peso a la experiencia previa de lanzamiento de monedas, mientras que el segundo no. La cuestión de cuánto peso se debe dar a la experiencia previa, dependiendo de la calidad (credibilidad) de esa experiencia, se analiza en la teoría de la credibilidad .

Función de densidad de probabilidad posterior

Un método es calcular la función de densidad de probabilidad posterior de la teoría de probabilidad bayesiana .

Se realiza una prueba lanzando la moneda N veces y anotando el número observado de caras, h , y cruces, t . Los símbolos H y T representan variables más generalizadas que expresan el número de caras y cruces, respectivamente, que podrían haberse observado en el experimento. Por lo tanto, N = H + T = h + t .

A continuación, supongamos que r es la probabilidad real de obtener cara en un solo lanzamiento de la moneda. Esta es la propiedad de la moneda que se está investigando. Utilizando el teorema de Bayes , la densidad de probabilidad posterior de r condicional a h y t se expresa de la siguiente manera:

${\displaystyle f(r\mid H=h,T=t)={\frac {\Pr(H=h\mid r,N=h+t)\,g(r)}{\int _{0}^{1}\Pr(H=h\mid p,N=h+t)\,g(p)\,dp}},}$

donde g ( r ) representa la distribución de densidad de probabilidad previa de r , que se encuentra en el rango de 0 a 1.

La distribución de densidad de probabilidad previa resume lo que se sabe sobre la distribución de r en ausencia de cualquier observación. Supondremos que la distribución previa de r es uniforme en el intervalo [0, 1]. Es decir, g ( r ) = 1. (En la práctica, sería más apropiado suponer una distribución previa que tenga una ponderación mucho mayor en la región de alrededor de 0,5, para reflejar nuestra experiencia con monedas reales).

La probabilidad de obtener h caras en N lanzamientos de una moneda con una probabilidad de cara igual a r viene dada por la distribución binomial :

${\displaystyle \Pr(H=h\mid r,N=h+t)={N \choose h}r^{h}(1-r)^{t}.}$

Sustituyendo esto en la fórmula anterior:

${\displaystyle f(r\mid H=h,T=t)={\frac {{N \choose h}r^{h}(1-r)^{t}}{\int _{0}^{1}{N \choose h}p^{h}(1-p)^{t}\,dp}}={\frac {r^{h}(1-r)^{t}}{\int _{0}^{1}p^{h}(1-p)^{t}\,dp}}.}$

Se trata, de hecho, de una distribución beta (la conjugada anterior de la distribución binomial), cuyo denominador puede expresarse en términos de la función beta :

${\displaystyle f(r\mid H=h,T=t)={\frac {1}{\mathrm {B} (h+1,t+1)}}r^{h}(1-r)^{t}.}$

Como se ha asumido una distribución previa uniforme, y debido a que h y t son números enteros, esto también se puede escribir en términos de factoriales :

${\displaystyle f(r\mid H=h,T=t)={\frac {(h+t+1)!}{h!\,t!}}r^{h}(1-r)^{t}.}$

Ejemplo

Por ejemplo, sea N = 10, h = 7, es decir, se lanza la moneda 10 veces y se obtienen 7 caras:

${\displaystyle f(r\mid H=7,T=3)={\frac {(10+1)!}{7!\,3!}}r^{7}(1-r)^{3}=1320\,r^{7}(1-r)^{3}.}$

El gráfico de la derecha muestra la función de densidad de probabilidad de r dado que se obtuvieron 7 caras en 10 lanzamientos. (Nota: r es la probabilidad de obtener cara al lanzar la misma moneda una vez).

Gráfico de la densidad de probabilidad f ( r  |  H  = 7,  T  = 3) = 1320  r ⁷  (1 −  r ) ³ con r entre 0 y 1

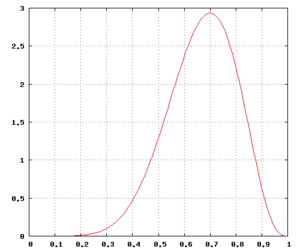
La probabilidad de una moneda imparcial (definida para este propósito como una cuya probabilidad de caer cara está entre el 45% y el 55%)

${\displaystyle \Pr(0.45<r<0.55)=\int _{0.45}^{0.55}f(p\mid H=7,T=3)\,dp\approx 13\%\!}$

es pequeña en comparación con la hipótesis alternativa (una moneda sesgada). Sin embargo, no es lo suficientemente pequeña como para hacernos creer que la moneda tiene un sesgo significativo. Esta probabilidad es ligeramente superior a nuestra presuposición de la probabilidad de que la moneda fuera justa correspondiente a la distribución previa uniforme, que era del 10%. Utilizando una distribución previa que refleje nuestro conocimiento previo de lo que es una moneda y cómo actúa, la distribución posterior no favorecería la hipótesis del sesgo. Sin embargo, el número de ensayos en este ejemplo (10 lanzamientos) es muy pequeño, y con más ensayos la elección de la distribución previa sería algo menos relevante.)

Con la distribución de probabilidad a posteriori uniforme, la distribución de probabilidad a posteriori f ( r  |  H  = 7, T  = 3) alcanza su pico en r  =  h  / ( h  +  t ) = 0,7; este valor se denomina estimación máxima a posteriori (MAP) de r . Además, con la distribución a posteriori uniforme, el valor esperado de r bajo la distribución a posteriori es

${\displaystyle \operatorname {E} [r]=\int _{0}^{1}r\cdot f(r\mid H=7,T=3)\,\mathrm {d} r={\frac {h+1}{h+t+2}}={\frac {2}{3}}.}$

Estimador de probabilidad verdadera

Utilizando este enfoque, para decidir el número de veces que se debe lanzar la moneda, se requieren dos parámetros:

1. El nivel de confianza que se denota por el intervalo de confianza (Z)
2. El error máximo (aceptable) (E)

• El nivel de confianza se denota por Z y se da por el valor Z de una distribución normal estándar . Este valor se puede leer en una tabla de estadísticas de puntuación estándar para la distribución normal. Algunos ejemplos son:

• El error máximo (E) se define por donde es la probabilidad estimada de obtener cara. Nota: es la misma probabilidad real (de obtener cara) que en la sección anterior de este artículo. ${\displaystyle |p-r|<E}$ ${\displaystyle p\,\!}$ ${\displaystyle r}$ ${\displaystyle r\,\!}$
• En estadística, la estimación de una proporción de una muestra (denotada por p ) tiene un error estándar dado por:

${\displaystyle s_{p}={\sqrt {\frac {p\,(1-p)}{n}}}}$

donde n es el número de ensayos (que fue denotado por N en la sección anterior).

Esta función de error estándar de p tiene un máximo en . Además, en el caso de lanzar una moneda, es probable que p no esté lejos de 0,5, por lo que es razonable suponer que p = 0,5 en los siguientes casos: ${\displaystyle s_{p}}$ ${\displaystyle p=(1-p)=0.5}$

Y por lo tanto el valor del error máximo (E) viene dado por

Resolviendo el número requerido de lanzamientos de moneda, n ,

${\displaystyle n={\frac {Z^{2}}{4\,E^{2}}}\!}$

Ejemplos

1. Si se desea un error máximo de 0,01, ¿cuántas veces se debe lanzar la moneda?

${\displaystyle n={\frac {Z^{2}}{4\,E^{2}}}={\frac {Z^{2}}{4\times 0.01^{2}}}=2500\ Z^{2}}$

${\displaystyle n=2500\,}$con un nivel de confianza del 68,27% (Z=1)

${\displaystyle n=10000\,}$con un nivel de confianza del 95,45% (Z=2)

${\displaystyle n=27225\,}$con un nivel de confianza del 99,90% (Z=3,3)

2. Si se lanza la moneda 10000 veces, ¿cuál es el error máximo del estimador sobre el valor de (la probabilidad real de obtener cara en un lanzamiento de moneda)? ${\displaystyle p\,\!}$ ${\displaystyle r\,\!}$

${\displaystyle E={\frac {Z}{2\,{\sqrt {n}}}}}$

${\displaystyle E={\frac {Z}{2\,{\sqrt {10000}}}}={\frac {Z}{200}}}$

${\displaystyle E=0.0050\,}$con un nivel de confianza del 68,27% (Z=1)

${\displaystyle E=0.0100\,}$con un nivel de confianza del 95,45% (Z=2)

${\displaystyle E=0.0165\,}$con un nivel de confianza del 99,90% (Z=3,3)

3. Se lanza la moneda 12000 veces y el resultado es 5961 caras (y 6039 cruces). ¿ En qué intervalo se encuentra el valor de (la probabilidad real de obtener cara) si se desea un nivel de confianza del 99,999 %? ${\displaystyle r\,\!}$

${\displaystyle p={\frac {h}{h+t}}\,={\frac {5961}{12000}}\,=0.4968}$

Ahora encuentre el valor de Z correspondiente al nivel de confianza del 99,999%.

${\displaystyle Z=4.4172\,\!}$

Ahora calcula E

${\displaystyle E={\frac {Z}{2\,{\sqrt {n}}}}\,={\frac {4.4172}{2\,{\sqrt {12000}}}}\,=0.0202}$

El intervalo que contiene r es entonces:

${\displaystyle p-E<r<p+E\,\!}$

${\displaystyle 0.4766<r<0.5170\,\!}$

Otros enfoques

Existen otros enfoques para la cuestión de comprobar si una moneda es justa, que utilizan la teoría de la decisión , cuya aplicación requeriría la formulación de una función de pérdida o una función de utilidad que describa las consecuencias de tomar una decisión determinada. Un enfoque que evita requerir una función de pérdida o una probabilidad previa (como en el enfoque bayesiano) es el del "muestreo de aceptación". ^[2]

Otras aplicaciones

El análisis matemático anterior para determinar si una moneda es justa también se puede aplicar a otros usos. Por ejemplo:

• Determinación de la proporción de elementos defectuosos de un producto sometido a una condición particular (pero bien definida). A veces, un producto puede ser muy difícil o costoso de producir. Además, si la prueba de dichos productos dará como resultado su destrucción, se debe probar un número mínimo de elementos. Mediante un análisis similar, se puede encontrar la función de densidad de probabilidad de la tasa de defectos del producto.
• Sondeo entre dos partidos. Si se realiza una encuesta con una muestra aleatoria pequeña en la que sólo hay dos opciones mutuamente excluyentes, esto es similar a lanzar una misma moneda varias veces utilizando una moneda posiblemente sesgada. Por lo tanto, se puede aplicar un análisis similar para determinar la confianza que se debe atribuir a la proporción real de votos emitidos. (Si a las personas se les permite abstenerse , el análisis debe tenerlo en cuenta, y la analogía del lanzamiento de una moneda no es del todo válida).
• Determinación de la proporción de sexos en un grupo grande de una especie animal. Siempre que se tome una muestra aleatoria pequeña (es decir, pequeña en comparación con la población total) al realizar el muestreo aleatorio de la población, el análisis es similar a la determinación de la probabilidad de obtener cara en el lanzamiento de una moneda.

Véase también

• Prueba binomial
• Lanzamiento de moneda
• Intervalo de confianza
• Teoría de la estimación
• Estadística inferencial
• Dados cargados
• Margen de error
• Estimación puntual
• Aleatoriedad estadística

Referencias

1. Sin embargo, si la moneda se atrapa en lugar de dejarla rebotar o girar, es difícil sesgar el resultado de un lanzamiento de moneda. Véase Gelman , Andrew; Deborah Nolan (2002). "El rincón del profesor: se puede cargar un dado, pero no se puede sesgar una moneda". American Statistician . 56 (4): 308–311. doi :10.1198/000313002605. S2CID  123597087.
2. Cox, DR, Hinkley, DV (1974) Estadística teórica (Ejemplo 11.7), Chapman & Hall. ISBN 0-412-12420-3 

• Guttman, Wilks y Hunter: Introducción a la estadística en ingeniería , John Wiley & Sons, Inc. (1971) ISBN 0-471-33770-6 
• Devinder Sivia: Análisis de datos, un tutorial bayesiano , Oxford University Press (1996) ISBN 0-19-851889-7