Bitangentes de un cuarto grado

28 líneas que tocan una curva plana cuártica general en dos lugares

La curva de Trott y siete de sus bitangentes. Las demás son simétricas respecto de rotaciones de 90° a través del origen.

La curva de Trott con las 28 bitangentes.

En la teoría de curvas planas algebraicas , una curva plana cuártica general tiene 28 líneas bitangentes , líneas que son tangentes a la curva en dos lugares. Estas líneas existen en el plano proyectivo complejo , pero es posible definir curvas cuárticas para las cuales todas estas 28 líneas tienen números reales como coordenadas y, por lo tanto, pertenecen al plano euclidiano .

Una cuártica explícita con veintiocho bitangentes reales fue dada por primera vez por Plücker  (1839) ^[1] Como mostró Plücker, el número de bitangentes reales de cualquier cuártica debe ser 28, 16 o un número menor que 9. Otra cuártica con 28 bitangentes reales puede formarse mediante el lugar geométrico de los centros de elipses con longitudes de eje fijas, tangentes a dos líneas no paralelas. ^[2] Shioda (1995) dio una construcción diferente de una cuártica con veintiocho bitangentes, formada mediante la proyección de una superficie cúbica ; veintisiete de las bitangentes de la curva de Shioda son reales, mientras que la vigésimo octava es la línea en el infinito en el plano proyectivo.

Ejemplo

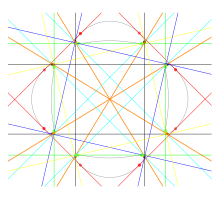
La curva de Trott , otra curva con 28 bitangentes reales, es el conjunto de puntos ( x , y ) que satisfacen la ecuación polinomial de grado cuatro

${\displaystyle \displaystyle 144(x^{4}+y^{4})-225(x^{2}+y^{2})+350x^{2}y^{2}+81=0.}$

Estos puntos forman una curva cuártica no singular que tiene género tres y que tiene veintiocho bitangentes reales . ^[3]

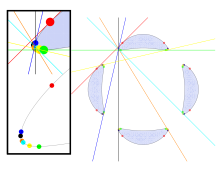
Al igual que los ejemplos de Plücker y de Blum y Guinand, la curva de Trott tiene cuatro óvalos separados, el número máximo para una curva de grado cuatro, y por lo tanto es una curva M. Los cuatro óvalos se pueden agrupar en seis pares diferentes de óvalos; para cada par de óvalos hay cuatro bitangentes que tocan ambos óvalos del par, dos que separan los dos óvalos y dos que no. Además, cada óvalo limita una región no convexa del plano y tiene una bitangente que abarca la porción no convexa de su límite.

Conexiones con otras estructuras

La curva dual de una curva cuártica tiene 28 puntos dobles ordinarios reales, duales a las 28 bitangentes de la curva primal.

Las 28 bitangentes de un cuártico también pueden colocarse en correspondencia con símbolos de la forma

${\displaystyle {\begin{bmatrix}a&b&c\\d&e&f\\\end{bmatrix}}}$

donde a, b, c, d, e, f son todos cero o uno y donde

${\displaystyle ad+be+cf=1\ (\operatorname {mod} \ 2).}$^[4]

Hay 64 opciones para a, b, c, d, e, f , pero solo 28 de ellas producen una suma impar. También se pueden interpretar a, b, c como las coordenadas homogéneas de un punto del plano de Fano y d, e, f como las coordenadas de una línea en el mismo plano proyectivo finito; la condición de que la suma sea impar es equivalente a exigir que el punto y la línea no se toquen, y hay 28 pares diferentes de un punto y una línea que no se tocan.

Los puntos y líneas del plano de Fano que están disjuntos de un par punto-línea no incidente forman un triángulo, y las bitangentes de un cuártico se han considerado como en correspondencia con los 28 triángulos del plano de Fano. ^[5] El gráfico de Levi del plano de Fano es el gráfico de Heawood , en el que los triángulos del plano de Fano están representados por 6-ciclos. Los 28 6-ciclos del gráfico de Heawood a su vez corresponden a los 28 vértices del gráfico de Coxeter . ^[6]

Las 28 bitangentes de un cuártico también corresponden a pares de las 56 líneas en una superficie del Pezzo de grado 2 , ^[5] y a las 28 características theta impares .

Las 27 líneas de la cúbica y las 28 bitangentes de una cuártica, junto con los 120 planos tritangentes de una curva séxtica canónica de género 4, forman una " trinidad " en el sentido de Vladimir Arnold , específicamente una forma de correspondencia de McKay , ^{[7] [8] [9]} y pueden relacionarse con muchos otros objetos, incluidos E ₇ y E ₈ , como se analiza en trinidades .

Notas

1. Véase, por ejemplo, Gray (1982).
2. Blum y Guinand (1964).
3. Trott (1997).
4. Riemann (1876); Cayley (1879).
5. Manivel (2006).
6. Dejter, Italo J. (2011), "Del gráfico de Coxeter al gráfico de Klein", Journal of Graph Theory , 70 : 1–9, arXiv : 1002.1960 , doi : 10.1002/jgt.20597, S2CID  754481.
7. Le Bruyn, Lieven (17 de junio de 2008), Las trinidades de Arnold, archivado desde el original el 11 de abril de 2011
8. Arnold 1997, p. 13 – Arnold, Vladimir, 1997, Conferencias de Toronto, Conferencia 2: Simplificación, complejización y trinidades matemáticas, junio de 1997 (última actualización en agosto de 1998). TeX, PostScript, PDF
9. (McKay y Sebbar 2007, pág. 11)

Referencias

• Blum, R.; Guinand, AP (1964). "Una cuártica con 28 bitangentes reales". Canadian Mathematical Bulletin . 7 (3): 399–404. doi :10.4153/cmb-1964-038-6.
• Cayley, Arthur (1879), "Sobre las bitangentes de una cuártica", Salmon's Higher Plane Curves , págs. 387–389. En Los artículos matemáticos recopilados de Arthur Cayley , Andrew Russell Forsyth, ed., The University Press, 1896, vol. 11, págs. 221–223.
• Gray, Jeremy (1982), "De la historia de un grupo simple", The Mathematical Intelligencer , 4 (2): 59–67, CiteSeerX  10.1.1.163.2944 , doi :10.1007/BF03023483, MR  0672918, S2CID  14602496. Reimpreso en Levy, Silvio, ed. (1999), The Eightfold Way , MSRI Publications, vol. 35, Cambridge University Press, págs. 115-131, ISBN 0-521-66066-1, Sr.  1722415.
• Manivel, L. (2006), "Configuraciones de líneas y modelos de álgebras de Lie", Journal of Algebra , 304 (1): 457–486, arXiv : math/0507118 , doi : 10.1016/j.jalgebra.2006.04.029 , S2CID  17374533.
• McKay, John; Sebbar, Abdellah (2007). "Funciones replicables: una introducción". Fronteras en teoría de números, física y geometría II . págs. 373–386. doi :10.1007/978-3-540-30308-4_10. ISBN 978-3-540-30307-7.
• Plücker, J. (1839), Theorie der algebraischen Curven: gegrundet auf eine neue Behandlungsweise der analytischen Geometrie , Berlín: Adolph Marcus.
• Riemann, GFB (1876), "Zur Theorie der Abel'schen Funktionen für den Fall p  = 3", Ges. Werke , Leipzig, págs. 456–472{{citation}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace )Según lo citado por Cayley.
• Shioda, Tetsuji (1995), "Transformaciones de Weierstrass y superficies cúbicas" (PDF) , Commentarii Mathematici Universitatis Sancti Pauli , 44 (1): 109–128, MR  1336422
• Trott, Michael (1997), "Aplicación de la base de Groebner a tres problemas de geometría", Mathematica en educación e investigación , 6 (1): 15–28.