En matemáticas y álgebra computacional , la diferenciación automática ( autodiferenciación , autodiff o AD ), también llamada diferenciación algorítmica , diferenciación computacional , [1] [2] es un conjunto de técnicas para evaluar la derivada parcial de una función especificada por un programa de computadora.
La diferenciación automática aprovecha el hecho de que cada cálculo informático, por complicado que sea, ejecuta una secuencia de operaciones aritméticas elementales (suma, resta, multiplicación, división, etc.) y funciones elementales ( exp , log , sen , cos , etc.). Al aplicar la regla de la cadena repetidamente a estas operaciones, se pueden calcular derivadas parciales de orden arbitrario de forma automática, con precisión de trabajo y utilizando como máximo un pequeño factor constante de más operaciones aritméticas que el programa original.

La diferenciación automática es distinta de la diferenciación simbólica y la diferenciación numérica . La diferenciación simbólica enfrenta la dificultad de convertir un programa de computadora en una sola expresión matemática y puede conducir a un código ineficiente. La diferenciación numérica (el método de diferencias finitas) puede introducir errores de redondeo en el proceso de discretización y cancelación. Ambos métodos clásicos tienen problemas con el cálculo de derivadas superiores, donde la complejidad y los errores aumentan. Finalmente, ambos métodos clásicos son lentos al calcular derivadas parciales de una función con respecto a muchas entradas, como es necesario para los algoritmos de optimización basados en gradientes . La diferenciación automática resuelve todos estos problemas.
La diferenciación automática es particularmente importante en el campo del aprendizaje automático . Por ejemplo, permite implementar la retropropagación en una red neuronal sin una derivada calculada manualmente.
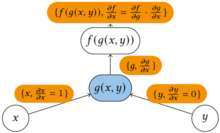
Fundamental para la diferenciación automática es la descomposición de las diferenciales proporcionada por la regla de la cadena de derivadas parciales de funciones compuestas . Para la composición simple, la regla de la cadena da
Generalmente se presentan dos modos distintos de diferenciación automática.
La acumulación hacia adelante especifica que uno recorre la regla de la cadena desde adentro hacia afuera (es decir, primero computar y luego y por último ), mientras que la acumulación inversa tiene el recorrido desde afuera hacia adentro (primero computar y luego y por último ). Más sucintamente,
El valor de la derivada parcial, llamada semilla , se propaga hacia adelante o hacia atrás y es inicialmente o . La acumulación hacia adelante evalúa la función y calcula la derivada con respecto a una variable independiente en una pasada. Por lo tanto, para cada variable independiente es necesario un paso separado en el que la derivada con respecto a esa variable independiente se establece en uno ( ) y la de todas las demás en cero ( ). Por el contrario, la acumulación inversa requiere las funciones parciales evaluadas para las derivadas parciales. Por lo tanto, la acumulación inversa evalúa primero la función y calcula las derivadas con respecto a todas las variables independientes en un paso adicional.
Cuál de estos dos tipos se debe utilizar depende del número de barridos. La complejidad computacional de un barrido es proporcional a la complejidad del código original.
La retropropagación de errores en perceptrones multicapa, una técnica utilizada en el aprendizaje automático , es un caso especial de acumulación inversa. [2]
La acumulación hacia adelante fue introducida por RE Wengert en 1964. [3] Según Andreas Griewank, la acumulación inversa se ha sugerido desde finales de la década de 1960, pero se desconoce quién la inventó. [4] Seppo Linnainmaa publicó la acumulación inversa en 1976. [5]
En la AD de acumulación hacia adelante, primero se fija la variable independiente con respecto a la cual se realiza la diferenciación y se calcula la derivada de cada subexpresión de manera recursiva. En un cálculo con lápiz y papel, esto implica sustituir repetidamente la derivada de las funciones internas en la regla de la cadena: Esto se puede generalizar a múltiples variables como un producto matricial de jacobianos .
En comparación con la acumulación inversa, la acumulación hacia adelante es natural y fácil de implementar, ya que el flujo de información de las derivadas coincide con el orden de evaluación. Cada variable se complementa con su derivada (almacenada como un valor numérico, no como una expresión simbólica), como se indica con el punto. Las derivadas se calculan luego en sincronía con los pasos de evaluación y se combinan con otras derivadas mediante la regla de la cadena.
Usando la regla de la cadena, si tiene predecesores en el gráfico computacional:

A modo de ejemplo, considere la función: Para mayor claridad, las subexpresiones individuales se han etiquetado con las variables .
La elección de la variable independiente a la que se realiza la diferenciación afecta los valores semilla ẇ 1 y ẇ 2 . Dado el interés en la derivada de esta función con respecto a x 1 , los valores semilla deben establecerse en:
Una vez establecidos los valores iniciales, los valores se propagan utilizando la regla de la cadena, como se muestra. La figura 2 muestra una representación gráfica de este proceso como un gráfico computacional.
Para calcular el gradiente de esta función de ejemplo, que requiere no solo sino también , se realiza un barrido adicional sobre el gráfico computacional utilizando los valores semilla .
La acumulación hacia adelante calcula la función y la derivada (pero solo para una variable independiente cada una) en una sola pasada. La llamada al método asociado espera que la expresión Z se derive con respecto a una variable V. El método devuelve un par de la función evaluada y su derivada. El método recorre el árbol de expresiones recursivamente hasta que se alcanza una variable. Si se solicita la derivada con respecto a esta variable, su derivada es 1, 0 en caso contrario. Luego se evalúan la función parcial así como la derivada parcial. [6]
tupla < float , float > evaluarYDerivar ( Expresión Z , Variable V ) { if isVariable ( Z ) if ( Z = V ) return { valueOf ( Z ), 1 }; else return { valueOf ( Z ), 0 }; else if ( Z = A + B ) { a , a ' } = evaluarYDerivar ( A , V ); { b , b ' } = evaluarYDerivar ( B , V ); return { a + b , a ' + b ' }; else if ( Z = A - B ) { a , a ' } = evaluarYDerivar ( A , V ); { b , b ' } = evaluarYDerivar ( B , V ); return { a - b , a ' - b ' }; else if ( Z = A * B ) { a , a ' } = evaluarYDerivar ( A , V ); { b , b ' } = evaluarYDeriva ( B , V ); devolver { a * b , b * a ' + a * b ' }; } #include <iostream> struct ValueAndPartial { float valor , parcial ; }; struct Variable ; struct Expresión { virtual ValueAndPartial evaluarAndDerive ( Variable * variable ) = 0 ; }; struct Variable : pública Expresión { float valor ; Variable ( float valor ) : valor ( valor ) {} ValueAndPartial evaluarAndDerive ( Variable * variable ) { float parcial = ( this == variable ) ? 1.0f : 0.0f ; return { valor , parcial }; } }; struct Plus : pública Expresión { Expresión * a , * b ; Plus ( Expresión * a , Expresión * b ) : a ( a ), b ( b ) {} ValueAndPartial evaluarAndDerive ( Variable * variable ) { auto [ valorA , parcialA ] = a -> evaluarAndDerive ( variable ); auto [ valorB , parcialB ] = b -> evaluarYDeriva ( variable ); return { valorA + valorB , parcialA + parcialB }; } }; struct Multiplicar : public Expresión { Expresión * a , * b ; Multiplicar ( Expresión * a , Expresión * b ) : a ( a ), b ( b ) {} ValorYPartial evaluarYDeriva ( Variable * variable ) { auto [ valorA , parcialA ] = a -> evaluarYDeriva ( variable ); auto [ valorB , parcialB ] = b -> evaluarYDeriva ( variable ); return { valorA * valorB , valorB * parcialA + valorA * parcialB }; } }; int main () { // Ejemplo: Encontrar los parciales de z = x * (x + y) + y * y en (x, y) = (2, 3) Variable x ( 2 ), y ( 3 ); Más p1 ( & x , & y ) ; Multiplica m1 ( & x , & p1 ); Multiplica m2 ( & y , & y ) ; Más z ( & m1 , & m2 ); float xPartial = z .evaluarYDeriva ( & x ) .parcial ; float yPartial = z .evaluarAndDerive ( & y ) .parcial ; std :: cout << "∂z/∂x = " << xPartial << ", " << "∂z/∂y = " << yPartial << std:: endl ; // Salida : ∂z / ∂x = 7 , ∂z / ∂y = 8 return 0 ; } 
En la AD de acumulación inversa, la variable dependiente que se va a diferenciar es fija y la derivada se calcula con respecto a cada subexpresión de forma recursiva. En un cálculo con lápiz y papel, la derivada de las funciones externas se sustituye repetidamente en la regla de la cadena:
En la acumulación inversa, la cantidad de interés es el adjunto , denotado con una barra ; es una derivada de una variable dependiente elegida con respecto a una subexpresión :
Usando la regla de la cadena, si tiene sucesores en el gráfico computacional:
La acumulación inversa recorre la regla de la cadena desde el exterior hacia el interior o, en el caso del gráfico computacional de la Figura 3, desde arriba hacia abajo. La función de ejemplo tiene un valor escalar y, por lo tanto, solo hay una semilla para el cálculo de la derivada y solo se necesita un barrido del gráfico computacional para calcular el gradiente (de dos componentes). Esto es solo la mitad del trabajo en comparación con la acumulación hacia adelante, pero la acumulación inversa requiere el almacenamiento de las variables intermedias w i, así como las instrucciones que las produjeron en una estructura de datos conocida como "cinta" o lista de Wengert [7] (sin embargo, Wengert publicó la acumulación hacia adelante, no la acumulación inversa [3] ), que puede consumir una memoria significativa si el gráfico computacional es grande. Esto se puede mitigar hasta cierto punto almacenando solo un subconjunto de las variables intermedias y luego reconstruyendo las variables de trabajo necesarias repitiendo las evaluaciones, una técnica conocida como rematerialización . Los puntos de control también se utilizan para guardar estados intermedios.

Las operaciones para calcular la derivada mediante acumulación inversa se muestran en la siguiente tabla (observe el orden inverso):
El gráfico de flujo de datos de un cálculo se puede manipular para calcular el gradiente de su cálculo original. Esto se hace añadiendo un nodo adjunto para cada nodo primario, conectado por aristas adjuntas que son paralelas a las aristas primarias pero fluyen en la dirección opuesta. Los nodos en el gráfico adjunto representan la multiplicación por las derivadas de las funciones calculadas por los nodos en el primario. Por ejemplo, la adición en el primario causa un abanico de salida en el adjunto; el abanico de salida en el primario causa una adición en el adjunto; [a] una función unaria y = f ( x ) en el primario causa x̄ = ȳ f ′( x ) en el adjunto; etc.
La acumulación inversa requiere dos pasadas: en la pasada hacia adelante, primero se evalúa la función y se almacenan en caché los resultados parciales. En la pasada inversa, se calculan las derivadas parciales y se retropropaga el valor derivado previamente. La llamada al método correspondiente espera que se derive la expresión Z y se genere como semilla el valor derivado de la expresión principal. Para la expresión superior, Z derivada con respecto a Z, este es 1. El método recorre el árbol de expresiones de forma recursiva hasta que se alcanza una variable y agrega el valor semilla actual a la expresión derivada. [8] [9]
void derive ( Expresión Z , float semilla ) { if isVariable ( Z ) derivadaPartialDe ( Z ) += semilla ; else if ( Z = A + B ) derive ( A , semilla ); derive ( B , semilla ); else if ( Z = A - B ) derive ( A , semilla ); derive ( B , - semilla ); else if ( Z = A * B ) derive ( A , valorDe ( B ) * semilla ); derive ( B , valorDe ( A ) * semilla ); } #include <iostream> struct Expresión { float valor ; virtual void evaluar () = 0 ; virtual void derivar ( float semilla ) = 0 ; }; struct Variable : pública Expresión { float parcial ; Variable ( float valor ) { this -> valor = valor ; parcial = 0.0f ; } void evaluar () {} void derivar ( float semilla ) { parcial += semilla ; } }; struct Más : pública Expresión { Expresión * a , * b ; Más ( Expresión * a , Expresión * b ) : a ( a ), b ( b ) {} void evaluar () { a -> evaluar (); b -> evaluar (); valor = a -> valor + b -> valor ; } void derivar ( float semilla ) { a -> derivar ( semilla ); b -> derivar ( semilla ); } }; struct Multiplicar : pública Expresión { Expresión * a , * b ; Multiplicar ( Expresión * a , Expresión * b ) : a ( a ), b ( b ) {} void evaluar () { a -> evaluar (); b -> evaluar (); valor = a -> valor * b -> valor ; } void derive ( float seed ) { a -> derive ( b -> valor * semilla ); b -> derive ( a -> valor * semilla ); } }; int main () { // Ejemplo: Encontrar los parciales de z = x * (x + y) + y * y en (x, y) = (2, 3) Variable x ( 2 ), y ( 3 ); Más p1 ( & x , & y ); Multiplica m1 ( & x , & p1 ); Multiplica m2 ( & y , & y ); Más z ( & m1 , & m2 ); z . evaluar (); std :: cout << "z = " << z . valor << std :: endl ; // Salida: z = 19 z . derivar ( 1 ); std :: cout << "∂z/∂x = " << x . parcial << ", " << "∂z/∂y = " << y . parcial << std :: endl ; // Salida: ∂z/∂x = 7, ∂z/∂y = 8 return 0 ; } La acumulación hacia adelante y hacia atrás son sólo dos formas (extremas) de recorrer la regla de la cadena. El problema de calcular un jacobiano completo de f : R n → R m con un número mínimo de operaciones aritméticas se conoce como el problema de acumulación jacobiana óptima (OJA), que es NP-completo . [10] Central para esta prueba es la idea de que pueden existir dependencias algebraicas entre los parciales locales que etiquetan los bordes del grafo. En particular, dos o más etiquetas de borde pueden reconocerse como iguales. La complejidad del problema aún está abierta si se supone que todas las etiquetas de borde son únicas y algebraicamente independientes.
La diferenciación automática en modo directo se logra aumentando el álgebra de números reales y obteniendo una nueva aritmética . Se agrega un componente adicional a cada número para representar la derivada de una función en el número, y todos los operadores aritméticos se extienden para el álgebra aumentada. El álgebra aumentada es el álgebra de números duales .
Reemplace cada número con el número , donde es un número real, pero es un número abstracto con la propiedad (un infinitesimal ; consulte Análisis infinitesimal suavizado ). Usando solo esto, la aritmética regular da como resultado .
Ahora, los polinomios se pueden calcular en esta aritmética aumentada. Si , entonces donde denota la derivada de con respecto a su primer argumento, y , llamada semilla , se puede elegir arbitrariamente.
La nueva aritmética consta de pares ordenados , elementos escritos , con aritmética ordinaria en el primer componente y aritmética de diferenciación de primer orden en el segundo componente, como se describió anteriormente. Extender los resultados anteriores sobre polinomios a funciones analíticas da una lista de la aritmética básica y algunas funciones estándar para la nueva aritmética: y en general para la función primitiva , donde y son las derivadas de con respecto a sus primer y segundo argumentos, respectivamente.
Cuando se aplica una operación aritmética básica binaria a argumentos mixtos (el par y el número real ), el número real se eleva primero a . La derivada de una función en el punto se encuentra ahora calculando con la aritmética anterior, que da como resultado .
A continuación se muestra un ejemplo de implementación basado en el enfoque de número dual.
Doble más (Dual A, Dual B) { devolver { parterealDe(A) + parterealDe(B), parteinfinitaDe(A) + parteinfinitaDe(B) };}Doble menos (Dual A, Dual B) { devolver { parterealDe(A) - parterealDe(B), infinitesimalPartOf(A) - infinitesimalPartOf(B) };}Doble multiplicación (Dual A, Dual B) { devolver { parterealDe(A) * parterealDe(B), ParterealDe(B) * ParteinfinitsimalDe(A) + ParterealDe(A) * ParteinfinitsimalDe(B) };}X = {x, 0};Y = {y, 0};Épsilon = {0, 1};xPartial = infinitesimalPartOf(f(X + Epsilon, Y));yPartial = infinitesimalPartOf(f(X, Y + Epsilon));#include <iostream> struct Dual { float partereal , parteinfinitesimal ; Dual ( float partereal , float parteinfinitesimal = 0 ) : partereal ( partereal ), parteinfinitesimal ( parteinfinitesimal ) {} Operador dual + ( dual otro ) { return dual ( partereal + otro . partereal , parteinfinitesimal + otro . parteinfinitesimal ); } Operador dual * ( dual otro ) { return dual ( partereal * otro . partereal , otro . partereal * parteinfinitesimal + partereal * otro . parteinfinitesimal ); } }; // Ejemplo: Encontrar los parciales de z = x * (x + y) + y * y en (x, y) = (2, 3) Dual f ( dual x , dual y ) { return x * ( x + y ) + y * y ; } int main () { dual x = dual ( 2 ); dual y = dual ( 3 ); Epsilon dual = Dual ( 0 , 1 ); a dual = f ( x + epsilon , y ); b dual = f ( x , y + epsilon ); std :: cout << "∂z/∂x = " << a . infinitesimalPart << ", " << "∂z/∂y = " << b . infinitesimalPart << std :: endl ; // Salida: ∂z/∂x = 7, ∂z/∂y = 8 return 0 ; } Las funciones multivariadas se pueden manejar con la misma eficiencia y mecanismos que las funciones univariadas adoptando un operador de derivada direccional. Es decir, si es suficiente calcular , la derivada direccional de en la dirección se puede calcular como utilizando la misma aritmética que antes. Si se desean todos los elementos de , entonces se requieren evaluaciones de funciones. Nótese que en muchas aplicaciones de optimización, la derivada direccional es de hecho suficiente.
La aritmética anterior se puede generalizar para calcular derivadas de segundo orden y superiores de funciones multivariadas. Sin embargo, las reglas aritméticas se complican rápidamente: la complejidad es cuadrática en el grado de derivada más alto. En su lugar, se puede utilizar el álgebra polinómica de Taylor truncada . La aritmética resultante, definida en números duales generalizados, permite un cálculo eficiente utilizando funciones como si fueran un tipo de datos. Una vez que se conoce el polinomio de Taylor de una función, las derivadas se extraen fácilmente.
El AD en modo directo se implementa mediante una interpretación no estándar del programa en la que los números reales se reemplazan por números duales, las constantes se elevan a números duales con un coeficiente épsilon cero y las primitivas numéricas se elevan para operar en números duales. Esta interpretación no estándar generalmente se implementa utilizando una de dos estrategias: transformación del código fuente o sobrecarga de operadores .

El código fuente de una función se reemplaza por un código fuente generado automáticamente que incluye declaraciones para calcular las derivadas intercaladas con las instrucciones originales.
La transformación del código fuente se puede implementar para todos los lenguajes de programación y también es más fácil para el compilador realizar optimizaciones en tiempo de compilación. Sin embargo, la implementación de la herramienta AD en sí es más difícil y el sistema de compilación es más complejo.

La sobrecarga de operadores es una posibilidad para el código fuente escrito en un lenguaje que la admita. Los objetos para números reales y operaciones matemáticas elementales deben sobrecargarse para satisfacer la aritmética aumentada que se muestra arriba. Esto no requiere ningún cambio en la forma o secuencia de operaciones en el código fuente original para que la función se diferencie, pero a menudo requiere cambios en los tipos de datos básicos para números y vectores para admitir la sobrecarga y, a menudo, también implica la inserción de operaciones de señalización especiales. Debido a la sobrecarga inherente de la sobrecarga de operadores en cada bucle, este enfoque generalmente demuestra un rendimiento de velocidad más débil.
Los operadores sobrecargados se pueden utilizar para extraer el gráfico de valoración, seguido de la generación automática de la versión AD de la función primaria en tiempo de ejecución. A diferencia de la AAD OO clásica, dicha función AD no cambia de una iteración a la siguiente. Por lo tanto, no hay sobrecarga en tiempo de ejecución de interpretación OO o de cinta por cada muestra Xi.
Al generar la función AD en tiempo de ejecución, se puede optimizar para tener en cuenta el estado actual del programa y calcular previamente ciertos valores. Además, se puede generar de manera que utilice de manera consistente la vectorización de CPU nativa para procesar fragmentos de datos de usuario de 4(8) veces el doble (AVX2\AVX512 acelera x4-x8). Si se tiene en cuenta el subprocesamiento múltiple, este enfoque puede generar una aceleración final del orden de 8 × #Cores en comparación con las herramientas AAD tradicionales. Hay una implementación de referencia disponible en GitHub. [11]
{{cite book}}: CS1 maint: multiple names: authors list (link){{cite book}}: CS1 maint: multiple names: authors list (link){{cite journal}}: CS1 maint: multiple names: authors list (link)