Las aplicaciones biológicas de la teoría de la bifurcación proporcionan un marco para comprender el comportamiento de las redes biológicas modeladas como sistemas dinámicos . En el contexto de un sistema biológico, la teoría de la bifurcación describe cómo pequeños cambios en un parámetro de entrada pueden causar una bifurcación o un cambio cualitativo en el comportamiento del sistema. La capacidad de realizar cambios drásticos en la salida del sistema suele ser esencial para el funcionamiento del organismo y, por lo tanto, las bifurcaciones son omnipresentes en las redes biológicas, como los interruptores del ciclo celular .
Las redes biológicas se originan a partir de la evolución y, por lo tanto, tienen componentes menos estandarizados e interacciones potencialmente más complejas que las redes diseñadas por los humanos, como las redes eléctricas . A nivel celular, los componentes de una red pueden incluir una gran variedad de proteínas, muchas de las cuales difieren entre organismos. Las interacciones de red ocurren cuando una o más proteínas afectan la función de otra a través de la transcripción , traducción , translocación , fosforilación u otros mecanismos. Estas interacciones activan o inhiben la acción de la proteína objetivo de alguna manera. Si bien los humanos construyen redes con una preocupación por la simplicidad y el orden, las redes biológicas adquieren redundancia y complejidad a lo largo de la evolución. Por lo tanto, puede ser imposible predecir el comportamiento cuantitativo de una red biológica a partir del conocimiento de su organización. De manera similar, es imposible describir su organización puramente a partir de su comportamiento, aunque el comportamiento puede indicar la presencia de ciertos motivos de red .

Sin embargo, con el conocimiento de las interacciones de la red y un conjunto de parámetros para las proteínas y las interacciones de las proteínas (generalmente obtenidos a través de la investigación empírica ), a menudo es posible construir un modelo de la red como un sistema dinámico . En general, para n proteínas, el sistema dinámico toma la siguiente forma [1] donde x es típicamente la concentración de proteínas:
Estos sistemas suelen ser muy difíciles de resolver, por lo que es más fácil modelar las redes como sistemas dinámicos lineales . Los sistemas lineales no contienen productos entre x y siempre son solucionables. Tienen la siguiente forma para todos los i:
Desafortunadamente, los sistemas biológicos a menudo son no lineales y, por lo tanto, necesitan modelos no lineales.
A pesar de la gran complejidad y diversidad potencial de las redes biológicas, todo comportamiento de red de primer orden se generaliza a uno de cuatro posibles motivos de entrada-salida: hiperbólico o Michaelis-Menten , ultrasensible , biestable y biestable irreversible (una biestabilidad en la que se necesita una entrada negativa y, por lo tanto, biológicamente imposible para volver de un estado de alta salida). Se pueden encontrar ejemplos de cada uno en contextos biológicos en sus respectivas páginas.
Las redes ultrasensibles, biestables e irreversiblemente biestables muestran cambios cualitativos en el comportamiento de la red alrededor de ciertos valores de parámetros: estos son sus puntos de bifurcación.

Los sistemas dinámicos no lineales se pueden entender más fácilmente con un sistema de ejemplo unidimensional donde el cambio en la abundancia de alguna cantidad x (por ejemplo, concentración de proteínas) depende solo de sí mismo:
En lugar de resolver el sistema analíticamente, lo que puede resultar difícil o imposible para muchas funciones, suele ser más rápido y más informativo adoptar un enfoque geométrico y dibujar un retrato de fase . Un retrato de fase es un bosquejo cualitativo del comportamiento de la ecuación diferencial que muestra soluciones de equilibrio o puntos fijos y el campo vectorial en la línea real.
Las bifurcaciones describen cambios en la estabilidad o la existencia de puntos fijos a medida que cambia un parámetro de control en el sistema. Como explicación muy simple de una bifurcación en un sistema dinámico, considere un objeto equilibrado sobre una viga vertical. La masa del objeto puede considerarse como el parámetro de control, r , y la desviación de la viga con respecto al eje vertical es la variable dinámica , x . A medida que r aumenta, x permanece relativamente estable. Pero cuando la masa alcanza un cierto punto (el punto de bifurcación), la viga se doblará repentinamente, en una dirección que depende de pequeñas imperfecciones en la configuración. Este es un ejemplo de una bifurcación en horquilla. Los cambios en el parámetro de control eventualmente cambiaron el comportamiento cualitativo del sistema.
Para un ejemplo más riguroso, considere el sistema dinámico que se muestra en la Figura 2, descrito por la siguiente ecuación:
donde r es nuevamente el parámetro de control (etiquetado ε en la Figura 2). Los puntos fijos del sistema están representados por donde la curva de retrato de fase cruza el eje x. La estabilidad de un punto fijo dado se puede determinar por la dirección del flujo en el eje x; por ejemplo, en la Figura 2, el punto verde es inestable (flujo divergente) y el rojo es estable (flujo convergente). Al principio, cuando r es mayor que 0, el sistema tiene un punto fijo estable y un punto fijo inestable. A medida que r disminuye, los puntos fijos se mueven juntos, chocan brevemente en un punto fijo semiestable en r = 0 y luego dejan de existir cuando r < 0.
En este caso, debido a que el comportamiento del sistema cambia significativamente cuando el parámetro de control r es 0, 0 es un punto de bifurcación . Al rastrear la posición de los puntos fijos en la Figura 2 a medida que r varía, se puede generar el diagrama de bifurcación que se muestra en la Figura 3.
Otros tipos de bifurcaciones también son importantes en los sistemas dinámicos, pero la bifurcación en silla de montar tiende a ser la más importante en biología. Los sistemas biológicos reales están sujetos a pequeñas variaciones estocásticas que introducen términos de error en las ecuaciones dinámicas, y esto generalmente conduce a bifurcaciones más complejas que se simplifican en nodos de silla de montar separados y puntos fijos. Dos ejemplos de bifurcaciones "imperfectas" que pueden aparecer en biología se analizan a continuación. Obsérvese que el propio nodo de silla de montar en presencia de error simplemente se traslada en el plano xr , sin cambios en el comportamiento cualitativo; esto se puede demostrar utilizando el mismo análisis que se presenta a continuación.

Una bifurcación simple común es la bifurcación transcrítica , dada por
y el diagrama de bifurcación en la Figura 4 (curvas negras). Los diagramas de fase se muestran en la Figura 5. Siguiendo las intersecciones con el eje x en el diagrama de fase a medida que r cambia, hay dos trayectorias de puntos fijos que se intersecan en el origen; este es el punto de bifurcación (intuitivamente, cuando cambia el número de intersecciones con el eje x en el retrato de fase). El punto fijo izquierdo siempre es inestable y el derecho estable.

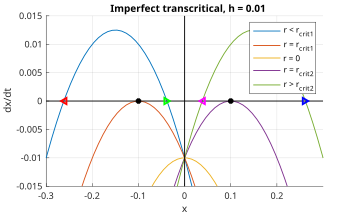
Consideremos ahora la adición de un término de error h , donde 0 < h << 1. Es decir,
El término de error traslada todos los retratos de fase verticalmente, hacia abajo si h es positivo. En la mitad izquierda de la Figura 6 ( x < 0), los puntos fijos negro, rojo y verde son semiestables, inestables y estables, respectivamente. Esto se refleja en los puntos magenta, negro y azul de la mitad derecha ( x > 0). Cada una de estas mitades se comporta así como una bifurcación de nodo-silla; en otras palabras, la bifurcación transcrítica imperfecta puede aproximarse mediante dos bifurcaciones de nodo-silla cuando están cerca de los puntos críticos, como es evidente en las curvas rojas de la Figura 4.
Además de observar el flujo en los diagramas de fases, también es posible demostrar la estabilidad de varios puntos fijos mediante el análisis de estabilidad lineal . En primer lugar, busque los puntos fijos en el diagrama de fases estableciendo la ecuación de bifurcación en 0:
Usando la fórmula cuadrática para encontrar los puntos fijos x* :
donde en el último paso se ha utilizado la aproximación 4 h << r 2 , lo cual es razonable para estudiar puntos fijos mucho más allá del punto de bifurcación, como las curvas azul claro y verde de la Figura 6. Simplificando aún más,
A continuación, determine si la curva de retrato de fase está aumentando o disminuyendo en los puntos fijos, lo que se puede evaluar introduciendo x * en la primera derivada de la ecuación de bifurcación.
Los resultados se complican por el hecho de que r puede ser tanto positivo como negativo; no obstante, las conclusiones son las mismas que antes en lo que respecta a la estabilidad de cada punto fijo. Esto no es ninguna sorpresa, ya que la primera derivada contiene la misma información que el análisis de flujo del diagrama de fases. Los colores en la solución anterior corresponden a las flechas en la Figura 6.
El ejemplo de viga de pandeo del que hablamos anteriormente es un ejemplo de bifurcación en horquilla (quizás sería más apropiado llamarla "trifurcación"). La horquilla "ideal" se muestra a la izquierda de la Figura 7, dada por
y r = 0 es donde ocurre la bifurcación, representada por el punto negro en el origen de la Figura 8. A medida que r aumenta más allá de 0, el punto negro se divide en tres trayectorias: el punto fijo estable azul que se mueve hacia la derecha, el punto estable rojo que se mueve hacia la izquierda y un tercer punto inestable que permanece en el origen. Las líneas azul y roja son líneas continuas en la Figura 7 (izquierda), mientras que la trayectoria inestable negra es la parte punteada a lo largo del eje x positivo.
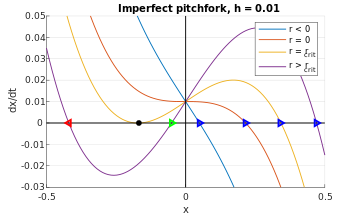
Como antes, considere un término de error h , donde 0 < h << 1, es decir

Una vez más, los retratos de fase se trasladan hacia arriba una cantidad infinitesimal, como se muestra en la Figura 9. El seguimiento de las intersecciones con el eje x en el diagrama de fase a medida que r cambia produce los puntos fijos, que recapitulan el resultado cualitativo de la Figura 7 (derecha). Más específicamente, el punto fijo azul de la Figura 9 corresponde a la trayectoria superior en la Figura 7 (derecha); el punto fijo verde es la trayectoria punteada; y el punto fijo rojo es la trayectoria más baja. Por lo tanto, en el caso imperfecto ( h ≠ 0), la bifurcación en horquilla se simplifica en un único punto fijo estable acoplado con una bifurcación en nodo de silla.
También se puede realizar un análisis de estabilidad lineal, excepto que se utiliza la solución generalizada para una ecuación cúbica en lugar de una cuadrática. El proceso es el mismo: 1) se establece la ecuación diferencial en cero y se encuentra la forma analítica de los puntos fijos x* , 2) se sustituye cada x* por la primera derivada y luego 3) se evalúa la estabilidad en función de si es positiva o negativa.
Las bifurcaciones combinadas de nodos en silla de montar en un sistema pueden generar multiestabilidad . La biestabilidad (un caso especial de multiestabilidad) es una propiedad importante en muchos sistemas biológicos, a menudo el resultado de una arquitectura de red que contiene una mezcla de interacciones de retroalimentación positiva y elementos ultrasensibles . Los sistemas biestables son histeréticos , es decir, el estado del sistema depende del historial de entradas, lo que puede ser crucial para el control de los procesos celulares como si se tratara de un interruptor. [2] Por ejemplo, esto es importante en contextos en los que una célula decide si comprometerse con una vía particular; una respuesta no histerética podría encender y apagar el sistema rápidamente cuando está sujeto a fluctuaciones térmicas aleatorias cercanas al umbral de activación, lo que puede ser ineficiente en términos de recursos.
Las redes con bifurcación en su dinámica controlan muchas transiciones importantes en el ciclo celular . Las transiciones G1/S , G2/M y Metafase-Anafase actúan como interruptores bioquímicos en el ciclo celular . Por ejemplo, los extractos de óvulos de Xenopus laevis entran y salen de la mitosis de manera irreversible por retroalimentación positiva en la fosforilación de Cdc2, una quinasa dependiente de ciclina . [3]
En ecología de poblaciones , la dinámica de las redes de interacciones de la red alimentaria puede presentar bifurcaciones de Hopf . Por ejemplo, en un sistema acuático que consta de un productor primario , un recurso mineral y un herbívoro, los investigadores descubrieron que los patrones de equilibrio, ciclado y extinción de poblaciones se podían describir cualitativamente con un modelo no lineal simple con una bifurcación de Hopf. [4]
La utilización de galactosa en la levadura en ciernes (S. cerevisiae) se puede medir a través de la expresión de GFP inducida por el promotor GAL en función de los cambios en las concentraciones de galactosa. El sistema exhibe un cambio biestable entre estados inducidos y no inducidos. [5]
De manera similar, la utilización de lactosa en E. coli en función de la concentración de tio-metilgalactósido (un análogo de la lactosa) medida por un promotor lac que expresa GFP exhibe biestabilidad e histéresis (Figura 10, izquierda y derecha respectivamente). [6]