Estimador minimax

En la teoría de la decisión estadística , cuando nos enfrentamos al problema de estimar un parámetro determinista (vector) a partir de observaciones, un estimador (regla de estimación) se denomina minimax si su riesgo máximo es mínimo entre todos los estimadores de . En cierto sentido, esto significa que es un estimador que funciona mejor en el peor caso posible permitido en el problema. ${\displaystyle \theta \in \Theta }$ ${\displaystyle x\in {\mathcal {X}},}$ ${\displaystyle \delta ^{M}\,\!}$ ${\displaystyle \theta \,\!}$ ${\displaystyle \delta ^{M}\,\!}$

Configuración del problema

Considere el problema de estimar un parámetro determinista (no bayesiano ) a partir de datos ruidosos o corruptos relacionados a través de la distribución de probabilidad condicional . Nuestro objetivo es encontrar un estimador "bueno" para estimar el parámetro , que minimice una función de riesgo dada . Aquí la función de riesgo (técnicamente un Funcional u Operador ya que es una función de una función, NO una composición de funciones) es la expectativa de alguna función de pérdida con respecto a . Un ejemplo popular para una función de pérdida ^[1] es la pérdida de error al cuadrado , y la función de riesgo para esta pérdida es el error cuadrático medio (MSE). ${\displaystyle \theta \in \Theta }$ ${\displaystyle x\in {\mathcal {X}}}$ ${\displaystyle P(x\mid \theta )\,\!}$ ${\displaystyle \delta (x)\,\!}$ ${\displaystyle \theta \,\!}$ ${\displaystyle R(\theta ,\delta )\,\!}$ ${\displaystyle R}$ ${\displaystyle L(\theta ,\delta )\,\!}$ ${\displaystyle P(x\mid \theta )\,\!}$ ${\displaystyle L(\theta ,\delta )=\|\theta -\delta \|^{2}\,\!}$

Lamentablemente, en general, el riesgo no se puede minimizar, ya que depende del parámetro desconocido en sí (si supiéramos cuál es el valor real de , no necesitaríamos estimarlo). Por lo tanto, se requieren criterios adicionales para encontrar un estimador óptimo en algún sentido. Uno de esos criterios es el criterio minimax. ${\displaystyle \theta \,\!}$ ${\displaystyle \theta \,\!}$

Definición

Definición  : Un estimador se denomina minimax con respecto a una función de riesgo si logra el riesgo máximo más pequeño entre todos los estimadores, lo que significa que satisface ${\displaystyle \delta ^{M}:{\mathcal {X}}\rightarrow \Theta \,\!}$ ${\displaystyle R(\theta ,\delta )\,\!}$

${\displaystyle \sup _{\theta \in \Theta }R(\theta ,\delta ^{M})=\inf _{\delta }\sup _{\theta \in \Theta }R(\theta ,\delta ).\,}$

Distribución menos favorable

Lógicamente, un estimador es minimax cuando es el mejor en el peor caso. Siguiendo esta lógica, un estimador minimax debería ser un estimador de Bayes con respecto a una distribución previa menos favorable de . Para demostrar esta noción, denotemos el riesgo promedio del estimador de Bayes con respecto a una distribución previa como ${\displaystyle \theta \,\!}$ ${\displaystyle \delta _{\pi }\,\!}$ ${\displaystyle \pi \,\!}$

${\displaystyle r_{\pi }=\int R(\theta ,\delta _{\pi })\,d\pi (\theta )\,}$

Definición: Una distribución previa se denomina menos favorable si para cualquier otra distribución el riesgo promedio satisface . ${\displaystyle \pi \,\!}$ ${\displaystyle \pi '\,\!}$ ${\displaystyle r_{\pi }\geq r_{\pi '}\,}$

Teorema 1: Si entonces: ${\displaystyle r_{\pi }=\sup _{\theta }R(\theta ,\delta _{\pi }),\,}$

1. ${\displaystyle \delta _{\pi }\,\!}$es minimax.
2. Si es un estimador Bayes único, también es el estimador minimax único. ${\displaystyle \delta _{\pi }\,\!}$
3. ${\displaystyle \pi \,\!}$es menos favorable.

Corolario: si un estimador bayesiano tiene riesgo constante, es minimax. Nótese que esta no es una condición necesaria.

Ejemplo 1: Moneda injusta ^{[2] [3]} : Consideremos el problema de estimar la tasa de "éxito" de una variable binomial , . Esto puede verse como estimar la tasa a la que una moneda injusta cae en "cara" o "cruz". En este caso, el estimador de Bayes con respecto a una distribución previa Beta , es ${\displaystyle x\sim B(n,\theta )\,\!}$ ${\displaystyle \theta \sim {\text{Beta}}({\sqrt {n}}/2,{\sqrt {n}}/2)\,}$

${\displaystyle \delta ^{M}={\frac {x+0.5{\sqrt {n}}}{n+{\sqrt {n}}}},\,}$

con riesgo bayesiano constante

${\displaystyle r={\frac {1}{4(1+{\sqrt {n}})^{2}}}\,}$

y, según el Corolario, es minimax.

Definición: Una secuencia de distribuciones previas se denomina menos favorable si para cualquier otra distribución , ${\displaystyle \pi _{n}\,\!}$ ${\displaystyle \pi '\,\!}$

${\displaystyle \lim _{n\rightarrow \infty }r_{\pi _{n}}\geq r_{\pi '}.\,}$

Teorema 2: Si existe una secuencia de valores anteriores y un estimador tal que , entonces : ${\displaystyle \pi _{n}\,\!}$ ${\displaystyle \delta \,\!}$ ${\displaystyle \sup _{\theta }R(\theta ,\delta )=\lim _{n\rightarrow \infty }r_{\pi _{n}}\,\!}$

1. ${\displaystyle \delta \,\!}$es minimax.
2. La secuencia es menos favorable. ${\displaystyle \pi _{n}\,\!}$

Tenga en cuenta que aquí no se garantiza la unicidad. Por ejemplo, el estimador ML del ejemplo anterior puede obtenerse como el límite de los estimadores de Bayes con respecto a una distribución previa uniforme , con un apoyo creciente, y también con respecto a una distribución previa normal de media cero con una varianza creciente. Por lo tanto, ni el estimador ML resultante es un minimax único ni la distribución previa menos favorable es única. ${\displaystyle \pi _{n}\sim U[-n,n]\,\!}$ ${\displaystyle \pi _{n}\sim N(0,n\sigma ^{2})\,\!}$

Ejemplo 2: Considere el problema de estimar la media de un vector aleatorio gaussiano dimensional , . El estimador de máxima verosimilitud (ML) para en este caso es simplemente , y su riesgo es ${\displaystyle p\,\!}$ ${\displaystyle x\sim N(\theta ,I_{p}\sigma ^{2})\,\!}$ ${\displaystyle \theta \,\!}$ ${\displaystyle \delta _{\text{ML}}=x\,\!}$

${\displaystyle R(\theta ,\delta _{\text{ML}})=E{\|\delta _{ML}-\theta \|^{2}}=\sum _{i=1}^{p}E(x_{i}-\theta _{i})^{2}=p\sigma ^{2}.\,}$

MSE del estimador de máxima verosimilitud frente al estimador de James-Stein

El riesgo es constante, pero el estimador ML en realidad no es un estimador de Bayes, por lo que el Corolario del Teorema 1 no se aplica. Sin embargo, el estimador ML es el límite de los estimadores de Bayes con respecto a la secuencia anterior y, por lo tanto, de hecho minimax según el Teorema 2. No obstante, la minimaxidad no siempre implica admisibilidad . De hecho, en este ejemplo, se sabe que el estimador ML es inadmisible (no admisible) siempre que . El famoso estimador de James-Stein domina al ML siempre que . Aunque ambos estimadores tienen el mismo riesgo cuando , y ambos son minimax, el estimador de James-Stein tiene un riesgo menor para cualquier finito . Este hecho se ilustra en la siguiente figura. ${\displaystyle \pi _{n}\sim N(0,n\sigma ^{2})\,\!}$ ${\displaystyle p>2\,\!}$ ${\displaystyle p>2\,\!}$ ${\displaystyle p\sigma ^{2}\,\!}$ ${\displaystyle \|\theta \|\rightarrow \infty \,\!}$ ${\displaystyle \|\theta \|\,\!}$

Algunos ejemplos

En general, es difícil, y a menudo incluso imposible, determinar el estimador minimax. No obstante, en muchos casos se ha determinado un estimador minimax.

Ejemplo 3: Media normal acotada: Al estimar la media de un vector normal , donde se sabe que . Se sabe que el estimador de Bayes con respecto a una distribución previa uniforme en el borde de la esfera acotada es minimax siempre que . La expresión analítica para este estimador es ${\displaystyle x\sim N(\theta ,I_{n}\sigma ^{2})\,\!}$ ${\displaystyle \|\theta \|^{2}\leq M\,\!}$ ${\displaystyle M\leq n\,\!}$

${\displaystyle \delta ^{M}(x)={\frac {MJ_{n+1}(M\|x\|)}{\|x\|J_{n}(M\|x\|)}}x,\,}$

donde , es la función de Bessel modificada del primer tipo de orden  n . ${\displaystyle J_{n}(t)\,\!}$

Estimador minimax asintótico

La dificultad de determinar el estimador minimax exacto ha motivado el estudio de estimadores de minimax asintóticos: un estimador se llama minimax asintótico (o aproximado) si ${\displaystyle \delta '}$ ${\displaystyle c}$

${\displaystyle \sup _{\theta \in \Theta }R(\theta ,\delta ')\leq c\inf _{\delta }\sup _{\theta \in \Theta }R(\theta ,\delta ).}$

Para muchos problemas de estimación, especialmente en el contexto de la estimación no paramétrica, se han establecido varios estimadores minimax aproximados. El diseño del estimador minimax aproximado está íntimamente relacionado con la geometría, como el número de entropía métrica, de . ${\displaystyle \Theta }$

Estimador minimax aleatorio

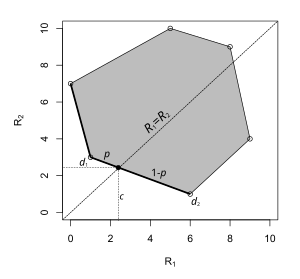
A veces, un estimador minimax puede adoptar la forma de una regla de decisión aleatoria . A la izquierda se muestra un ejemplo. El espacio de parámetros tiene solo dos elementos y cada punto del gráfico corresponde al riesgo de una regla de decisión: la coordenada x es el riesgo cuando el parámetro es y la coordenada y es el riesgo cuando el parámetro es . En este problema de decisión, el estimador minimax se encuentra en un segmento de línea que conecta dos estimadores deterministas. Elegir con probabilidad y con probabilidad minimiza el riesgo supremo. ${\displaystyle \theta _{1}}$ ${\displaystyle \theta _{2}}$ ${\displaystyle \delta _{1}}$ ${\displaystyle 1-p}$ ${\displaystyle \delta _{2}}$ ${\displaystyle p}$

Relación con la optimización robusta

La optimización robusta es un enfoque para resolver problemas de optimización bajo incertidumbre en el conocimiento de los parámetros subyacentes. ^{[4] [5]} Por ejemplo, la estimación bayesiana MMSE de un parámetro requiere el conocimiento de la función de correlación del parámetro. Si el conocimiento de esta función de correlación no está perfectamente disponible, un enfoque popular de optimización robusta minimax ^[6] es definir un conjunto que caracteriza la incertidumbre sobre la función de correlación y luego buscar una optimización minimax sobre el conjunto de incertidumbre y el estimador respectivamente. Se pueden buscar optimizaciones minimax similares para hacer que los estimadores sean robustos a ciertos parámetros conocidos de forma imprecisa. Por ejemplo, un estudio reciente que trata sobre tales técnicas en el área de procesamiento de señales se puede encontrar en. ^[7]

En R. Fandom Noubiap y W. Seidel (2001) se ha desarrollado un algoritmo para calcular una regla de decisión Gamma-minimax, cuando Gamma viene dada por un número finito de condiciones de momento generalizadas. Dicha regla de decisión minimiza el máximo de las integrales de la función de riesgo con respecto a todas las distribuciones en Gamma. Las reglas de decisión Gamma-minimax son de interés en los estudios de robustez en las estadísticas bayesianas.

Referencias

• EL Lehmann y G. Casella (1998), Teoría de la estimación puntual, 2.ª ed. Nueva York: Springer-Verlag.
• F. Perron y E. Marchand (2002), "Sobre el estimador minimax de una media normal acotada", Statistics and Probability Letters 58 : 327–333.
• R. Fandom Noubiap y W. Seidel (2001), "Un algoritmo para calcular reglas de decisión Gamma-Minimax bajo condiciones de momento generalizadas", Annals of Statistics , agosto de 2001, vol. 29, núm. 4, págs. 1094-1116
• Stein, C. (1981). "Estimación de la media de una distribución normal multivariante". Anales de Estadística . 9 (6): 1135–1151. doi : 10.1214/aos/1176345632 . MR  0630098. Zbl  0476.62035.

1. Berger, JO (1985). Teoría de la decisión estadística y análisis bayesiano (2.ª ed.). Nueva York: Springer-Verlag . pp. xv+425. ISBN. 0-387-96098-8.Sr. 0580664  .
2. Hodges, Jr., JL; Lehmann, EL (1950). "Algunos problemas en la estimación puntual minimax". Ann. Math. Statist . 21 (2): 182–197. doi : 10.1214/aoms/1177729838 . JSTOR  2236900. MR  0035949. Zbl  0038.09802.
3. Steinhaus, Hugon (1957). "El problema de la estimación". Ana. Matemáticas. Estatista . 28 (3): 633–648. doi : 10.1214/aoms/1177706876 . JSTOR  2237224. SEÑOR  0092313. Zbl  0088.35503.
4. SA Kassam y HV Poor (1985), "Técnicas robustas para el procesamiento de señales: un estudio", Actas del IEEE , vol. 73, págs. 433–481, marzo de 1985.
5. A. Ben-Tal, L. El Ghaoui y A. Nemirovski (2009), "Optimización robusta", Princeton University Press, 2009.
6. S. Verdu y HV Poor (1984), "Sobre la robustez Minimax: un enfoque general y aplicaciones", IEEE Transactions on Information Theory , vol. 30, págs. 328–340, marzo de 1984.
7. M. Danish Nisar. Robustez minimáxima en el procesamiento de señales para comunicaciones, Shaker Verlag, ISBN 978-3-8440-0332-1 , agosto de 2011.