Triangulación de Delaunay

En geometría computacional , una triangulación de Delaunay o triangulación de Delone de un conjunto de puntos en el plano subdivide su casco convexo ^[1] en triángulos cuyos círculos circunstantes no contienen ninguno de los puntos. Esto maximiza el tamaño del ángulo más pequeño en cualquiera de los triángulos y tiende a evitar los triángulos plateados .

La triangulación lleva el nombre de Boris Delaunay por su trabajo en ella desde 1934. ^[2]

Si todos los puntos se encuentran en una línea recta, la noción de triangulación se degenera y no existe una triangulación de Delaunay. Para cuatro o más puntos en el mismo círculo (por ejemplo, los vértices de un rectángulo), la triangulación de Delaunay no es única: cada una de las dos triangulaciones posibles que dividen el cuadrilátero en dos triángulos satisface la "condición de Delaunay", es decir, el requisito de que los círculos circunstantes de todos los triángulos tienen interiores vacíos.

Al considerar esferas circunscritas, la noción de triangulación de Delaunay se extiende a tres dimensiones y superiores. Es posible realizar generalizaciones a métricas distintas a la distancia euclidiana . Sin embargo, en estos casos no se garantiza que una triangulación de Delaunay exista o sea única.

Relación con el diagrama de Voronoi

La triangulación de Delaunay de un conjunto de puntos discretos $P$ en posición general corresponde a la gráfica dual del diagrama de Voronoi para $P.$ Los circuncentros de los triángulos de Delaunay son los vértices del diagrama de Voronoi. En el caso 2D, los vértices de Voronoi están conectados a través de aristas, que pueden derivarse de las relaciones de adyacencia de los triángulos de Delaunay: si dos triángulos comparten una arista en la triangulación de Delaunay, sus circuncentros deben conectarse con una arista en la teselación de Voronoi. .

Los casos especiales en los que esta relación no se cumple o es ambigua incluyen casos como:

Tres o más puntos colineales , donde las circunferencias circunstantes son de radios infinitos .
Cuatro o más puntos en un círculo perfecto, donde la triangulación es ambigua y todos los circuncentros son trivialmente idénticos.
Los bordes del diagrama de Voronoi que van al infinito no están definidos por esta relación en el caso de un conjunto finito $P.$ Si la triangulación de Delaunay se calcula utilizando el algoritmo de Bowyer-Watson, entonces se deben ignorar los circuncentros de los triángulos que tienen un vértice común con el "súper" triángulo. Las aristas que van al infinito comienzan desde un circuncentro y son perpendiculares a la arista común entre el triángulo mantenido e ignorado.

d-dimensional Delaunay

Para un conjunto $P$ de puntos en el espacio euclidiano ( $d$ -dimensional) , una triangulación de Delaunay es una triangulación $DT($ $P$ $)$ tal que ningún punto en $P$ está dentro de la circun-hiperesfera de cualquier $d$ - simplex en $DT($ $P$ $)$ . Se sabe ^[2] que existe una triangulación de Delaunay única para $P$ si $P$ es un conjunto de puntos en posición general ; es decir, la cáscara afín de $P$ es $d$ -dimensional y ningún conjunto de $d$ $+ 2$ puntos en $P$ se encuentra en el límite de una bola cuyo interior no corta a $P.$

El problema de encontrar la triangulación de Delaunay de un conjunto de puntos en el espacio euclidiano $d$ -dimensional se puede convertir al problema de encontrar el casco convexo de un conjunto de puntos en el espacio ( $d$ $+ 1$ )-dimensional. Esto se puede hacer dando a cada punto $p$ una coordenada adicional igual a $|$ $pag$ $|$ $2$ , convirtiéndolo así en un hiperparaboloide (esto se denomina "levantamiento"); tomar el lado inferior del casco convexo (ya que la tapa del extremo superior mira hacia arriba, lejos del origen, y debe descartarse); y mapear de nuevo al espacio $d$ -dimensional eliminando la última coordenada. Así como la carcasa convexa es única, también lo es la triangulación, asumiendo que todas las facetas de la carcasa convexa son simples . Las facetas no simpliciales sólo ocurren cuando $d$ $+ 2$ de los puntos originales se encuentran en la misma $d$ - hiperesfera , es decir, los puntos no están en posición general. ^[3]

Propiedades

Sea $n$ el número de puntos y $d$ el número de dimensiones.

La unión de todos los simples en la triangulación es la cáscara convexa de los puntos.
La triangulación de Delaunay contiene ⁠ ⁠ $\textstyle O{\bigl (}n^{\lceil d/2\rceil }{\bigr )}$ simples. ^[4]
En el plano ( $d = 2$ ), si hay $b$ vértices en el casco convexo, entonces cualquier triangulación de los puntos tiene como máximo $2 n - 2 - b$ triángulos, más una cara exterior (ver característica de Euler ).
Si los puntos se distribuyen según un proceso de Poisson en el plano con intensidad constante, entonces cada vértice tiene en promedio seis triángulos circundantes. De manera más general, para el mismo proceso en $d$ dimensiones, el número promedio de vecinos es una constante que depende solo de $d$ . ^[5]
En el plano, la triangulación de Delaunay maximiza el ángulo mínimo. En comparación con cualquier otra triangulación de puntos, el ángulo más pequeño en la triangulación de Delaunay es al menos tan grande como el ángulo más pequeño en cualquier otra. Sin embargo, la triangulación de Delaunay no necesariamente minimiza el ángulo máximo. ^[6] La triangulación de Delaunay tampoco necesariamente minimiza la longitud de los bordes.
Un círculo que circunscribe cualquier triángulo de Delaunay no contiene ningún otro punto de entrada en su interior.
Si un círculo que pasa por dos de los puntos de entrada no contiene ningún otro punto de entrada en su interior, entonces el segmento que conecta los dos puntos es una arista de una triangulación de Delaunay de los puntos dados.
Cada triángulo de la triangulación de Delaunay de un conjunto de puntos en espacios $d$ -dimensionales corresponde a una faceta de casco convexo de la proyección de los puntos sobre un paraboloide ( $d + 1$ )-dimensional , y viceversa.
El vecino más cercano $b$ a cualquier punto $p$ está en una arista $bp$ en la triangulación de Delaunay ya que el gráfico vecino más cercano es un subgrafo de la triangulación de Delaunay.
La triangulación de Delaunay es una llave geométrica : en el plano ( $d = 2$ ), se sabe que el camino más corto entre dos vértices, a lo largo de los bordes de Delaunay, no mide más de 1,998 veces la distancia euclidiana entre ellos. ^[7]

Definición de Visual Delaunay: Voltear

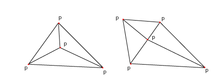
De las propiedades anteriores surge una característica importante: mirando dos triángulos $△ ABD, △ BCD$ con el borde común $BD$ (ver figuras), si la suma de los ángulos $α + γ \leq 180°$ , los triángulos cumplen la condición de Delaunay.

Esta es una propiedad importante porque permite el uso de una técnica de volteo . Si dos triángulos no cumplen la condición de Delaunay, cambiar la arista común $BD$ por la arista común $AC$ produce dos triángulos que sí cumplen la condición de Delaunay:

Esta triangulación no cumple la condición de Delaunay (la suma de $α$ y $γ$ es mayor que 180°).
Este par de triángulos no cumple la condición de Delaunay (hay un punto dentro del interior del círculo circunstante).
Al invertir el borde común se produce una triangulación de Delaunay válida para los cuatro puntos.

Esta operación se llama voltear y se puede generalizar a tres dimensiones o más. ^[8]

Algoritmos

Muchos algoritmos para calcular triangulaciones de Delaunay se basan en operaciones rápidas para detectar cuándo un punto está dentro del círculo circunstante de un triángulo y en una estructura de datos eficiente para almacenar triángulos y aristas. En dos dimensiones, una forma de detectar si el punto $D$ se encuentra en la circunferencia circunscrita de $A, B, C$ es evaluar el determinante : ^[9]

{\begin{aligned}&{\begin{vmatrix}A_{x}&A_{y}&A_{x}^{2}+A_{y}^{2}&1\\B_{x}&B_{ y}&B_{x}^{2}+B_{y}^{2}&1\\C_{x}&C_{y}&C_{x}^{2}+C_{y}^{2}&1\\ D_{x}&D_{y}&D_{x}^{2}+D_{y}^{2}&1\end{vmatrix}}\\[8pt]={}&{\begin{vmatrix}A_{x }-D_{x}&A_{y}-D_{y}&(A_{x}-D_{x})^{2}+(A_{y}-D_{y})^{2}\\B_ {x}-D_{x}&B_{y}-D_{y}&(B_{x}-D_{x})^{2}+(B_{y}-D_{y})^{2}\ \C_{x}-D_{x}&C_{y}-D_{y}&(C_{x}-D_{x})^{2}+(C_{y}-D_{y})^{2 }\end{vmatrix}}>0\end{aligned}}

Cuando $A, B, C$ se ordenan en sentido antihorario , este determinante es positivo sólo si $D$ se encuentra dentro del círculo circunstante.

Algoritmos de inversión

Como se mencionó anteriormente, si un triángulo no es Delaunay, podemos voltear uno de sus lados. Esto conduce a un algoritmo sencillo: construir cualquier triangulación de los puntos y luego invertir los bordes hasta que ningún triángulo no sea de Delaunay. Desafortunadamente, esto puede requerir $Ω(n 2)$ cambios de borde. ^[10] Si bien este algoritmo se puede generalizar a tres dimensiones o más, su convergencia no está garantizada en estos casos, ya que está condicionada a la conectividad del flip gráfico subyacente : este gráfico está conectado para conjuntos de puntos bidimensionales, pero Se puede desconectar en dimensiones superiores. ^[8]

incremental

La forma más sencilla de calcular eficientemente la triangulación de Delaunay es agregar repetidamente un vértice a la vez, retriangulando las partes afectadas del gráfico. Cuando se agrega un vértice $v$ , dividimos en tres el triángulo que contiene $v$ , luego aplicamos el algoritmo de inversión. Hecho de manera ingenua, esto tomará $O(n)$ tiempo: buscamos en todos los triángulos para encontrar el que contiene $v$ y luego, potencialmente, descartamos cada triángulo. Entonces el tiempo de ejecución general es $O(n 2)$ .

Si insertamos vértices en orden aleatorio, resulta (mediante una prueba un tanto compleja) que cada inserción invertirá, en promedio, sólo $O(1)$ triángulos, aunque a veces invertirá muchos más. ^[11] Esto todavía deja que el tiempo de ubicación del punto mejore. Podemos almacenar el historial de las divisiones y volteos realizados: cada triángulo almacena un puntero a los dos o tres triángulos que lo reemplazaron. Para encontrar el triángulo que contiene $v$ , comenzamos en una raíz de triángulo y seguimos el puntero que apunta a un triángulo que contiene $v$ , hasta encontrar un triángulo que aún no ha sido reemplazado. En promedio, esto también llevará $O(log n)$ tiempo. Entonces, en todos los vértices, esto lleva $O(n log n)$ tiempo. ^[12] Si bien la técnica se extiende a una dimensión superior (como lo demostraron Edelsbrunner y Shah ^[13] ), el tiempo de ejecución puede ser exponencial en la dimensión incluso si la triangulación final de Delaunay es pequeña.

El algoritmo Bowyer-Watson proporciona otro enfoque para la construcción incremental. Ofrece una alternativa al cambio de bordes para calcular los triángulos de Delaunay que contienen un vértice recién insertado.

Desafortunadamente, los algoritmos basados en volteos generalmente son difíciles de paralelizar, ya que agregar algún punto determinado (por ejemplo, el punto central de una rueda de carro) puede conducir a hasta $O(n)$ volteos consecutivos. Blelloch et al. ^[14] propusieron otra versión del algoritmo incremental basado en rip-and-tent, que es práctico y altamente paralelizado con un intervalo polilogarítmico .

Divide y conquistaras

Lee y Schachter desarrollaron un algoritmo de divide y vencerás para triangulaciones en dos dimensiones y lo mejoraron Guibas y Stolfi ^[9]^[15] y más tarde Dwyer. ^[16] En este algoritmo, se dibuja recursivamente una línea para dividir los vértices en dos conjuntos. La triangulación de Delaunay se calcula para cada conjunto y luego los dos conjuntos se fusionan a lo largo de la línea de división. Usando algunos trucos ingeniosos, la operación de fusión se puede realizar en el tiempo $O(n)$ , por lo que el tiempo total de ejecución es $O(n log n)$ . ^[17]

Para ciertos tipos de conjuntos de puntos, como una distribución aleatoria uniforme, al seleccionar inteligentemente las líneas de división, el tiempo esperado se puede reducir a $O (n log log n)$ y al mismo tiempo mantener el rendimiento en el peor de los casos.

Un paradigma de divide y vencerás para realizar una triangulación en $d$ dimensiones se presenta en "DeWall: Un rápido algoritmo de triangulación de divide y vencerás de Delaunay en E ^d " por P. Cignoni, C. Montani, R. Scopigno. ^[18]

Se ha demostrado que el algoritmo divide y vencerás es la técnica de generación secuencial de DT más rápida. ^[19]^[20]

casco de barrido

Sweephull ^[21] es una técnica híbrida para la triangulación de Delaunay 2D que utiliza un casco de barrido que se propaga radialmente y un algoritmo de inversión. El casco de barrido se crea secuencialmente iterando un conjunto de puntos 2D ordenados radialmente y conectando triángulos a la parte visible del casco convexo, lo que proporciona una triangulación que no se superpone. Se puede construir un casco convexo de esta manera siempre que el orden de los puntos garantice que ningún punto caiga dentro del triángulo. Pero la clasificación radial debería minimizar el volteo siendo altamente Delaunay para empezar. Luego, esto se combina con un paso final iterativo de inversión del triángulo.

Aplicaciones

El árbol de expansión mínimo euclidiano de un conjunto de puntos es un subconjunto de la triangulación de Delaunay de los mismos puntos, ^[22] y esto puede aprovecharse para calcularlo de manera eficiente.

Para modelar terreno u otros objetos dada una nube de puntos , la triangulación de Delaunay proporciona un buen conjunto de triángulos para usar como polígonos en el modelo. En particular, la triangulación de Delaunay evita triángulos estrechos (ya que tienen círculos circunstantes grandes en comparación con su área). Ver red irregular triangulada .

Las triangulaciones de Delaunay se pueden utilizar para determinar la densidad o intensidad de los muestreos de puntos mediante el estimador de campo de teselación de Delaunay (DTFE) .

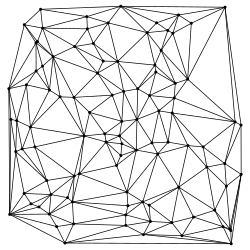
Las triangulaciones de Delaunay se utilizan a menudo para generar mallas para solucionadores discretizados en el espacio, como el método de elementos finitos y el método de simulación física de volúmenes finitos , debido a la garantía de ángulo y porque se han desarrollado algoritmos de triangulación rápidos. Normalmente, el dominio que se va a mallar se especifica como un complejo simplicial aproximado ; Para que la malla sea numéricamente estable, debe refinarse, por ejemplo utilizando el algoritmo de Ruppert .

La creciente popularidad de las técnicas del método de elementos finitos y del método de elementos de frontera aumenta el incentivo para mejorar los algoritmos de mallado automático. Sin embargo, todos estos algoritmos pueden crear elementos de cuadrícula distorsionados e incluso inutilizables. Afortunadamente, existen varias técnicas que pueden aprovechar una malla existente y mejorar su calidad. Por ejemplo, el suavizado (también conocido como refinamiento de malla) es uno de esos métodos, que reposiciona los nodos para minimizar la distorsión del elemento. El método de rejilla estirada permite generar mallas pseudoregulares que cumplen con los criterios de Delaunay de forma fácil y rápida en una solución de un solo paso.

La triangulación restringida de Delaunay ha encontrado aplicaciones en la planificación de rutas en la conducción automatizada y en los levantamientos topográficos. ^[23]

Ver también

esqueleto beta
Teselación centroidal de Voronoi
Algoritmos de casco convexo
Refinamiento Delaunay
Conjunto Delone , también conocido como conjunto Delaunay
Hiperuniformidad desordenada
Recorrido primero más lejano : inserción incremental de Voronoi
gabriel grafica
Calzada del Gigante
Análisis de patrón de gradiente
Encuadernado con Hamming – encuadernado con esferas
Algoritmo de Linde-Buzo-Gray
Algoritmo de Lloyd : iteración de Voronoi
conjunto meyer
Número de Pisot-Vijayaraghavan
Triangulación de Pitteway
plesioedro
Cuasicristal
Cuasitriangulación
número de salem
Punto de Steiner (triángulo)
Malla triangular
Gráfico de Urquhart
diagrama de voronói

Referencias

^ En términos generales, la región que encerraría una banda elástica estirada alrededor de los puntos.
^ ab Delaunay, Boris (1934). "Sur la sphère vide" [Sobre la esfera vacía]. Bulletin de l'Académie des Sciences de l'URSS, Classe des Sciences Mathématiques et Naturelles (en francés). 6 : 793–800.
^ Fukuda, Komei . "Preguntas frecuentes sobre computación poliédrica". www.cs.mcgill.ca . Consultado el 29 de octubre de 2018 .
^ Seidel, Raimund (1995). "El teorema del límite superior de los politopos: una prueba sencilla de su versión asintótica". Geometría Computacional . 5 (2): 115-116. doi :10.1016/0925-7721(95)00013-Y.
^ Meijering, JL (1953). "Área de interfaz, longitud de arista y número de vértices en agregados cristalinos con nucleación aleatoria" (PDF) . Informes de investigación de Philips . 8 : 270–290. Archivado desde el original (PDF) el 8 de marzo de 2017.Citado por Dwyer, Rex A. (1991). "Diagramas de Voronoĭ de dimensiones superiores en tiempo esperado lineal". Geometría Discreta y Computacional . 6 (4): 343–367. doi : 10.1007/BF02574694 . SEÑOR 1098813.
^ Edelsbrunner, Herbert ; Tan, Tiow Seng; Waupotitsch, romano (1992). "Un algoritmo de tiempo O (n2 log n) para la triangulación de ángulos minmax" (PDF) . Revista SIAM de Computación Científica y Estadística . 13 (4): 994–1008. CiteSeerX 10.1.1.66.2895 . doi :10.1137/0913058. SEÑOR 1166172. Archivado desde el original (PDF) el 9 de febrero de 2017 . Consultado el 24 de octubre de 2017 . .
^ Xia, Ge (2013). "El factor de estiramiento de la triangulación de Delaunay es inferior a 1,998". Revista SIAM de Computación . 42 (4): 1620–1659. arXiv : 1103.4361 . doi :10.1137/110832458. SEÑOR 3082502. S2CID 6646528.
^ ab De Loera, Jesús A .; Rambau, Jörg; Santos, Francisco (2010). Triangulaciones, Estructuras para Algoritmos y Aplicaciones . Algoritmos y Computación en Matemáticas. vol. 25. Saltador.
^ ab Guibas, Leónidas ; Stolfi, Jorge (1985). "Primitivas para la manipulación de subdivisiones generales y el cálculo de Voronoi". Transacciones ACM sobre gráficos . 4 (2): 74-123. doi : 10.1145/282918.282923 . S2CID 52852815.
^ Hurtado, F .; Noy, M.; Urrutia, J. (1999). "Cambiar los bordes de las triangulaciones". Geometría discreta y computacional . 22 (3): 333–346. doi : 10.1007/PL00009464 .
^ Guibas, Leónidas J .; Knuth, Donald E .; Sharir, Micha (1992). "Construcción incremental aleatoria de diagramas de Delaunay y Voronoi". Algorítmica . 7 (1–6): 381–413. doi :10.1007/BF01758770. S2CID 3770886.
^ de Berg, Marcos; Otfried Cheong ; Marc van Kreveld; Mark Overmars (2008). Geometría computacional: algoritmos y aplicaciones (PDF) . Springer-Verlag. ISBN 978-3-540-77973-5. Archivado desde el original (PDF) el 28 de octubre de 2009 . Consultado el 23 de febrero de 2010 .
^ Edelsbrunner, Herbert ; Shah, Nimish (1996). "Trabajos de inversión topológica incremental para triangulaciones regulares". Algorítmica . 15 (3): 223–241. doi :10.1007/BF01975867. S2CID 12976796.
^ Blelloch, chico; Gu, Yan; Evita, Julián; y Sun, Yihan. Paralelismo en algoritmos incrementales aleatorios Archivado el 25 de abril de 2018 en Wayback Machine . SPAA 2016. doi:10.1145/2935764.2935766.
^ Peterson, Samuel. "COMPUTACIÓN DE TRIANGULACIONES DE DELAUNAY CONSTRUIDAS EN EL AVIÓN". www.geom.uiuc.edu . Archivado desde el original el 22 de septiembre de 2017 . Consultado el 25 de abril de 2018 .
^ Dwyer, Rex A. (noviembre de 1987). "Un algoritmo más rápido de divide y vencerás para construir triangulaciones de Delaunay". Algorítmica . 2 (1–4): 137–151. doi :10.1007/BF01840356. S2CID 10828441.
^ Leach, G. (junio de 1992). "Mejora de los algoritmos de triangulación de Delaunay óptimos en el peor de los casos". 4ta Conferencia Canadiense sobre Geometría Computacional . CiteSeerX 10.1.1.56.2323 .
^ Cignoni, P.; C. Montani; R. Scopigno (1998). "DeWall: un rápido algoritmo de triangulación de Delaunay divide y vencerás en E ^d ". Diseño asistido por ordenador . 30 (5): 333–341. doi :10.1016/S0010-4485(97)00082-1.
^ Una comparación de algoritmos de triangulación secuencial de Delaunay "Copia archivada" (PDF) . Archivado desde el original (PDF) el 8 de marzo de 2012 . Consultado el 18 de agosto de 2010 .{{cite web}}: Mantenimiento CS1: copia archivada como título ( enlace )
^ "Algoritmos de triangulación y estructuras de datos". www.cs.cmu.edu . Archivado desde el original el 10 de octubre de 2017 . Consultado el 25 de abril de 2018 .
^ "Casco S" (PDF) . s-hull.org . Archivado (PDF) desde el original el 27 de octubre de 2013 . Consultado el 25 de abril de 2018 .
^ Franz Aurenhammer; Rolf Klein; Der-tsai Lee (26 de junio de 2013). Diagramas de Voronoi y triangulaciones de Delaunay. Compañía editorial científica mundial. págs.197–. ISBN 978-981-4447-65-2.
^ Sterling J. Anderson; Sisir B. Karumanchi; Karl Iagnemma (5 de julio de 2012). "Planificación y control basados en restricciones para el funcionamiento seguro y semiautónomo de vehículos" (PDF) . Simposio de vehículos inteligentes IEEE 2012 . IEEE. doi :10.1109/IVS.2012.6232153. Archivado desde el original (PDF) el 28 de febrero de 2019 . Consultado el 27 de febrero de 2019 .

enlaces externos

Triangulación de Delaunay en CGAL , la Biblioteca de Algoritmos de Geometría Computacional:
- Mariette Yvinec . Triangulación 2D. Consultado en abril de 2010.
- Pion, Sylvain; Teillaud, Monique . Triangulaciones 3D. Consultado en abril de 2010.
- Horno, Samuel; Devillers, Olivier; Jamín, Clemente. dD Triangulaciones.
- Hert, Susan; Seel, Michael. dD Cascos convexos y triangulaciones de Delaunay. Consultado en abril de 2010.
"Poly2Tri: triangulación incremental restringida de Delaunay. Implementación de C++ de código abierto. Consultado en abril de 2019.
"Construcción de triangulación Divide & Conquer Delaunay". Implementación de código abierto C99. Consultado en abril de 2019.
"CDT: triangulación de Delaunay restringida en C++". Implementación de C++ de código abierto. Consultado en agosto de 2022.