Fórmula para el área de un cuadrilátero
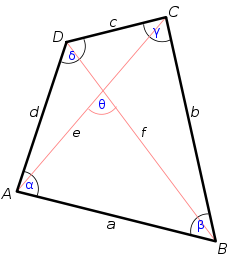
Un cuadrilátero. En geometría , la fórmula de Bretschneider es una expresión matemática para el área de un cuadrilátero general . Funciona tanto en cuadriláteros convexos como cóncavos (pero no en los cruzados), ya sean cíclicos o no.
Historia El matemático alemán Carl Anton Bretschneider descubrió la fórmula en 1842. La fórmula también fue derivada ese mismo año por el matemático alemán Karl Georg Christian von Staudt .
Formulación La fórmula de Bretschneider se expresa como:
K = ( s − a ) ( s − b ) ( s − do ) ( s − d ) − a b do d ⋅ porque 2 ( alfa + gamma 2 ) {\displaystyle K={\sqrt {(sa)(sb)(sc)(sd)-abcd\cdot \cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)}}} = ( s − a ) ( s − b ) ( s − do ) ( s − d ) − 1 2 a b do d [ 1 + porque ( alfa + gamma ) ] . {\displaystyle ={\sqrt {(sa)(sb)(sc)(sd)-{\tfrac {1}{2}}abcd[1+\cos(\alpha +\gamma )]}}.} Aquí, a b c d s semiperímetro y α γ porque ( alfa + gamma ) = porque ( β + del ) {\displaystyle \cos(\alpha +\gamma )=\cos(\beta +\delta )} alfa + β + gamma + del = 360 ∘ . {\displaystyle \alpha +\beta +\gamma +\delta =360^{\circ }.}
Prueba Denotamos el área del cuadrilátero por K
K = a d pecado alfa 2 + b do pecado gamma 2 . {\displaystyle {\begin{aligned}K&={\frac {ad\sin \alpha }{2}}+{\frac {bc\sin \gamma }{2}}.\end{aligned}}} Por lo tanto
2 K = ( a d ) pecado alfa + ( b do ) pecado gamma . {\displaystyle 2K=(ad)\sin \alpha +(bc)\sin \gamma .} 4 K 2 = ( a d ) 2 pecado 2 alfa + ( b do ) 2 pecado 2 gamma + 2 a b do d pecado alfa pecado gamma . {\displaystyle 4K^{2}=(ad)^{2}\sin ^{2}\alpha +(bc)^{2}\sin ^{2}\gamma +2abcd\sin \alpha \sin \gamma .} La ley de los cosenos implica que
a 2 + d 2 − 2 a d porque alfa = b 2 + do 2 − 2 b do porque gamma , {\displaystyle a^{2}+d^{2}-2ad\cos \alpha =b^{2}+c^{2}-2bc\cos \gamma,} porque ambos lados son iguales al cuadrado de la longitud de la diagonal BD
( a 2 + d 2 − b 2 − do 2 ) 2 4 = ( a d ) 2 porque 2 alfa + ( b do ) 2 porque 2 gamma − 2 a b do d porque alfa porque gamma . {\displaystyle {\frac {(a^{2}+d^{2}-b^{2}-c^{2})^{2}}{4}}=(ad)^{2}\cos ^{2}\alpha +(bc)^{2}\cos ^{2}\gamma -2abcd\cos \alpha \cos \gamma .} Agregando esto a la fórmula anterior para 4 K 2 se obtiene
4 K 2 + ( a 2 + d 2 − b 2 − c 2 ) 2 4 = ( a d ) 2 + ( b c ) 2 − 2 a b c d cos ( α + γ ) = ( a d + b c ) 2 − 2 a b c d − 2 a b c d cos ( α + γ ) = ( a d + b c ) 2 − 2 a b c d ( cos ( α + γ ) + 1 ) = ( a d + b c ) 2 − 4 a b c d ( cos ( α + γ ) + 1 2 ) = ( a d + b c ) 2 − 4 a b c d cos 2 ( α + γ 2 ) . {\displaystyle {\begin{aligned}4K^{2}+{\frac {(a^{2}+d^{2}-b^{2}-c^{2})^{2}}{4}}&=(ad)^{2}+(bc)^{2}-2abcd\cos(\alpha +\gamma )\\&=(ad+bc)^{2}-2abcd-2abcd\cos(\alpha +\gamma )\\&=(ad+bc)^{2}-2abcd(\cos(\alpha +\gamma )+1)\\&=(ad+bc)^{2}-4abcd\left({\frac {\cos(\alpha +\gamma )+1}{2}}\right)\\&=(ad+bc)^{2}-4abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right).\end{aligned}}} Nótese que: (una identidad trigonométrica verdadera para todos ) cos 2 α + γ 2 = 1 + cos ( α + γ ) 2 {\displaystyle \cos ^{2}{\frac {\alpha +\gamma }{2}}={\frac {1+\cos(\alpha +\gamma )}{2}}} α + γ 2 {\displaystyle {\frac {\alpha +\gamma }{2}}}
Siguiendo los mismos pasos que en la fórmula de Brahmagupta , esto se puede escribir como
16 K 2 = ( a + b + c − d ) ( a + b − c + d ) ( a − b + c + d ) ( − a + b + c + d ) − 16 a b c d cos 2 ( α + γ 2 ) . {\displaystyle 16K^{2}=(a+b+c-d)(a+b-c+d)(a-b+c+d)(-a+b+c+d)-16abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right).} Presentando el semiperímetro
s = a + b + c + d 2 , {\displaystyle s={\frac {a+b+c+d}{2}},} Lo anterior se convierte en
16 K 2 = 16 ( s − d ) ( s − c ) ( s − b ) ( s − a ) − 16 a b c d cos 2 ( α + γ 2 ) {\displaystyle 16K^{2}=16(s-d)(s-c)(s-b)(s-a)-16abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)} K 2 = ( s − a ) ( s − b ) ( s − c ) ( s − d ) − a b c d cos 2 ( α + γ 2 ) {\displaystyle K^{2}=(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)} y la fórmula de Bretschneider se deduce después de tomar la raíz cuadrada de ambos lados:
K = ( s − a ) ( s − b ) ( s − c ) ( s − d ) − a b c d ⋅ cos 2 ( α + γ 2 ) {\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cdot \cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)}}} La segunda forma se da utilizando la identidad del semiángulo del coseno.
cos 2 ( α + γ 2 ) = 1 + cos ( α + γ ) 2 , {\displaystyle \cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)={\frac {1+\cos \left(\alpha +\gamma \right)}{2}},} flexible
K = ( s − a ) ( s − b ) ( s − c ) ( s − d ) − 1 2 a b c d [ 1 + cos ( α + γ ) ] . {\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{2}}abcd[1+\cos(\alpha +\gamma )]}}.} Emmanuel García ha utilizado las fórmulas generalizadas de semiángulos para dar una prueba alternativa. [1]
Fórmulas relacionadas La fórmula de Bretschneider generaliza la fórmula de Brahmagupta para el área de un cuadrilátero cíclico , que a su vez generaliza la fórmula de Heron para el área de un triángulo .
El ajuste trigonométrico en la fórmula de Bretschneider para la no ciclicidad del cuadrilátero se puede reescribir de forma no trigonométrica en términos de los lados y las diagonales e f [2] [3]
K = 1 4 4 e 2 f 2 − ( b 2 + d 2 − a 2 − c 2 ) 2 = ( s − a ) ( s − b ) ( s − c ) ( s − d ) − 1 4 ( ( a c + b d ) 2 − e 2 f 2 ) = ( s − a ) ( s − b ) ( s − c ) ( s − d ) − 1 4 ( a c + b d + e f ) ( a c + b d − e f ) {\displaystyle {\begin{aligned}K&={\tfrac {1}{4}}{\sqrt {4e^{2}f^{2}-(b^{2}+d^{2}-a^{2}-c^{2})^{2}}}\\&={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{4}}((ac+bd)^{2}-e^{2}f^{2})}}\\&={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{4}}(ac+bd+ef)(ac+bd-ef)}}\\\end{aligned}}}
Notas ^ EA José García, Dos identidades y sus consecuencias, MATINF, 6 (2020) 5-11. [1] ^ Coolidge, JL (1939). "Una fórmula históricamente interesante para el área de un cuadrilátero". The American Mathematical Monthly . 46 (6): 345–347. doi :10.2307/2302891. JSTOR 2302891. ^ Hobson, EW (1918). Tratado sobre trigonometría plana. Cambridge University Press. págs. 204-205.
Referencias y lecturas adicionales Ayoub, Ayoub B. (2007). "Generalizaciones de los teoremas de Ptolomeo y Brahmagupta". Educación Matemática e Informática . 41 (1). ISSN 0730-8639. CA Bretschneider. Untersuchung der trigonometrischen Relationen des geradlinigen Viereckes. Archiv der Mathematik und Physik, Band 2, 1842, S. 225-261 (copia en línea, alemán) F. Strehlke: Zwei neue Sätze vom ebenen und sphärischen Viereck und Umkehrung des Ptolemaischen Lehrsatzes . Archiv der Mathematik und Physik, Band 2, 1842, S. 323-326 (copia en línea, alemán)
Enlaces externos