
 ) ( )
) ( )
 ) o pared- (
) o pared- ( ) vergencia ocular.
) vergencia ocular.Un autoestereograma es una imagen bidimensional (2D) que puede crear la ilusión óptica de una escena tridimensional (3D) . Los autoestereogramas utilizan solo una imagen para lograr el efecto, mientras que los estereogramas normales requieren dos. La escena 3D en un autoestereograma suele ser irreconocible hasta que se ve correctamente, a diferencia de los estereogramas típicos. Ver cualquier tipo de estereograma correctamente puede hacer que el espectador experimente un conflicto de convergencia-acomodación .
La ilusión óptica de un autoestereograma es una ilusión de percepción de profundidad e implica estereopsis : percepción de profundidad que surge de la perspectiva diferente que tiene cada ojo de una escena tridimensional, llamada paralaje binocular .
Las personas con visión binocular alterada y que no pueden percibir la profundidad pueden requerir un estereograma de movimiento para lograr un efecto similar.
El tipo más simple de autoestereograma consiste en un patrón que se repite horizontalmente, con pequeños cambios a lo largo de todo el texto, que parece un fondo de pantalla . Cuando se observa con la vergencia adecuada , los patrones repetidos parecen flotar por encima o por debajo del fondo. Los conocidos libros Magic Eye presentan otro tipo de autoestereograma llamado autoestereograma de puntos aleatorios ( ), similar al primer ejemplo, arriba. En este tipo de autoestereograma, cada píxel de la imagen se calcula a partir de una tira de patrón y un mapa de profundidad . Una escena 3D oculta emerge cuando la imagen se observa con la vergencia correcta.
A diferencia de los estereogramas normales, los autoestereogramas no requieren el uso de un estereoscopio . Un estereoscopio presenta imágenes en 2D del mismo objeto desde ángulos ligeramente diferentes para el ojo izquierdo y el ojo derecho, lo que permite al observador reconstruir el objeto original mediante disparidad binocular . Cuando se observa con la vergencia adecuada, un autoestereograma hace lo mismo, existiendo la disparidad binocular en partes adyacentes de los patrones 2D repetidos.
Hay dos formas de ver un autoestereograma: bizco y estrabismo . [a] La mayoría de los autoestereogramas (incluidos los de este artículo) están diseñados para verse de una sola manera, que suele ser bizco. La visión bizco requiere que los dos ojos adopten un ángulo relativamente paralelo , mientras que la visión bizco requiere un ángulo relativamente convergente . Una imagen diseñada para la visión bizco, si se ve correctamente, parecerá sobresalir del fondo, mientras que si se ve bizco, aparecerá como un recorte detrás del fondo y puede resultar difícil enfocarla por completo. [b]
En 1593, Giambattista della Porta vio una página de un libro con un ojo y otra página con el otro. Pudo leer una de las páginas, siendo la otra invisible, y cambiar "la virtud visual" para leer la otra página, volviéndose invisible la primera. [2] Este es un ejemplo temprano de disociar la vergencia de la acomodación, una capacidad necesaria para ver autoestereogramas. Sin embargo, Porta vio competencia entre las imágenes vistas por los dos ojos, rivalidad binocular .
No fue hasta 1838 cuando Charles Wheatstone publicó un ejemplo de cooperación entre las imágenes de los dos ojos: la estereopsis (percepción binocular de la profundidad). Explicó que la profundidad surgía de las diferencias en las posiciones horizontales de las imágenes en los dos ojos. Respaldó su explicación mostrando imágenes planas bidimensionales con tales diferencias horizontales, estereogramas , por separado a los ojos izquierdo y derecho a través de un estereoscopio que él inventó basado en espejos . A partir de tales pares de imágenes planas, las personas experimentaban la ilusión de profundidad. [3] [4]
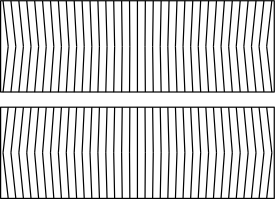
En 1844, David Brewster descubrió el «efecto papel tapiz». [5] Observó que cuando miraba patrones repetidos en papeles tapiz mientras variaba su vergencia, podía verlos detrás de la pared (con vergencia bizca) o delante de la pared (con vergencia bizca). [6] Esta es la base de los autoestereogramas de estilo papel tapiz. [3]
En 1939, Boris Kompaneysky [7] publicó el primer estereograma de puntos aleatorios que contenía una imagen dibujada a mano de la cara de Venus, [8] pensada para ser vista con un dispositivo.
En 1959, Bela Julesz , [9] [10] científico de la visión, psicólogo y miembro de MacArthur , inventó los estereogramas de puntos aleatorios mientras trabajaba en los Laboratorios Bell en el reconocimiento de objetos camuflados a partir de fotografías aéreas tomadas por aviones espía. En ese momento, muchos científicos de la visión asumieron que la estereopsis requería un análisis previo de los contornos visibles de las imágenes en cada ojo, pero Julesz demostró que ocurre con imágenes sin tales contornos visibles en cada uno de los ojos. Los contornos del objeto de profundidad se vuelven visibles solo después de que la estereopsis haya procesado las diferencias en las posiciones horizontales de los puntos en las imágenes de los dos ojos. [11] [12]
El diseñador japonés Masayuki Ito, siguiendo a Julesz, creó un estereograma de una sola imagen en 1970 y el pintor suizo Alfons Schilling creó un estereograma de una sola imagen hecho a mano en 1974, [8] después de crear más de un visor y reunirse con Julesz. [13] Al tener experiencia con imágenes estereoscópicas en holografía , fotografía lenticular y vectografía , desarrolló un método de puntos aleatorios basado en líneas verticales espaciadas estrechamente en paralaje. [14]
En 1979, Christopher Tyler del Instituto Smith-Kettlewell , un estudiante de Julesz y un psicofísico visual , combinó las teorías detrás de los estereogramas de papel tapiz de una sola imagen y los estereogramas de puntos aleatorios (el trabajo de Julesz y Schilling) para crear el primer autoestereograma de puntos aleatorios en blanco y negro con la ayuda de la programadora de computadoras Maureen Clarke usando Apple II y BASIC . [15] Stork y Rocca publicaron el primer artículo académico y proporcionaron software para generar estereogramas de puntos aleatorios. [16] Este tipo de autoestereograma permite a una persona ver formas 3D a partir de una sola imagen 2D sin la ayuda de equipo óptico. [17] [18] En 1991, el programador de computadoras Tom Baccei y la artista Cheri Smith crearon los primeros autoestereogramas de puntos aleatorios en color, posteriormente comercializados como Magic Eye . [19]
Ron Kimmel describió un procedimiento informático que extrae la geometría oculta de una imagen de autoestereograma . [20] Además del estereotipo clásico, agrega suavidad como un supuesto importante en la reconstrucción de la superficie.
A finales de los años 90, muchas revistas infantiles incluían estereogramas automáticos. Incluso revistas de videojuegos como Nintendo Power tenían una sección dedicada específicamente a estas ilusiones. Desde entonces, se han publicado varios libros, siendo Magic Eye Beyond 3D: Improve Your Vision una publicación clave que puso esta intrigante ilusión en el mercado.

La estereopsis , o visión estereoscópica, es la combinación visual de dos imágenes similares pero no idénticas en una sola, con la consiguiente percepción visual de solidez y profundidad . [21] [22] En el cerebro humano, la estereopsis resulta de mecanismos complejos que forman una impresión tridimensional al hacer coincidir cada punto (o conjunto de puntos) en la visión de un ojo con el punto (o conjunto de puntos) equivalente en la visión del otro ojo. Utilizando la disparidad binocular , el cerebro deriva las posiciones de los puntos en el eje z (profundidad), que de otro modo sería inescrutable.
Cuando se le presenta al cerebro un patrón repetitivo, como un papel tapiz , tiene dificultades para hacer coincidir con precisión las vistas de los dos ojos. Al mirar un patrón que se repite horizontalmente , pero haciendo converger los dos ojos en un punto detrás del patrón, es posible engañar al cerebro para que haga coincidir un elemento del patrón, como lo ve el ojo izquierdo, con otro elemento (de aspecto similar), al lado del primero, como lo ve el ojo derecho. Con la típica visión bizco, esto da la ilusión de un plano que tiene el mismo patrón pero está ubicado detrás de la pared real. La distancia a la que se encuentra este plano detrás de la pared depende solo del espaciamiento entre elementos idénticos. [23]
Los autoestereogramas utilizan esta dependencia de la profundidad con respecto al espaciado para crear imágenes tridimensionales. Si, en alguna zona de la imagen, el patrón se repite a distancias más pequeñas, esa zona aparecerá más cerca que el plano de fondo. Si la distancia de las repeticiones es mayor en alguna zona, entonces esa zona aparecerá más distante (como un agujero en el plano).

 )
)A las personas que nunca han podido percibir formas 3D ocultas en un autoestereograma les resulta difícil comprender comentarios como "la imagen 3D simplemente aparecerá en el fondo después de que se mire la imagen durante suficiente tiempo" o "los objetos 3D simplemente emergerán del fondo". Esto ayuda a ilustrar cómo las imágenes 3D "emergen" del fondo desde la perspectiva de un segundo observador. Si los objetos 3D virtuales reconstruidos por el cerebro del observador del autoestereograma fueran objetos reales, un segundo observador que observara la escena desde un costado vería estos objetos flotando en el aire sobre la imagen de fondo.
Los efectos 3D del autoestereograma de ejemplo se crean repitiendo los iconos del jinete del tigre cada 140 píxeles en el plano de fondo, los iconos del jinete del tiburón cada 130 píxeles en el segundo plano y los iconos del tigre cada 120 píxeles en el plano más alto. Cuanto más cerca se agrupan horizontalmente los iconos, más se elevan respecto del plano de fondo. Esta distancia de repetición se conoce como profundidad o valor del eje z de un patrón particular en el autoestereograma. El valor de profundidad también se conoce como valor del búfer Z.
El cerebro es capaz de hacer coincidir casi instantáneamente cientos de patrones repetidos a diferentes intervalos para recrear la información de profundidad correcta para cada patrón. Un autoestereograma puede contener unos 50 tigres de distintos tamaños, repetidos a diferentes intervalos sobre un fondo complejo y repetido. Sin embargo, a pesar de la aparente disposición caótica de los patrones, el cerebro es capaz de colocar cada icono de tigre en su profundidad adecuada. [ Se discute la neutralidad ]
Los autoestereogramas en los que los patrones de una fila particular se repiten horizontalmente con el mismo espaciado se pueden leer con los ojos bizcos o bizcos. En estos autoestereogramas, ambos tipos de lectura producirán una interpretación de profundidad similar, con la excepción de que la lectura bizca invierte la profundidad (las imágenes que antes sobresalían ahora se introducen).
Sin embargo, no es necesario que los iconos de una fila estén dispuestos a intervalos idénticos. Un autoestereograma con intervalos variables entre los iconos de una fila presenta estos iconos en diferentes planos de profundidad al espectador. La profundidad de cada icono se calcula a partir de la distancia entre él y su vecino de la izquierda. Este tipo de autoestereogramas están diseñados para ser leídos de una sola manera, ya sea bizcos o desviados. Todos los autoestereogramas de este artículo están codificados para ser vistos bizcos, a menos que se indique específicamente lo contrario. Un autoestereograma codificado para ser visto bizco producirá patrones inversos cuando se vea bizco, y viceversa. [b]
El autoestereograma de ejemplo de mapa de profundidad con ojos saltones que se muestra a la derecha codifica tres planos a lo largo del eje x . El plano de fondo está en el lado izquierdo de la imagen. El plano más alto se muestra en el lado derecho de la imagen. Hay un plano medio angosto en el medio del eje x . Comenzando con un plano de fondo donde los íconos están espaciados a 140 píxeles, se puede elevar un ícono en particular desplazándolo una cierta cantidad de píxeles hacia la izquierda. Por ejemplo, el plano medio se crea desplazando un ícono 10 píxeles hacia la izquierda, lo que crea efectivamente un espaciado que consta de 130 píxeles. El cerebro no depende de íconos inteligibles que representan objetos o conceptos. En este autoestereograma, los patrones se vuelven cada vez más pequeños a lo largo del eje y, hasta que parecen puntos aleatorios. El cerebro aún puede hacer coincidir estos patrones de puntos aleatorios.
La relación de distancia entre cualquier píxel y su contraparte en el patrón equivalente a la izquierda se puede expresar en un mapa de profundidad . Un mapa de profundidad es simplemente una imagen en escala de grises que representa la distancia entre un píxel y su contraparte izquierda utilizando un valor de escala de grises entre el blanco y el negro. [18] Por convención, cuanto más cercana es la distancia, más brillante se vuelve el color.
Con esta convención, se puede crear un mapa de profundidad en escala de grises para el autoestereograma de ejemplo, en el que el negro, el gris y el blanco representan desplazamientos de 0 píxeles, 10 píxeles y 20 píxeles, respectivamente, como se muestra en el autoestereograma de ejemplo en escala de grises. Un mapa de profundidad es la clave para la creación de autoestereogramas de puntos aleatorios.
Un programa informático puede tomar un mapa de profundidad y una imagen de patrón que lo acompaña para producir un autoestereograma. El programa coloca la imagen de patrón en mosaico horizontalmente para cubrir un área cuyo tamaño es idéntico al mapa de profundidad. Conceptualmente, en cada píxel de la imagen de salida, el programa busca el valor de escala de grises del píxel equivalente en la imagen del mapa de profundidad y utiliza este valor para determinar la cantidad de desplazamiento horizontal necesario para el píxel.
Una forma de lograr esto es hacer que el programa escanee cada línea de la imagen de salida píxel por píxel de izquierda a derecha. Inicializa la primera serie de píxeles de una fila a partir de la imagen del patrón. Luego consulta el mapa de profundidad para recuperar los valores de desplazamiento adecuados para los píxeles posteriores. Para cada píxel, resta el desplazamiento del ancho de la imagen del patrón para llegar a un intervalo de repetición. Utiliza este intervalo de repetición para buscar el color del píxel homólogo a la izquierda y utiliza su color como el color propio del nuevo píxel. [23]
A diferencia de los planos de profundidad simples creados por los autoestereogramas de papel tapiz simples, los cambios sutiles en el espaciado especificados por el mapa de profundidad pueden crear la ilusión de gradientes suaves en la distancia. Esto es posible porque el mapa de profundidad en escala de grises permite colocar píxeles individuales en uno de los 2 n planos de profundidad, donde n es la cantidad de bits que utiliza cada píxel en el mapa de profundidad. En la práctica, la cantidad total de planos de profundidad está determinada por la cantidad de píxeles utilizados para el ancho de la imagen del patrón. Cada valor de escala de grises debe traducirse al espacio de píxeles para poder desplazar los píxeles en el autoestereograma final. Como resultado, la cantidad de planos de profundidad debe ser menor que el ancho del patrón.

 )
)
El gradiente ajustado requiere una imagen de patrón más compleja que el papel tapiz estándar con patrón repetitivo, por lo que normalmente se utiliza un patrón que consiste en puntos aleatorios repetidos. Cuando se ve el autoestereograma con la técnica de visualización adecuada, surge una escena 3D oculta. Los autoestereogramas de este tipo se conocen como autoestereogramas de puntos aleatorios.
También se pueden lograr gradientes suaves con un patrón inteligible, suponiendo que el patrón sea lo suficientemente complejo y no tenga parches grandes, horizontales y monótonos. Una gran área pintada con un color monótono sin cambios en el tono y el brillo no se presta al desplazamiento de píxeles, ya que el resultado del desplazamiento horizontal es idéntico al parche original. El siguiente mapa de profundidad de un tiburón con gradiente suave produce un autoestereograma perfectamente legible, aunque la imagen 2D contiene pequeñas áreas monótonas; el cerebro es capaz de reconocer estos pequeños espacios y llenar los espacios en blanco ( contornos ilusorios ). Si bien se utilizan patrones inteligibles y repetidos en lugar de puntos aleatorios, este tipo de autoestereograma todavía es conocido por muchos como un autoestereograma de puntos aleatorios, porque se crea utilizando el mismo proceso.

 ) Haga clic aquí para la versión 800 × 400
) Haga clic aquí para la versión 800 × 400 Cuando se muestran una serie de autoestereogramas uno tras otro, de la misma manera que se muestran imágenes en movimiento , el cerebro percibe un autoestereograma animado . Si todos los autoestereogramas de la animación se producen utilizando el mismo patrón de fondo, a menudo es posible ver contornos tenues de partes del objeto 3D en movimiento en la imagen del autoestereograma 2D sin necesidad de mirar de reojo; los píxeles en constante movimiento del objeto en movimiento se pueden distinguir claramente del plano de fondo estático. Para eliminar este efecto secundario, los autoestereogramas animados a menudo utilizan un fondo cambiante para ocultar las partes en movimiento.
Cuando se ve un patrón repetitivo regular en un monitor CRT como si fuera un autoestereograma de fondo de pantalla, normalmente es posible ver ondulaciones de profundidad. Esto también se puede ver en el fondo de un autoestereograma estático de puntos aleatorios. Estas ondulaciones son causadas por los desplazamientos laterales de la imagen debido a pequeños cambios en la sensibilidad de deflexión (linealidad) del escaneo de línea, que luego se interpretan como profundidad. Este efecto es especialmente evidente en el borde izquierdo de la pantalla, donde la velocidad de escaneo aún se está estabilizando después de la fase de retorno. En una pantalla LCD TFT , que funciona de manera diferente, esto no ocurre y el efecto no está presente. Las pantallas CRT de mayor calidad también tienen mejor linealidad y exhiben menos o nada de este efecto.
Existen muchos consejos sobre cómo ver la imagen tridimensional deseada en un autoestereograma. Si bien algunas personas pueden ver rápidamente la imagen tridimensional en un autoestereograma con poco esfuerzo, otras deben aprender a entrenar sus ojos para disociar la convergencia ocular del enfoque de la lente.
No todas las personas pueden ver la ilusión 3D en los autoestereogramas. Debido a que los autoestereogramas se construyen en base a la visión estereoscópica , las personas con diversas discapacidades visuales, incluso aquellas que afectan solo un ojo, no pueden ver las imágenes tridimensionales.
Las personas con ambliopía (también conocida como ojo vago) no pueden ver imágenes tridimensionales. Los niños con visión deficiente o disfuncional durante un período crítico de la infancia pueden crecer estereociegos , ya que sus cerebros no son estimulados por imágenes estereoscópicas durante el período crítico. Si este problema de visión no se corrige en la primera infancia, el daño se vuelve permanente y el adulto nunca podrá ver estereogramas. [3] [c] Se estima que entre el 1 y el 5 por ciento de la población padece ambliopía. [25]
La percepción de profundidad es el resultado de muchas pistas visuales monoculares y binoculares. En el caso de objetos relativamente cercanos a los ojos, la visión binocular desempeña un papel importante en la percepción de profundidad. La visión binocular permite al cerebro crear una única imagen ciclópea y asignar un nivel de profundidad a cada punto de la misma. [11]
El cerebro utiliza el desplazamiento de coordenadas (también conocido como paralaje) de los objetos emparejados para identificar la profundidad de estos objetos. [23] El nivel de profundidad de cada punto en la imagen combinada se puede representar mediante un píxel en escala de grises en una imagen 2D, para beneficio del lector. Cuanto más cerca aparece un punto del cerebro, más brillante se pinta. Por lo tanto, la forma en que el cerebro percibe la profundidad mediante la visión binocular se puede capturar mediante un mapa de profundidad (imagen ciclópea) pintado en función del desplazamiento de coordenadas.


El ojo funciona como una cámara fotográfica. Tiene un iris ajustable que puede abrirse (o cerrarse) para permitir que entre más (o menos) luz en el ojo. Como sucede con cualquier cámara, excepto las estenopeicas , necesita enfocar los rayos de luz que entran por el iris (abertura de la cámara) de modo que se enfoquen en un único punto de la retina para producir una imagen nítida. El ojo logra este objetivo ajustando una lente detrás de la córnea para refractar la luz de forma adecuada.
La visión estereoscópica basada en el paralaje permite al cerebro calcular la profundidad de los objetos en relación con el punto de convergencia. Es el ángulo de convergencia el que proporciona al cerebro el valor de profundidad de referencia absoluto para el punto de convergencia a partir del cual se pueden inferir las profundidades absolutas de todos los demás objetos.

Los ojos normalmente enfocan y convergen a la misma distancia en un proceso conocido como convergencia acomodativa . Es decir, cuando se mira un objeto lejano, el cerebro automáticamente aplana las lentes y rota los dos globos oculares para ver con los ojos bizcos. Es posible entrenar al cerebro para que desacople estas dos operaciones. Este desacoplamiento no tiene ninguna utilidad en la vida cotidiana, porque impide que el cerebro interprete los objetos de manera coherente. Sin embargo, para ver una imagen hecha por humanos, como un autoestereograma donde los patrones se repiten horizontalmente, es crucial desacoplar el enfoque de la convergencia. [3]
Al enfocar las lentes en un autoestereograma cercano donde se repiten patrones y al hacer converger los globos oculares en un punto distante detrás de la imagen del autoestereograma, se puede engañar al cerebro para que vea imágenes en 3D. Si los patrones recibidos por los dos ojos son lo suficientemente similares, el cerebro considerará que estos dos patrones coinciden y los tratará como si vinieran del mismo objeto imaginario. Este tipo de visualización se conoce como visión bizca , porque los globos oculares adoptan una convergencia bizca en un plano distante, aunque la imagen del autoestereograma esté en realidad más cerca de los ojos. [23] Debido a que los dos globos oculares convergen en un plano más alejado, la ubicación percibida del objeto imaginario está detrás del autoestereograma. El objeto imaginario también parece más grande que los patrones en el autoestereograma debido al escorzo .
El siguiente autoestereograma muestra tres filas de patrones repetidos. Cada patrón se repite en un intervalo diferente para colocarlo en un plano de profundidad diferente. Las dos líneas que no se repiten se pueden utilizar para verificar la correcta visión bizco. Cuando el cerebro interpreta correctamente el autoestereograma utilizando la visión bizco y uno mira fijamente al delfín en el medio del campo visual, el cerebro debería ver dos conjuntos de líneas parpadeantes, como resultado de la rivalidad binocular . [11]

 )
)Aunque hay seis patrones de delfines en el autoestereograma, el cerebro debería ver siete delfines "aparentes" en el plano del autoestereograma. Este es un efecto secundario del emparejamiento de patrones similares por parte del cerebro. Hay cinco pares de patrones de delfines en esta imagen. Esto permite al cerebro crear cinco delfines aparentes. El patrón más a la izquierda y el más a la derecha por sí solos no tienen pareja, pero el cerebro intenta asimilar estos dos patrones en el plano de profundidad establecido de delfines adyacentes a pesar de la rivalidad binocular. Como resultado, hay siete delfines aparentes, y el más a la izquierda y el más a la derecha aparecen con un ligero parpadeo, no muy diferente a los dos conjuntos de líneas parpadeantes que se observan cuando uno mira fijamente al cuarto delfín aparente.
Debido al escorzo, la diferencia en la convergencia necesaria para ver patrones repetidos en diferentes planos hace que el cerebro atribuya tamaños diferentes a patrones con tamaños 2D idénticos. En el autoestereograma de tres filas de cubos, si bien todos los cubos tienen las mismas dimensiones físicas 2D, los de la fila superior parecen más grandes, porque se perciben como más alejados que los cubos de la segunda y tercera filas.

 )
)Si uno tiene dos ojos, una vista relativamente sana y no tiene problemas neurológicos que le impidan percibir la profundidad, entonces es capaz de aprender a ver las imágenes contenidas en los autoestereogramas. “Al igual que sucede cuando se aprende a andar en bicicleta o a nadar, algunos aprenden a hacerlo de inmediato, mientras que a otros les resulta más difícil”. [26]
Al igual que con una cámara fotográfica , es más fácil hacer que el ojo enfoque un objeto cuando hay una luz ambiental intensa. Con una iluminación intensa, el ojo puede contraer la pupila , pero permitir que llegue suficiente luz a la retina. Cuanto más se parezca el ojo a una cámara estenopeica , menos dependerá del enfoque a través de la lente . [d] En otras palabras, se reduce el grado de disociación entre el enfoque y la convergencia necesarios para visualizar un autoestereograma. Esto supone menos tensión para el cerebro. Por lo tanto, puede ser más fácil para quienes ven por primera vez un autoestereograma "ver" sus primeras imágenes en 3D si intentan esta hazaña con una iluminación brillante.
El control de la convergencia es importante para poder ver imágenes en 3D. Por lo tanto, puede resultar útil concentrarse en la convergencia/divergencia de los dos ojos para cambiar las imágenes que llegan a ambos ojos, en lugar de intentar ver una imagen clara y enfocada. Aunque el cristalino se ajusta de forma refleja para producir imágenes claras y enfocadas, es posible controlar voluntariamente este proceso. [27] En cambio, el observador alterna entre la convergencia y la divergencia de los dos ojos, y en el proceso ve "imágenes dobles" que se observan típicamente cuando uno está borracho o intoxicado de alguna otra manera. Finalmente, el cerebro logrará hacer coincidir con éxito un par de patrones informados por los dos ojos y se fijará en este grado particular de convergencia. El cerebro también ajustará los cristales oculares para obtener una imagen clara del par coincidente. Una vez hecho esto, las imágenes alrededor de los patrones coincidentes se vuelven claras rápidamente a medida que el cerebro combina patrones adicionales utilizando aproximadamente el mismo grado de convergencia.

 )
)
 )
)Cuando uno mueve su atención de un plano de profundidad a otro (por ejemplo, de la fila superior del tablero de ajedrez a la fila inferior), ambos ojos necesitan ajustar su convergencia para que coincida con el nuevo intervalo de repetición de patrones. Si el nivel de cambio en la convergencia es demasiado alto durante este cambio, a veces el cerebro puede perder la disociación que tanto le costó lograr entre el enfoque y la convergencia. Por lo tanto, para un espectador primerizo, puede ser más fácil ver el autoestereograma si ambos ojos ensayan el ejercicio de convergencia en un autoestereograma donde la profundidad de los patrones a lo largo de una fila particular permanece constante.
En un autoestereograma de puntos aleatorios, la imagen 3D se muestra generalmente en el centro del autoestereograma contra un plano de profundidad de fondo (véase el autoestereograma del tiburón). Puede resultar útil establecer la convergencia adecuada primero observando la parte superior o inferior del autoestereograma, donde los patrones se repiten generalmente a intervalos constantes. Una vez que el cerebro se fija en el plano de profundidad de fondo, tiene un grado de convergencia de referencia a partir del cual puede hacer coincidir los patrones en diferentes niveles de profundidad en el centro de la imagen.
La mayoría de los autoestereogramas, incluidos los de este artículo, están diseñados para la observación divergente (con los ojos bizcos). Una forma de ayudar al cerebro a concentrarse en la divergencia en lugar de enfocar es sostener la imagen frente a la cara, con la nariz tocando la imagen. Con la imagen tan cerca de los ojos, la mayoría de las personas no pueden enfocarla. El cerebro puede dejar de intentar mover los músculos oculares para obtener una imagen clara. Si uno aleja lentamente la imagen de la cara, mientras se abstiene de enfocar o rotar los ojos, en algún momento el cerebro se fijará en un par de patrones cuando la distancia entre ellos coincida con el grado de convergencia actual de los dos globos oculares. [17]
Otra forma es mirar fijamente un objeto detrás de la imagen en un intento de establecer la divergencia adecuada, mientras se mantiene una parte de la vista fija en la imagen para convencer al cerebro de que se centre en ella. Un método modificado consiste en que el espectador se centre en su reflejo en una superficie reflectante de la imagen, que el cerebro percibe como situada al doble de distancia que la propia imagen. Esto puede ayudar a persuadir al cerebro a adoptar la divergencia necesaria mientras se centra en la imagen cercana.

Quienes usan anteojos con lentes llamados "progresivos", en los que la distancia focal cambia gradualmente para facilitar la visión de objetos cercanos usando la parte inferior del lente, pueden descubrir que ver un estereograma es más fácil si los anteojos se empujan un poco hacia arriba para que el estereograma se vea a través de una parte del lente optimizada para imágenes que están más cerca que la distancia real al estereograma. Cuando los ojos se vuelven divergentes al mirar (o simular mirar) un objeto lejano, la sobrecorrección al mirar el estereograma a través de la parte "incorrecta" del lente puede hacer que el estereograma quede enfocado sin necesidad de superar la tendencia a enfocar el objeto lejano mientras se intenta enfocar el estereograma.
En el caso de los autoestereogramas con los ojos bizcos, es necesario adoptar un enfoque diferente. El espectador puede colocar un dedo entre los ojos y moverlo lentamente hacia la imagen, manteniendo la atención en el dedo en todo momento, hasta que esté correctamente enfocado en el punto que le permitirá ver la ilusión.
Sin embargo, no se sabe que la estereoceguera permita el uso de ninguna de estas técnicas, especialmente en personas en las que puede ser o es permanente.