Radio

Segmento en un círculo o esfera desde su centro hasta su perímetro o superficie y su longitud

Circulo con:

  circunferencia C

  diámetro D

  radio R

  centro u origen O

En geometría clásica , un radio ( pl.: radios o radios ) [ ^a] de un círculo o esfera es cualquiera de los segmentos de línea desde su centro hasta su perímetro , y en el uso más moderno, también es su longitud. El nombre proviene del latín radio , que significa rayo pero también el radio de una rueda de carro. ^[2] La abreviatura típica y el nombre de variable matemática para el radio es R o r . Por extensión, el diámetro D se define como el doble del radio: ^[3]

${\displaystyle d\doteq 2r\quad \Rightarrow \quad r={\frac {d}{2}}.}$

Si un objeto no tiene centro, el término puede referirse a su radio circunscrito , el radio de su círculo circunscrito o esfera circunscrita . En cualquier caso, el radio puede ser más de la mitad del diámetro, que suele definirse como la distancia máxima entre dos puntos cualesquiera de la figura. El radio interno de una figura geométrica suele ser el radio del círculo o esfera más grande que contiene. El radio interno de un anillo, tubo u otro objeto hueco es el radio de su cavidad.

En el caso de los polígonos regulares , el radio es igual a su circunradio. ^[4] El inradio de un polígono regular también se denomina apotema . En teoría de grafos , el radio de un grafo es el mínimo sobre todos los vértices u de la distancia máxima desde u a cualquier otro vértice del grafo. ^[5]

El radio del círculo con perímetro ( circunferencia ) C es

${\displaystyle r={\frac {C}{2\pi }}.}$

Fórmula

Para muchas figuras geométricas, el radio tiene una relación bien definida con otras medidas de la figura.

Círculos

El radio de un círculo con área A es

${\displaystyle r={\sqrt {\frac {A}{\pi }}}.}$

El radio del círculo que pasa por los tres puntos no colineales P ₁ , P ₂ y P ₃ está dado por

${\displaystyle r={\frac {|{\vec {OP_{1}}}-{\vec {OP_{3}}}|}{2\sin \theta }},}$

donde θ es el ángulo ∠ P ₁ P ₂ P ₃ . Esta fórmula utiliza la ley de los senos . Si los tres puntos se dan por sus coordenadas ( x ₁ , y ₁ ) , ( x ₂ , y ₂ ) y ( x ₃ , y ₃ ) , el radio se puede expresar como

${\displaystyle r={\frac {\sqrt {{\bigl (}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}{\bigr )}{\bigl (}(x_{2}-x_{3})^{2}+(y_{2}-y_{3})^{2}{\bigr )}{\bigl (}(x_{3}-x_{1})^{2}+(y_{3}-y_{1})^{2}{\bigr )}}}{2{\bigl |}x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3}-x_{2}y_{1}-x_{3}y_{2}{\bigr |}}}.}$

Polígonos regulares

Un cuadrado, por ejemplo ( n = 4)

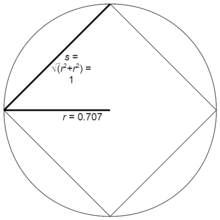
El radio r de un polígono regular con n lados de longitud s se expresa mediante r = R _n s , donde Los valores de R _n para valores pequeños de n se indican en la tabla. Si s = 1 , estos valores también son los radios de los polígonos regulares correspondientes. ${\displaystyle R_{n}=1\left/\left(2\sin {\frac {\pi }{n}}\right)\right..}$

Hipercubos

El radio de un hipercubo de dimensión d con lado s es

${\displaystyle r={\frac {s}{2}}{\sqrt {d}}.}$

Uso en sistemas de coordenadas

Coordenadas polares

El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el que cada punto de un plano está determinado por una distancia desde un punto fijo y un ángulo desde una dirección fija.

El punto fijo (análogo al origen de un sistema cartesiano ) se denomina polo , y el rayo que parte del polo en la dirección fija es el eje polar . La distancia desde el polo se denomina coordenada radial o radio , y el ángulo es la coordenada angular , ángulo polar o acimut . ^[6]

Coordenadas cilíndricas

En el sistema de coordenadas cilíndricas, hay un eje de referencia elegido y un plano de referencia elegido perpendicular a ese eje. El origen del sistema es el punto en el que las tres coordenadas pueden darse como cero. Esta es la intersección entre el plano de referencia y el eje.

El eje se denomina de diversas formas: eje cilíndrico o eje longitudinal , para diferenciarlo del eje polar , que es el rayo que se encuentra en el plano de referencia, comenzando en el origen y apuntando en la dirección de referencia.

La distancia desde el eje puede denominarse distancia radial o radio , mientras que la coordenada angular se denomina a veces posición angular o acimut . El radio y el acimut se denominan en conjunto coordenadas polares , ya que corresponden a un sistema de coordenadas polares bidimensionales en el plano que pasa por el punto, paralelo al plano de referencia. La tercera coordenada puede denominarse altura o altitud (si el plano de referencia se considera horizontal), posición longitudinal ^[7] o posición axial ^[8] .

Coordenadas esféricas

En un sistema de coordenadas esféricas, el radio describe la distancia de un punto a partir de un origen fijo. Su posición se define además mediante el ángulo polar medido entre la dirección radial y una dirección cenital fija, y el ángulo acimutal, el ángulo entre la proyección ortogonal de la dirección radial sobre un plano de referencia que pasa por el origen y es ortogonal al cenital, y una dirección de referencia fija en ese plano.

Véase también

• Radio de curvatura
• Radio de llenado en la geometría de Riemann
• Radio medio
• Radio de convergencia
• Radio de convexidad
• Radio de curvatura
• Radio de giro
• Semidiámetro

Notas

1. El plural de radio puede ser radii (del plural latino) o el plural convencional inglés radiuses . ^[1]

Referencias

1. "Radio - Definición y más del diccionario gratuito Merriam-Webster". Merriam-webster.com . Consultado el 22 de mayo de 2012 .
2. Definición de radio en dictionary.reference.com. Consultado el 8 de agosto de 2009.
3. Definición de radio en mathwords.com. Consultado el 8 de agosto de 2009.
4. Barnett Rich, Christopher Thomas (2008), Schaum's Outline of Geometry , 4.ª edición, 326 páginas. McGraw-Hill Professional. ISBN 0-07-154412-7 , ISBN 978-0-07-154412-2 . Versión en línea consultada el 8 de agosto de 2009.  
5. Jonathan L. Gross, Jay Yellen (2006), Graph theory and its applications . 2.ª edición, 779 páginas; CRC Press. ISBN 1-58488-505-X , 9781584885054. Versión en línea consultada el 8 de agosto de 2009. 
6. Brown, Richard G. (1997). Andrew M. Gleason (ed.). Matemáticas avanzadas: precálculo con matemáticas discretas y análisis de datos . Evanston, Illinois: McDougal Littell. ISBN 0-395-77114-5.
7. Krafft, C.; Volokitin, AS (1 de enero de 2002). "Resonant electron beam interaction with several lower hybrid waves". Physics of Plasmas . 9 (6): 2786–2797. Bibcode :2002PhPl....9.2786K. doi :10.1063/1.1465420. ISSN  1089-7674. Archivado desde el original el 14 de abril de 2013 . Consultado el 9 de febrero de 2013 . ...en coordenadas cilíndricas ( r , θ , z ) ... y Z=v _bz t es la posición longitudinal...
8. Groisman, Alexander; Steinberg, Victor (24 de febrero de 1997). "Pares de vórtices solitarios en flujo viscoelástico de Couette". Physical Review Letters . 78 (8). American Physical Society (APS): 1460–1463. arXiv : patt-sol/9610008 . Código Bibliográfico :1997PhRvL..78.1460G. doi :10.1103/physrevlett.78.1460. ISSN  0031-9007. S2CID  54814721. "[...]donde r , θ y z son coordenadas cilíndricas [...] en función de la posición axial[...]"