Transformación activa y pasiva

Por ejemplo, las transformaciones activas son útiles para describir las posiciones sucesivas de un cuerpo rígido.

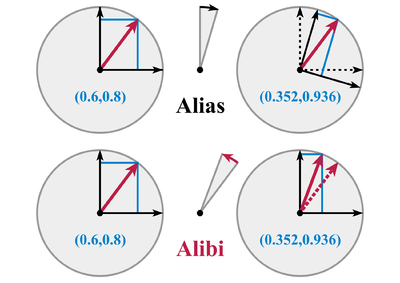
La rotación del vector a través de θ ángulo viene dada por la matriz de rotación: que se puede ver ya sea como una transformación activa o una transformación pasiva (en la que se invierte la matriz anterior), como se describe a continuación.

Para una rotación en sentido antihorario de v con respecto al sistema de coordenadas fijo: Si uno ve {R e1 , R e2 } como una nueva base, entonces las coordenadas del nuevo vector v' en la base nueva son las mismas que las de v en la base original.

Tiene sentido para escribir el nuevo vector en la base sin imprimación (como anteriormente) solo cuando la transformación es desde el espacio en sí mismo.

Para un giro hacia la izquierda de los sistemas de coordenadas: De esta ecuación se ve que las nuevas coordenadas (es decir, las coordenadas con respecto a la nueva base) son dadas por así que esto se puede escribir como Por lo tanto, para que el vector se mantenga sin cambios por la transformación pasiva, las coordenadas del vector deben transformarse de acuerdo con la inversa del operador de transformación activa.