Es el conjunto de técnicas englobadas dentro del preprocesamiento de imágenes cuyo objetivo fundamental es obtener, a partir de una imagen origen, otra final cuyo resultado sea más adecuado para una aplicación específica mejorando ciertas características de la misma que posibilite efectuar operaciones del procesado sobre ella.Los principales objetivos que se persiguen con la aplicación de filtros son: Por tanto, se consideran los filtros como operaciones que se aplican a los píxeles de una imagen digital para optimizarla, enfatizar cierta información o conseguir un efecto especial en ella.Para ello, esta se modifica siguiendo el Teorema de la Convolución correspondiente: Teorema de la Convolución (frecuencia):H(u,v): filtro atenuador de frecuencias.Como la multiplicación en el espacio de Fourier es idéntica a la convolución en el dominio espacial, todos los filtros podrían, en teoría, ser implementados como un filtro espacial.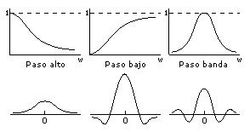Existen básicamente tres tipos distintos de filtros que pueden aplicarse: Las operaciones de filtrado se llevan a cabo directamente sobre los píxeles de la imagen.En este proceso se relaciona, para todos y cada uno de los puntos de la imagen, un conjunto de píxeles próximos al píxel objetivo con la finalidad de obtener una información útil, dependiente del tipo de filtro aplicado, que permita actuar sobre el píxel concreto en que se está llevando a cabo el proceso de filtrado para, de este modo, obtener mejoras sobre la imagen y/o datos que podrían ser utilizados en futuras acciones o procesos de trabajo sobre ella.Los filtros en el dominio del espacio pueden clasificarse en: El concepto de núcleo se entiende como una matriz de coeficientes donde el entorno del punto (x,y) que se considera en la imagen para obtener g(x,y) está determinado por el tamaño y forma del núcleo seleccionado.Dependiendo de la implementación, en los límites de la imagen se aplica un tratamiento especial (se asume un marco exterior de ceros o se repiten los valores del borde) o no se aplica ninguno.Para realizar un filtrado en el dominio del espacio se realiza una convolución (barrido) del núcleo sobre la imagen.En lo que sigue llamaremos r y s a la intensidad de los píxeles antes y después del procesado.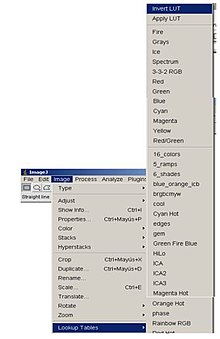Mediante ImageJ es sencillo realizar el negativo de una imagen.Esta se conseguiría a partir de la lookup table, Invert LUT.-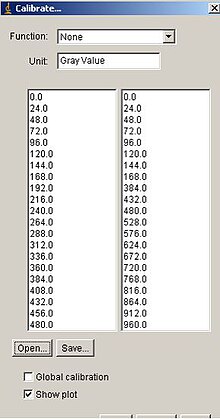Compresión del rango dinámico: Puede ocurrir que el rango dinámico de una imagen procesada excede la capacidad del dispositivo de presentación por lo que solo veremos las partes más brillantes de la imagen.En este caso se ha utilizado el Plugin "Expresion NT" , definiendo una función de la forma: s=100.log(1+| r | ) -Fraccionamiento del nivel de gris: Si se desea destacar un rango específico del nivel de gris de una imagen.se puede por ejemplo adjudicar un valor alto a todos aquellos niveles de gris del rango de interés y uno bajo a los restantes.-Fraccionamiento de los planos de bits: A veces puede desearse destacar la contribución que realizan a la imagen determinados bits específicos en vez de un rango determinado, es lo que se consigue con esta transformación.El proceso con el cual se disminuye la tasa de muestreo de una señal discreta por un factor D se denomina decimación o submuestreo (downsampling) y el proceso con el cual se aumenta la tasa de muestreo de una señal discreta por un factor T se denomina interpolación (upsampling).El orden del filtro indicará como se aproxima a través de un polinomio a la función representada por las muestras.Existen muchos filtros interpoladores y en el caso de imágenes estos se obtienen discretizando, en los valores deseados, los polinomios interpoladores.Los polinomios interpoladores utilizados frecuentemente son: líneas, cúbicos o bicúbicos.Un interpolador de orden cero básicamente efectúa un zoom duplicado.Un interpolador de orden lineal efectúa un zoom asignando el promedio de dos muestras a la muestra interpolada.A partir de los avances en la computación cuántica, ha surgido una aplicación al procesamiento digital de imágenes denominado como procesamiento cuántico de imágenes, quantum image processing en inglés y abreviado como QIMP, que aún se encuentra en etapas iniciales de investigación y cuya mayor interrogante es cómo representar una imagen digital tradicional en un computador cuántico,[1]el cual procesa la información mediante cubits de la forma:[1] De los diferentes acercamientos para representar una imagen en un computador cuántico, se encuentra FRQI (Flexible Representation for Quantum Images), que captura la posición y el color de cada pixel dentro de un estado cúantico,[2]de la forma:
Ejemplos de filtrado sobre una imagen.
Ejemplo de filtrado en el dominio de la frecuencia.
Etapas del procesamiento de imágenes en el dominio de la frecuencia.
Filtros en el dominio de la frecuencia y espacio.
Aplicación de un kernel.
Ejemplo de filtrado promedio con filtro 5x5.
Imagen original, y resultante tras filtros Laplaciano y Sobel.
