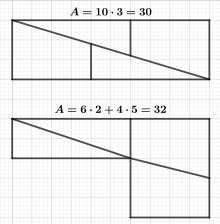
Paradoja de Hooper

Una forma geométrica con un área de 32 unidades se divide en cuatro partes, que luego se ensamblan en un rectángulo con un área de solo 30 unidades.

Esto significa que los triángulos reales de la forma original se superponen en el rectángulo.

El área superpuesta es un paralelogramo, cuyas diagonales y lados se pueden calcular mediante el teorema de Pitágoras.

William Hooper publicó la paradoja en 1774 en su libro Rational Recreations en el que lo llamó El dinero geométrico.

Sin embargo, Hooper no fue el primero en publicar esta falacia geométrica, ya que el libro de Hooper era en gran parte una adaptación del libro Nouvelles récréations physiques et mathétiques de Edmé-Gilles Guyot, que había sido publicado en Francia en 1769.