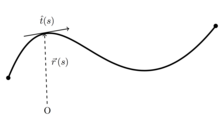
Modelo de la varilla elástica

El modelo de la varilla elástica (MVE) en la física de polímeros es usado para describir el comportamiento de los polímeros semi- flexibles; es también conocido como el modelo de Kratky-Porod, en honor a sus inventores: Otto Kratky & Günther Porod en 1949.

El MVE describe una varilla isotrópica que es continuamente flexible, esto contrasta con el Modelo de cadena libremente conectada (freely-jointed chain ) que es únicamente flexible en segmentos discretos.

El Modelo de la varilla elástica es particularmente usado para describir polímeros rígidos, con segmentos sucesivos que muestran una especie de cooperación mutua: todos apuntando en aproximadamente la misma dirección.

A temperatura ambiente, el polímero adopta una forma de conjunto suavemente curvado; a temperatura

K , el polímero adopta una forma de varilla rígida.

Para un polímero de longitud

, definimos la trayectoria del polímero como

{\displaystyle {\hat {t}}(s)}

pasa a ser el vector unitario tangencial a la cadena en

{\displaystyle {\vec {r}}(s)}

es el vector posición a lo largo de la cadena.

Entonces: Puede ocurrir que la orientación de la “función de correlación” para un modelo de varilla elástica siga un decaimiento exponencial.

es por definición la característica de persistencia del polímero.

Un valor útil es la medida del cuadrado de la distancia extremo a extremo del polímero

d s

{\displaystyle {\begin{matrix}\langle R^{2}\rangle &=&\langle {\vec {R}}\cdot {\vec {R}}\rangle \\\\\ &=&\langle \int _{0}^{l}{\hat {t}}(s)ds\cdot \int _{0}^{l}{\hat {t}}(s')ds'\rangle \\\\\ &=&\int _{0}^{l}ds\int _{0}^{l}\langle {\hat {t}}(s)\cdot {\hat {t}}(s')\rangle ds'\\\\\ &=&\int _{0}^{l}ds\int _{0}^{l}e^{-\left|s-s'\right|/P}ds'\\\\\ \langle R^{2}\rangle &=&2Pl\left[1-{\frac {P}{l}}\left(1-e^{-l/P}\right)\right]\end{matrix}}}

Varios importantes bio-polímeros pueden ser adecuadamente modelados con un Modelo de varilla elástica, por ejemplo: Instrumentos de laboratorio como el microscopio de fuerza atómica (AFM) y las pinzas ópticas son utilizados para simular la fuerza del comportamiento estirado de los polímero anteriormente mencionados.

Una fórmula de interpolación que describe el alargamiento

de un polímero MVE con perímetro de longitud

y persistencia

en reacción a una fuerza de estiramiento

es la constante de Boltzmann y

es la temperatura absoluta (Bustamante, et al., 1994; Marko et al., 1995).

En el caso particular cuando se estira el ADN en un amortiguador fisiológico (cerca del pH neutro, y fuerza iónica de aproximadamente 100mM) a temperatura ambiente el encogimiento del ADN alrededor de su perímetro está representado por, esté encogimiento entálpico, sumando una constante de estiramiento

a la ecuación anterior: Donde un valor típico para la constante de estiramiento del ADN de doble hélice es alrededor de 1000 pN y 45 nm para la persistencia(Wang, et al., 1997).