Máquina de vectores de soporte
Estos métodos están propiamente relacionados con problemas de clasificación y regresión.
Intuitivamente, una SVM es un modelo que representa a los puntos de muestra en el espacio, separando las clases a 2 espacios lo más amplios posibles mediante un hiperplano de separación definido como el vector entre los 2 puntos, de las 2 clases, más cercanos al que se llama vector soporte.
Cuando las nuevas muestras se ponen en correspondencia con dicho modelo, en función de los espacios a los que pertenezcan, pueden ser clasificadas a una o la otra clase.
De esta forma, los puntos del vector que son etiquetados con una categoría estarán a un lado del hiperplano y los casos que se encuentren en la otra categoría estarán al otro lado.
Los algoritmos SVM pertenecen a la familia de los clasificadores lineales.
En la literatura de las SVM, se llama atributo a la variable predictora y característica a un atributo transformado que es usado para definir el hiperplano.
Los modelos basados en SVM están estrechamente relacionados con las redes neuronales.
Usando una función kernel, resultan un método de formación alternativo para clasificadores polinomiales, funciones de base radial y perceptrón multicapa.
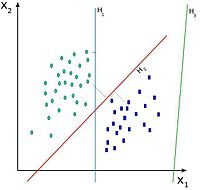
El algoritmo SVM trata de encontrar un hiperplano 1-dimensional (en el ejemplo que nos ocupa es una recta) que une a las variables predictoras y constituye el límite que define si un elemento de entrada pertenece a una categoría o a la otra.
Existe un número infinito de posibles hiperplanos (líneas) que realicen la clasificación pero, ¿cuál es la mejor y cómo la definimos?La mejor solución es aquella que permita un margen máximo entre los elementos de las dos categorías.
Se denominan vectores de soporte a los puntos que conforman las dos líneas paralelas al hiperplano, siendo la distancia entre ellas (margen) la mayor posible.
Idealmente, el modelo basado en SVM debería producir un hiperplano que separe completamente los datos del universo estudiado en dos categorías.
Con el fin de permitir cierta flexibilidad, las SVM manejan un parámetro C que controla la compensación entre errores de formación y los márgenes rígidos, creando así un margen blando (soft margin) que permita algunos errores en la clasificación a la vez que los penaliza.
Aunque es más conocida por su capacidad para separar datos en diferentes clases mediante la creación de hiperplanos, la SVM también tiene aplicaciones importantes en la regresión.
En particular, la regresión lineal basada en SVM, conocida como SVR (Support Vector Regression), se enfoca en encontrar una función que se aproxime lo mejor posible a un conjunto de datos continuos (Gema, 2022).
como el valor de salida correspondiente, se busca una función
La función buscada se puede modelar de manera lineal como:
En primer lugar, es importante mencionar que el modelo se adapta para trabajar en problemas donde la salida no es categórica, sino continua, ya que se obtendrá un número real.
Esto supone un reto para predecir la información, ya que hay una infinidad de posibilidades.
A continuación se detallan los puntos antes mencionados (Gonzalez, 2019).
Como se estudio en clase, en un problema de clasificación, el SVM busca un hiperplano que separe las clases con el máximo margen posible.
Si el error está dentro de este margen, se considera como cero.
En este enfoque, todos los puntos de datos deben caer exactamente sobre el hiperplano de regresión, sin ningún margen para el error.
Sin embargo, este enfoque es sensible a los outliers y puede resultar en un modelo que no generaliza bien a nuevos datos, ya que intenta forzar un ajuste perfecto sin flexibilidad para pequeños errores (Gema, 2022).
A diferencia del margen duro en este enfoque se permite que algunos puntos de datos caigan fuera del margen, lo que introduce una mayor flexibilidad en el modelo.
El objetivo es encontrar un equilibrio entre ajustar los datos y permitir ciertos errores, penalizando únicamente aquellos puntos que están fuera del margen 𝜖.
que controlan el error cometido por la función al aproximar un punto i-ésimo (Gema, 2022).
es una constante mayor o igual a cero que regula entre el valor de
En primer lugar, se muestra la función lagrangiana (Gema, 2022):
: Además, se deben cumplir las condiciones de KKT (Karush-Kuhn-Tucker): Estas condiciones garantizan que el punto obtenido sea una solución óptima para el problema de SVR.