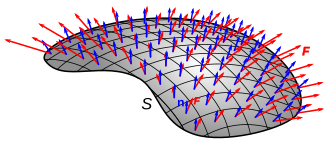
Flujo
Esto es irónico, porque Maxwell fue uno de los principales desarrolladores de los conceptos que ahora se conocen como flujo eléctrico y flujo magnético según la definición del electromagnetismo.
Esto implica que Maxwell concibió estos campos como flujos de algún tipo.
Estos identificadores se escribirán en negrita cuando y solo cuando sean vectores.
Se supone que la superficie es plana y que el flujo es constante en todas partes con respecto a la posición, y perpendicular a la superficie.
q es ahora una función de p, un punto en la superficie, y A, un área.
q es función de un punto, un área y una dirección (dada por un vector unitario
Por lo tanto, el vector unitario maximiza de forma única la función cuando apunta en la verdadera dirección del flujo.
Estas definiciones directas, especialmente la última, son bastante difíciles de manejar.
Por ejemplo, la construcción arg max es artificial desde la perspectiva de las mediciones empíricas, cuando con una veleta o similar se puede deducir fácilmente la dirección del flujo en un punto.
En lugar de definir directamente el flujo vectorial, suele ser más intuitivo enunciar algunas propiedades al respecto.
, entonces el producto escalar Es decir, la componente del flujo que pasa a través de la superficie (es decir, normal a ella) es j cos θ, mientras que la componente del flujo que pasa tangencial al área es j sin θ, pero ningún flujo realmente pasa a través del área en dirección tangencial.
A diferencia del segundo conjunto de ecuaciones, aquí la superficie no tiene por qué ser plana.
Como se mencionó anteriormente, el flujo molar químico de un componente A en un proceso isotérmico e isobárico se define en las leyes de Fick como: donde el símbolo nabla ∇ denota el operador gradiente, DAB es el coeficiente de difusión (m2·s−1) del componente A que se difunde a través del componente B, cA es la concentración (mol/m3) del componente A.
y la temperatura absoluta T por donde el segundo factor es el camino libre medio y la raíz cuadrada (con la constante de Boltzmann k) es la velocidad media de las partículas.
Para la segunda ecuación, n es la normal que apunta hacia afuera de la superficie.
Si la superficie no está cerrada, tiene como límite una curva orientada.
Se puede aplicar el flujo y estos teoremas a muchas disciplinas en las que aparecen magnitudes vectoriales (como corrientes o fuerzas) aplicadas a través de áreas.
Una "carga" eléctrica, como un solo protón en el espacio, tiene una magnitud definida en culombios.
Por lo tanto, las unidades de flujo eléctrico son, en el sistema MKS, newtons por culombio por metro cuadrado, o N m2/C.
Se utilizan dos formas de flujo eléctrico, una para el campo E:[13][14] y otra para el campo D (llamado densidad de flujo eléctrico): Esta cantidad surge en la ley de Gauss, que establece que el flujo del campo eléctrico E que sale de una superficie es proporcional a la carga eléctrica AX encerrada en la superficie (independientemente de cómo se distribuya esa carga), la forma integral es: donde ε0 es la permitividad del vacío.
Si se considera el flujo del vector de campo eléctrico, E, para un tubo cerca de una carga puntual en el campo de la carga pero que no la contiene con lados formados por líneas tangentes al campo, el flujo a través de los lados es cero, y se localiza un flujo igual y opuesto en ambos extremos del tubo.
El flujo total para cualquier superficie que rodee una carga q es q/ε0.
Aquí, la expresión "flujo de" indica una operación matemática y, como puede verse, el resultado no es necesariamente un "flujo", ya que en realidad nada fluye en las líneas de campo eléctrico.
La dirección es tal que si se permite que la corriente pase a través del cable, la fuerza electromotriz provocará una corriente que "se opone" al cambio en el campo magnético, produciendo por sí misma un campo magnético opuesto al cambio.
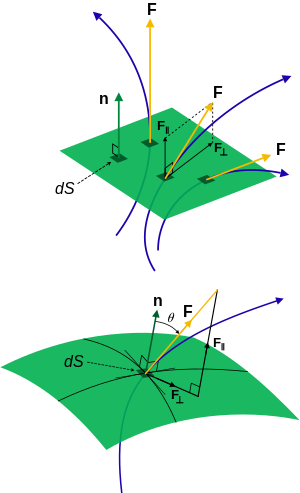
Arriba: Tres líneas de campo que pasan por una superficie plana, una normal a la superficie, una paralela y una intermedia.
Abajo: Línea de campo a través de una superficie , que muestra la configuración de la unidad normal y el elemento de superficie para calcular el flujo.