Análisis de circuitos
Existen muchas técnicas para lograrlo, Sin embargo, se asume que los componentes de los circuitos son lineales.
Los métodos descritos en este artículo solo se aplican al análisis de circuitos lineales salvo en los casos expresamente establecidos.
Para entender este artículo se necesitan saber las partes básicas de un circuito así como sus leyes fundamentales.
Una técnica particular podría reducir directamente el número de componentes, por ejemplo al combinar las resistencias en serie.
Por otro lado, se podría simplemente cambiar la forma en que está conectado un componente para posteriormente reducir el circuito de una manera más fácil.
Si las fuentes son constantes, el resultado es un circuito de corriente continua.
Se dice que dos circuitos son equivalentes respecto a una pareja de terminales cuando la tensión y la corriente que fluye a través de ellos son iguales.
Por ejemplo, los circuitos estrella y delta son circuitos de seis terminales y por lo tanto requieren tres ecuaciones simultáneas para especificar completamente su equivalencia.
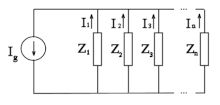
Una red general con un número arbitrario de terminales no puede reducirse al mínimo número de impedancias usando solamente combinaciones en serie o en paralelo.
Puede demostrarse que esto bastará para encontrar la red más simplificada para cualquier red arbitraria con aplicaciones sucesivas en serie, paralelo, Y-Δ y Δ-Y.
La resistencia entre cualquier nodo x e y está dada por: Para una estrella-triángulo (N=3) se reduce a: Para una reducción en serie (N=2) se reduce a: Una fuente no ideal con una impedancia interna puede representarse como una fuente de tensión ideal o una fuente de corriente ideal más la impedancia.
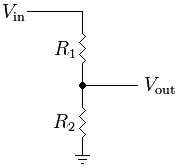
Dos o más resistencias conectadas en serie forman un divisor de tensión.
Este método funciona siempre y cuando se usen componentes lineales en el circuito.
Si el circuito es muy sencillo y solo se necesita calcular una tensión o una corriente entonces aplicando alguno de los dos métodos de redes simples podría resolverlo sin requerir a métodos más complicados.
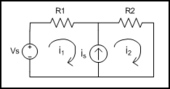
Estos circuitos se representan por un sistema algebraico de ecuaciones.
La función de transferencia Z(s) será la impedancia y tendrá unidades en ohms.
Donde A representa la atenuación, ganancia, o amplificación dependiendo del contexto.
Puede demostrarse que se requieren 4 parámetros para caracterizar completamente la red cuadripolo.
Hay muchas otras (véase el artículo principal para una lista completa), una de estas expresa todos los cuatro parámetros como impedancias.
Sin embargo, es muy raro hacerlo en la realidad debido a que en muchos casos los puertos se consideran como una entrada o una salida.
La aproximación más usada a esto es modelar la línea como una red de dos puertos y caracterizarla usando parámetros de dos puertos (o algo equivalente a esto).
Muchos de los diseños electrónicos son, en realidad, no lineales.