Árbol binario
Si algún hijo tiene como referencia a null, es decir que no almacena ningún dato, entonces este es llamado un nodo externo.
En teoría de grafos, se usa la siguiente definición: «Un árbol binario es un grafo conexo, acíclico y no dirigido tal que el grado de cada vértice no es mayor a 2».
Con la raíz escogida, cada vértice tendrá un único padre, y nunca más de dos hijos.
Existen tipos de árboles binarios que suelen usarse para fines específicos, como: Un árbol binario puede declararse de varias maneras.
Ahora pasamos a ver la implementación de los distintos recorridos: En este tipo de recorrido se realiza cierta acción (quizás simplemente imprimir por pantalla el valor de la clave de ese nodo) sobre el nodo actual y posteriormente se trata el subárbol izquierdo y cuando se haya concluido, el subárbol derecho.
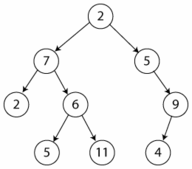
En el árbol de la figura el recorrido en preorden sería: 2, 7, 2, 6, 5, 11, 5, 9 y 4.
Implementación en pseudocódigo de forma iterativa: En este caso se trata primero el subárbol izquierdo, después el derecho y por último el nodo actual.
Esquema de implementación: En este caso el recorrido se realiza en orden por los distintos niveles del árbol.
Por ello, se debe utilizar una cola para recordar los subárboles izquierdos y derecho de cada nodo.
El esquema algoritmo para implementar un recorrido por niveles es exactamente el mismo que el utilizado en la versión iterativa del recorrido en preorden pero cambiando la estructura de datos que almacena los nodos por una cola.
Implementación en C: Para poder dibujar un árbol binario sobre la base de los recorridos, se necesitan por lo menos dos de los recorridos de profundidad (en caso de que no se repitan los nodos, ya que si se repiten los nodos es recomendable tener los tres recorridos), ya sean inorden y preorden o inorden y postorden, la única diferencia entre usar el recorrido en preorden o postorden es que en preorden se usa el primer nodo para encontrar la raíz y en postorden se usa el último nodo.
El método consiste en ir dividiendo los recorridos del árbol en pequeños subárboles, se va encontrando la raíz con el preorden o postorden y se divide en dos subárboles basándonos en el recorrido en inorden.
En el caso de que los nodos se repitan es conveniente tener los 3 recorridos para identificar más fácilmente cuál de los nodos es la raíz actual.
Para el árbol de la figura corresponden los siguientes recorridos: Preorden
Para encontrar la raíz es necesario tener el recorrido preorden o postorden, ya que la raíz es el primer nodo o el último nodo respectivamente.
Una vez encontrada la raíz, es necesario saber su posición en el recorrido inorden, del paso anterior se tiene el nodo
, pero existen 2 nodos con ese valor, el primero y el de en medio.
El recorrido inorden, es un recorrido de los árboles binarios en los que se empieza desde el nodo que se encuentra más a la izquierda de todos, sigue con la raíz y termina con los nodos del lado derecho, entonces, como en el recorrido inorden ya encontramos la raíz, la parte izquierda representa el subárbol izquierdo y la parte derecha representa el subárbol derecho.
y a la derecha se encuentran 3 valores, entonces podemos crear los recorridos para el subárbol izquierdo y el subárbol derecho Se sigue repitiendo el proceso hasta encontrar todos los nodos del árbol, en este punto la siguiente raíz izquierda es el
Cuando se llegan a nodos en los que únicamente cuentan con una rama es necesario saber que rama es la derecha y cuál es la izquierda (para algunos árboles con balanceo como los AVL), por ejemplo siguiendo la rama de la derecha partiendo de que el
Finalmente el siguiente nodo se coloca a la izquierda del
En la figura adjunta se puede observar la estructura de dicha implementación.
(partiendo de que la raíz tenga índice cero).
Este método tiene como ventajas el tener almacenados los datos de forma más compacta y por tener una forma más rápida y eficiente de localizar los datos en particular durante un preoden transversal.
Por ejemplo, en el árbol de la izquierda, la A tiene 6 hijos (B, C, D, E, F, G).
El árbol binario puede ser pensado como el árbol original inclinado hacia los lados, con los bordes negros izquierdos representando el primer hijo y los azules representado los siguientes hermanos.