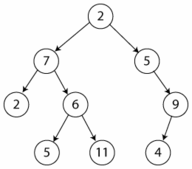
Un árbol que no está vacío consta de un nodo raíz y potencialmente muchos niveles de nodos adicionales que forman una jerarquía.Para permitir que los árboles puedan ser finitos, hay que, o bien permitir que la lista de los hijos pueda estar vacía, o permitir que los árboles puedan estar vacíos, en cuyo caso la lista de los hijos pueden ser de tamaño fijo (factor de ramificación, especialmente 2 o binario), si se desea.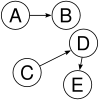Esta estructura de datos realmente define a un grafo dirigido,[1] porque puede tener bucles o varias referencias al mismo nodo, del mismo modo que una lista enlazada.Esta estructura de datos define un grafo dirigido,[1] y para que sea un árbol hay que añadir una condición en su estructura global (en su topología), y esto es que a lo sumo una referencia puede apuntar a cualquier nodo dado (un nodo tiene como máximo un solo padre), y ningún nodo del árbol puede apuntar a la raíz.De hecho, todos los nodos (que no sean la raíz) deben tener exactamente un padre, y la raíz no debe tener ningún padre.Un nodo es una estructura que puede contener un valor o condición, o representar una estructura de datos separada (que puede llegar a ser un árbol).Dependiendo de la definición, un árbol puede ser obligado a tener un nodo raíz (en cuyo caso ningún árbol estaría vacío), o que se les permita estar vacíos, en cuyo caso no necesariamente tienen un nodo raíz.Tenga en cuenta que algunos algoritmos comienzan en la raíz, pero primero visitan a los nodos hoja (acceden al valor de los nodos hoja), y acceden por último a la raíz (es decir, que acceden por primera vez a los hijos de la raíz, pero solo acceder al valor de la raíz como último paso).Todos los demás nodos pueden ser accedidos siguiendo los brazos o enlaces.En los diagramas, el nodo raíz se extrae convencionalmente en la parte superior.Los árboles ordenados pueden ser representados esencial y únicamente en el plano, y están por lo tanto llamados árboles de plano, de la siguiente manera: si uno fija un orden convencional (por ejemplo, en el sentido de las agujas del reloj), y dispone a los nodos secundarios en ese orden (primer brazo entrante de un padre, a continuación, primer brazo de hijo, etc.), esto produce una incrustación del árbol en el plano.A la inversa, tal incrustación determina un orden de los nodos secundarios.En general un nodo en un árbol no tendrá punteros a sus padres, pero esta información puede ser incluida (ampliando la estructura de datos para incluir también un puntero al vector) o almacenarse por separado.Alternativamente, los enlaces ascendentes pueden ser incluidos en los datos del nodo hijo, como en un árbol binario enlazado.Los brazos se consideran todavía como pares de nodos, sin embargo, los términos padres e hijos generalmente se sustituyen por terminología diferente (por ejemplo, fuente y objetivo).
Un árbol simple sin ordenar. En este diagrama, el nodo con la etiqueta 7 tiene dos hijos, el 2 y el 6, y un padre, el 2. La raíz, al inicio, no tiene padre.
No es un árbol: Hay dos partes sin
conectar
(A→B y C→D→E), luego existe más de una raíz.
No es un árbol: En el ciclo 1-2-4-3, el 4 tiene más de un padre.
No es un árbol: En el ciclo B→C→E→D→B, B tiene más de un padre.
No es un árbol: En el ciclo A→A, A es la raíz, pero también tiene un padre.
Cada lista lineal es trivialmente un árbol
Las rotaciones en árboles binarios son operaciones internas comunes utilizadas para mantener el balance perfecto (o casi perfecto) del árbol binario. Un árbol balanceado permite operaciones en tiempo logarítmico.
