
/r[aeiou]+/gUna expresión regular (abreviada como regex o regexp ), [1] a veces denominada expresión racional , [2] [3] es una secuencia de caracteres que especifica un patrón de coincidencia en un texto . Por lo general, estos patrones son utilizados por algoritmos de búsqueda de cadenas para operaciones de "buscar" o "buscar y reemplazar" en cadenas , o para la validación de entradas . Las técnicas de expresión regular se desarrollan en la ciencia informática teórica y la teoría del lenguaje formal .
El concepto de expresiones regulares comenzó en la década de 1950, cuando el matemático estadounidense Stephen Cole Kleene formalizó el concepto de lenguaje regular . Su uso se generalizó con las utilidades de procesamiento de texto de Unix . Desde la década de 1980 existen distintas sintaxis para escribir expresiones regulares, una de ellas es el estándar POSIX y otra, ampliamente utilizada, es la sintaxis de Perl .
Las expresiones regulares se utilizan en motores de búsqueda , en cuadros de diálogo de búsqueda y reemplazo de procesadores de texto y editores de texto , en utilidades de procesamiento de texto como sed y AWK , y en análisis léxico . Las expresiones regulares son compatibles con muchos lenguajes de programación. Las implementaciones de bibliotecas a menudo se denominan " motores ", [4] [5] y muchas de ellas están disponibles para su reutilización.

Las expresiones regulares se originaron en 1951, cuando el matemático Stephen Cole Kleene describió los lenguajes regulares utilizando su notación matemática llamada eventos regulares . [6] [7] Estas surgieron en la informática teórica , en los subcampos de la teoría de autómatas (modelos de computación) y la descripción y clasificación de lenguajes formales , motivadas por el intento de Kleene de describir las primeras redes neuronales artificiales . (Kleene lo introdujo como una alternativa al "prehensible" de McCulloch & Pitts , pero admitió que "daríamos la bienvenida a cualquier sugerencia sobre un término más descriptivo". [8] ) Otras implementaciones tempranas de coincidencia de patrones incluyen el lenguaje SNOBOL , que no usaba expresiones regulares, sino sus propias construcciones de coincidencia de patrones.
Las expresiones regulares entraron en uso popular a partir de 1968 en dos usos: coincidencia de patrones en un editor de texto [9] y análisis léxico en un compilador. [10] Una de las primeras apariciones de expresiones regulares en forma de programa fue cuando Ken Thompson construyó la notación de Kleene en el editor QED como un medio para hacer coincidir patrones en archivos de texto . [9] [11] [12] [13] Para mayor velocidad, Thompson implementó la coincidencia de expresiones regulares mediante compilación justo a tiempo (JIT) en código IBM 7094 en el Sistema de tiempo compartido compatible , un importante ejemplo temprano de compilación JIT. [14] Más tarde agregó esta capacidad al editor de Unix ed , lo que eventualmente llevó al uso de expresiones regulares por parte de la popular herramienta de búsqueda grep ("grep" es una palabra derivada del comando para la búsqueda de expresiones regulares en el editor ed: que significa "Búsqueda global de líneas coincidentes de Expresión regular e Impresión"). [15] Casi al mismo tiempo en que Thompson desarrolló QED, un grupo de investigadores, entre ellos Douglas T. Ross, implementaron una herramienta basada en expresiones regulares que se utiliza para el análisis léxico en el diseño de compiladores . [10]g/re/p
En los años 70, se utilizaron muchas variaciones de estas formas originales de expresiones regulares en programas Unix [13] de los Laboratorios Bell , incluidos lex , sed , AWK y expr , y en otros programas como vi y Emacs (que tiene su propia sintaxis y comportamiento incompatibles). Posteriormente, una amplia gama de programas adoptaron expresiones regulares, y estas primeras formas se estandarizaron en el estándar POSIX.2 en 1992.
En la década de 1980, surgieron las expresiones regulares más complicadas en Perl , que originalmente derivaron de una biblioteca de expresiones regulares escrita por Henry Spencer (1986), quien más tarde escribió una implementación para Tcl llamada Advanced Regular Expressions . [16] La biblioteca Tcl es una implementación híbrida NFA / DFA con características de rendimiento mejoradas. Los proyectos de software que han adoptado la implementación de expresiones regulares Tcl de Spencer incluyen PostgreSQL . [17] Perl luego amplió la biblioteca original de Spencer para agregar muchas características nuevas. [18] Parte del esfuerzo en el diseño de Raku (anteriormente llamado Perl 6) es mejorar la integración de expresiones regulares de Perl y aumentar su alcance y capacidades para permitir la definición de gramáticas de expresiones de análisis . [19] El resultado es un minilenguaje llamado reglas de Raku , que se utilizan para definir la gramática de Raku y también para proporcionar una herramienta a los programadores en el lenguaje. Estas reglas mantienen características existentes de las expresiones regulares de Perl 5.x, pero también permiten la definición al estilo BNF de un analizador descendente recursivo a través de subreglas.
El uso de expresiones regulares en los estándares de información estructurada para el modelado de documentos y bases de datos comenzó en la década de 1960 y se expandió en la década de 1980 cuando se consolidaron estándares de la industria como ISO SGML (precursorizado por ANSI "GCA 101-1983"). El núcleo de los estándares de lenguaje de especificación de estructuras consiste en expresiones regulares. Su uso es evidente en la sintaxis del grupo de elementos DTD . Antes del uso de expresiones regulares, muchos lenguajes de búsqueda permitían comodines simples, por ejemplo "*" para coincidir con cualquier secuencia de caracteres y "?" para coincidir con un solo carácter. Hoy en día se pueden encontrar reliquias de esto en la sintaxis glob para nombres de archivos y en el operador SQL LIKE .
A partir de 1997, Philip Hazel desarrolló PCRE (Perl Compatible Regular Expressions), que intenta imitar de cerca la funcionalidad de expresiones regulares de Perl y es utilizado por muchas herramientas modernas, incluyendo PHP y Apache HTTP Server . [20]
Hoy en día, las expresiones regulares son ampliamente compatibles en lenguajes de programación, programas de procesamiento de texto (en particular, analizadores léxicos ), editores de texto avanzados y algunos otros programas. La compatibilidad con expresiones regulares es parte de la biblioteca estándar de muchos lenguajes de programación, incluidos Java y Python , y está integrada en la sintaxis de otros, incluidos Perl y ECMAScript . A fines de la década de 2010, varias empresas comenzaron a ofrecer implementaciones de hardware, FPGA [21] , GPU [22] de motores de expresiones regulares compatibles con PCRE que son más rápidos en comparación con las implementaciones de CPU .
La frase expresiones regulares , o regexes , se utiliza a menudo para referirse a la sintaxis textual estándar y específica para representar patrones para la coincidencia de texto, a diferencia de la notación matemática que se describe a continuación. Cada carácter de una expresión regular (es decir, cada carácter de la cadena que describe su patrón) es un metacarácter , que tiene un significado especial, o un carácter regular que tiene un significado literal. Por ejemplo, en la expresión regular b., 'b' es un carácter literal que coincide solo con 'b', mientras que '.' es un metacarácter que coincide con todos los caracteres excepto una nueva línea. Por lo tanto, esta expresión regular coincide, por ejemplo, con 'b%', 'bx' o 'b5'. Juntos, los metacaracteres y los caracteres literales se pueden utilizar para identificar texto de un patrón determinado o procesar una cantidad de instancias del mismo. Las coincidencias de patrones pueden variar desde una igualdad precisa hasta una similitud muy general, según lo controlen los metacaracteres. Por ejemplo, .es un patrón muy general [a-z](coincide con todas las letras minúsculas de la 'a' a la 'z') es menos general y bes un patrón preciso (coincide solo con la 'b'). La sintaxis de metacaracteres está diseñada específicamente para representar objetivos prescritos de una manera concisa y flexible para dirigir la automatización del procesamiento de texto de una variedad de datos de entrada, en una forma fácil de escribir usando un teclado ASCII estándar .
Un caso muy simple de una expresión regular en esta sintaxis es localizar una palabra escrita de dos formas diferentes en un editor de texto ; la expresión regular seriali[sz]ecoincide con "serialise" y "serialize". Los caracteres comodín también logran esto, pero están más limitados en lo que pueden modelar, ya que tienen menos metacaracteres y una base de lenguaje simple.
El contexto habitual de los caracteres comodín es la inclusión de nombres similares en una lista de archivos, mientras que las expresiones regulares se emplean normalmente en aplicaciones que buscan coincidencias de patrones en cadenas de texto en general. Por ejemplo, la expresión regular busca coincidencias de espacios en blanco en exceso al principio o al final de una línea. Una expresión regular avanzada que busca coincidencias con cualquier número es .^[ \t]+|[ \t]+$[+-]?(\d+(\.\d*)?|\.\d+)([eE][+-]?\d+)?

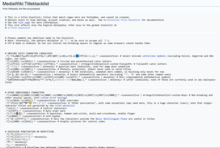
Un procesador de expresiones regulares traduce una expresión regular en la sintaxis anterior en una representación interna que se puede ejecutar y comparar con una cadena que representa el texto que se busca. Un enfoque posible es el algoritmo de construcción de Thompson para construir un autómata finito no determinista (NFA), que luego se vuelve determinista y el autómata finito determinista (DFA) resultante se ejecuta en la cadena de texto de destino para reconocer subcadenas que coinciden con la expresión regular. La imagen muestra el esquema NFA obtenido a partir de la expresión regular , donde s denota a su vez una expresión regular más simple, que ya se ha traducido recursivamente al NFA N ( s ).N(s*)s*
Una expresión regular, a menudo llamada patrón , especifica un conjunto de cadenas necesarias para un propósito particular. Una forma sencilla de especificar un conjunto finito de cadenas es enumerar sus elementos o miembros. Sin embargo, a menudo hay formas más concisas: por ejemplo, el conjunto que contiene las tres cadenas "Handel", "Händel" y "Haendel" se puede especificar mediante el patrón H(ä|ae?)ndel; decimos que este patrón coincide con cada una de las tres cadenas. Sin embargo, puede haber muchas formas de escribir una expresión regular para el mismo conjunto de cadenas: por ejemplo, (Hän|Han|Haen)deltambién especifica el mismo conjunto de tres cadenas en este ejemplo.
La mayoría de los formalismos proporcionan las siguientes operaciones para construir expresiones regulares.
gray|greygray|greyy son patrones equivalentes que describen el conjunto de "gris" o "gris".gr(a|e)y? , el asterisco * (derivado de la estrella de Kleene ) y el signo más + ( más de Kleene )..coincide con cualquier carácter. Por ejemplo,a.bcoincide con cualquier cadena que contenga una "a", luego cualquier carácter y luego "b".a.*bcoincide con cualquier cadena que contenga una "a" y luego el carácter "b" en algún punto posterior.Estas construcciones se pueden combinar para formar expresiones arbitrariamente complejas, de forma similar a como se pueden construir expresiones aritméticas a partir de números y las operaciones +, −, × y ÷.
La sintaxis precisa de las expresiones regulares varía según las herramientas y el contexto; se brindan más detalles en § Sintaxis.
Las expresiones regulares describen los lenguajes regulares en la teoría del lenguaje formal . Tienen el mismo poder expresivo que las gramáticas regulares .
Las expresiones regulares constan de constantes, que denotan conjuntos de cadenas, y símbolos operadores, que denotan operaciones sobre estos conjuntos. La siguiente definición es estándar y se encuentra como tal en la mayoría de los libros de texto sobre teoría del lenguaje formal. [24] [25] Dado un alfabeto finito Σ, las siguientes constantes se definen como expresiones regulares:
aen Σ que denota el conjunto que contiene solo el carácter a .Dadas las expresiones regulares R y S, se definen las siguientes operaciones sobre ellas para producir expresiones regulares:
(RS)denota el conjunto de cadenas que se pueden obtener concatenando una cadena aceptada por R y una cadena aceptada por S (en ese orden). Por ejemplo, sea R {"ab", "c"} y S {"d", "ef"}. Entonces, denota (RS){"abd", "abef", "cd", "cef"}.(R|S)denota la unión de conjuntos descritos por R y S. Por ejemplo, si R describe {"ab", "c"} y S describe {"ab", "d", "ef"}, expresión (R|S)describe {"ab", "c", "d", "ef"}.(R*)denota el superconjunto más pequeño del conjunto descrito por R que contiene ε y está cerrado bajo concatenación de cadenas. Este es el conjunto de todas las cadenas que se pueden formar concatenando cualquier número finito (incluido cero) de cadenas del conjunto descrito por R. Por ejemplo, si R denota {"0", "1"}, (R*)denota el conjunto de todas las cadenas binarias finitas (incluida la cadena vacía). Si R denota {"ab", "c"}, (R*)denota {ε, "ab", "c", "abab", "abc", "cab", "cc", "ababab", "abcab", ...}.Para evitar los paréntesis, se supone que la estrella de Kleene tiene la máxima prioridad, seguida de la concatenación y luego la alternancia. Si no hay ninguna ambigüedad, se pueden omitir los paréntesis. Por ejemplo, (ab)cse puede escribir como abc, y a|(b(c*))se puede escribir como a|bc*. Muchos libros de texto utilizan los símbolos ∪, + o ∨ para la alternancia en lugar de la barra vertical.
Ejemplos:
a|b*denota {ε, "a", "b", "bb", "bbb", ...}(a|b)*denota el conjunto de todas las cadenas sin símbolos distintos de "a" y "b", incluida la cadena vacía: {ε, "a", "b", "aa", "ab", "ba", "bb", "aaa", ...}ab*(c|ε)denota el conjunto de cadenas que comienzan con "a", luego cero o más "b" y finalmente, opcionalmente, una "c": {"a", "ac", "ab", "abc", "abb", "abbc", ...}(0|(1(01*0)*1))*denota el conjunto de números binarios que son múltiplos de 3: { ε, "0", "00", "11", "000", "011", "110", "0000", "0011", "0110", "1001", "1100", "1111", "00000", ... }La definición formal de expresiones regulares es mínima a propósito, y evita definir ?y +; se pueden expresar de la siguiente manera: a+= aa*, y a?= . A veces se agrega (a|ε)el operador de complemento para dar una expresión regular generalizada ; aquí R c coincide con todas las cadenas sobre Σ* que no coinciden con R . En principio, el operador de complemento es redundante, porque no otorga más poder expresivo. Sin embargo, puede hacer que una expresión regular sea mucho más concisa: eliminar un solo operador de complemento puede causar una explosión exponencial doble de su longitud. [26] [27] [28]
Las expresiones regulares en este sentido pueden expresar los lenguajes regulares, exactamente la clase de lenguajes aceptados por los autómatas finitos deterministas . Sin embargo, hay una diferencia significativa en compacidad. Algunas clases de lenguajes regulares solo pueden describirse mediante autómatas finitos deterministas cuyo tamaño crece exponencialmente en el tamaño de las expresiones regulares equivalentes más cortas. El ejemplo estándar aquí son los lenguajes L k que consisten en todas las cadenas sobre el alfabeto { a , b } cuya k ésima-desde-la-última letra es igual a . Por un lado, una expresión regular que describe L 4 está dada por .
Generalizando este patrón a L k obtenemos la expresión:
Por otra parte, se sabe que todo autómata finito determinista que acepte el lenguaje L k debe tener al menos 2 k estados. Afortunadamente, existe una aplicación sencilla de las expresiones regulares a los autómatas finitos no deterministas (AFN) más generales que no conduce a tal explosión en tamaño; por esta razón, los AFN se utilizan a menudo como representaciones alternativas de los lenguajes regulares. Los AFN son una variación simple de las gramáticas de tipo 3 de la jerarquía de Chomsky . [24]
En la dirección opuesta, hay muchos idiomas que se describen fácilmente con un DFA pero que no se describen fácilmente con una expresión regular. Por ejemplo, determinar la validez de un ISBN dado requiere calcular el módulo del entero base 11, y se puede implementar fácilmente con un DFA de 11 estados. Sin embargo, convertirlo a una expresión regular da como resultado un archivo de 2,14 megabytes. [29]
Dada una expresión regular, el algoritmo de construcción de Thompson calcula un autómata finito no determinista equivalente. Una conversión en la dirección opuesta se logra mediante el algoritmo de Kleene .
Por último, cabe señalar que muchos motores de "expresiones regulares" del mundo real implementan características que no se pueden describir mediante expresiones regulares en el sentido de la teoría del lenguaje formal; en lugar de eso, implementan expresiones regulares . Vea a continuación para obtener más información sobre esto.
Como se ve en muchos de los ejemplos anteriores, hay más de una forma de construir una expresión regular para lograr los mismos resultados.
Es posible escribir un algoritmo que, para dos expresiones regulares dadas, decida si los lenguajes descritos son iguales; el algoritmo reduce cada expresión a una máquina de estados finitos determinista mínima y determina si son isomorfas (equivalentes).
Las leyes algebraicas para expresiones regulares se pueden obtener utilizando un método de Gischer que se explica mejor con un ejemplo: Para comprobar si ( X + Y ) * y ( X * Y * ) * denotan el mismo lenguaje regular, para todas las expresiones regulares X , Y , es necesario y suficiente comprobar si las expresiones regulares particulares ( a + b ) * y ( a * b * ) * denotan el mismo lenguaje sobre el alfabeto Σ={ a , b }. De manera más general, una ecuación E = F entre términos de expresión regular con variables se cumple si, y solo si, se cumple su instanciación con diferentes variables reemplazadas por diferentes constantes de símbolo. [30] [31]
Toda expresión regular puede escribirse únicamente en términos de la estrella de Kleene y uniones de conjuntos sobre palabras finitas. Este es un problema sorprendentemente difícil. Tan simples como son las expresiones regulares, no hay un método para reescribirlas sistemáticamente a alguna forma normal. La falta de axioma en el pasado condujo al problema de la altura de la estrella . En 1991, Dexter Kozen axiomatizó las expresiones regulares como un álgebra de Kleene , utilizando axiomas ecuacionales y de cláusula de Horn . [32] Ya en 1964, Redko había demostrado que ningún conjunto finito de axiomas puramente ecuacionales puede caracterizar el álgebra de los lenguajes regulares. [33]
Un patrón de expresión regular coincide con una cadena de destino . El patrón está compuesto por una secuencia de átomos . Un átomo es un único punto dentro del patrón de expresión regular que intenta hacer coincidir con la cadena de destino. El átomo más simple es un literal, pero agrupar partes del patrón para que coincida con un átomo requerirá el uso ( )de metacaracteres. Los metacaracteres ayudan a formar: átomos ; cuantificadores que indican cuántos átomos (y si es un cuantificador voraz o no); un carácter lógico OR, que ofrece un conjunto de alternativas, y un carácter lógico NOT, que niega la existencia de un átomo; y referencias hacia atrás para hacer referencia a átomos anteriores de un patrón de átomos que se completa. Se realiza una coincidencia, no cuando coinciden todos los átomos de la cadena, sino cuando todos los átomos del patrón en la expresión regular han coincidido. La idea es hacer que un pequeño patrón de caracteres represente una gran cantidad de cadenas posibles, en lugar de compilar una gran lista de todas las posibilidades literales.
Dependiendo del procesador de expresiones regulares, hay alrededor de catorce metacaracteres, caracteres que pueden tener o no su significado literal , dependiendo del contexto, o si están "escapados", es decir, precedidos por una secuencia de escape , en este caso, la barra invertida \. Las expresiones regulares modernas y extendidas de POSIX usan metacaracteres con más frecuencia que su significado literal, por lo que para evitar la "barra invertida-osis" o el síndrome del palillo de dientes inclinado , tienen un escape de metacaracteres a un modo literal; sin embargo, al principio tienen los cuatro metacaracteres entre corchetes ( )y { }ser principalmente literales, y "escapan" este significado habitual para convertirse en metacaracteres. Los estándares comunes implementan ambos. Los metacaracteres habituales son {}[]()^$.|*+?y \. Los caracteres habituales que se convierten en metacaracteres cuando se escapan son dswDSWy N.
Al ingresar una expresión regular en un lenguaje de programación, se puede representar como una cadena literal habitual, por lo tanto, generalmente entre comillas; esto es común en C, Java y Python, por ejemplo, donde la expresión regular rese ingresa como "re". Sin embargo, a menudo se escriben con barras como delimitadores , como en /re/para la expresión regular re. Esto se origina en ed , donde es el comando del editor para buscar, y se puede usar /una expresión para especificar un rango de líneas (que coincidan con el patrón), que se puede combinar con otros comandos en ambos lados, el más famoso como en grep ("impresión de expresión regular global"), que se incluye en la mayoría de los sistemas operativos basados en Unix , como las distribuciones de Linux . Una convención similar se usa en sed , donde la búsqueda y el reemplazo se dan por y los patrones se pueden unir con una coma para especificar un rango de líneas como en . Esta notación es particularmente conocida debido a su uso en Perl , donde forma parte de la sintaxis distinta de los literales de cadena normales. En algunos casos, como en sed y Perl, se pueden utilizar delimitadores alternativos para evitar colisiones con el contenido y para evitar tener que escapar las apariciones del carácter delimitador en el contenido. Por ejemplo, en sed, el comando reemplazará a por an , utilizando comas como delimitadores./re/g/re/ps/re/replacement//re1/,/re2/s,/,X,/X
El estándar IEEE POSIX tiene tres conjuntos de compatibilidad: BRE (expresiones regulares básicas), [34] ERE (expresiones regulares extendidas) y SRE (expresiones regulares simples). SRE está en desuso [35] en favor de BRE, ya que ambos brindan compatibilidad con versiones anteriores . La subsección a continuación que cubre las clases de caracteres se aplica tanto a BRE como a ERE.
BRE y ERE trabajan juntos. ERE agrega ?, +, y |, y elimina la necesidad de escapar los metacaracteres ( )y { }, que son necesarios en BRE. Además, siempre que se respete la sintaxis estándar POSIX para expresiones regulares, puede haber, y a menudo hay, sintaxis adicional para servir a aplicaciones específicas (pero compatibles con POSIX). Aunque POSIX.2 deja sin definir algunos detalles de implementación, BRE y ERE proporcionan un "estándar" que desde entonces se ha adoptado como la sintaxis predeterminada de muchas herramientas, donde la elección de los modos BRE o ERE suele ser una opción admitida. Por ejemplo, GNU grep tiene las siguientes opciones: " grep -E" para ERE, y " grep -G" para BRE (el valor predeterminado), y " grep -P" para expresiones regulares de Perl .
Las expresiones regulares de Perl se han convertido en un estándar de facto, con un conjunto rico y poderoso de expresiones atómicas. Perl no tiene niveles "básicos" o "extendidos". Al igual que en los ERE de POSIX, ( )se { }tratan como metacaracteres a menos que se escapen; se sabe que otros metacaracteres son literales o simbólicos según el contexto únicamente. La funcionalidad adicional incluye coincidencia diferida, referencias inversas, grupos de captura con nombre y patrones recursivos .
En el estándar POSIX , la sintaxis regular básica ( BRE ) requiere que los metacaracteres ( ) y { }se designen como \(\)y \{\}, mientras que la sintaxis regular extendida ( ERE ) no lo requiere.
Ejemplos:
.atcoincide con cualquier cadena de tres caracteres que termine en "at", incluidos "hat", "cat", "bat", "4at", "#at" y "at" (que comienzan con un espacio).[hc]atcoincide con "sombrero" y "gato".[^b]atcoincide con todas las cadenas coincidentes con .atexcepto "bat".[^hc]atcoincide con todas las cadenas que coinciden con .atotras que no sean "hat" y "cat".^[hc]atcoincide con "sombrero" y "gato", pero sólo al principio de la cadena o línea.[hc]at$coincide con "sombrero" y "gato", pero sólo al final de la cadena o línea.\[.\]coincide con cualquier carácter individual rodeado por "[" y "]" ya que los corchetes se escapan, por ejemplo: "[a]", "[b]", "[7]", "[@]", "[]]" y "[ ]" (corchete de espacio entre corchetes).s.*coincide con s seguido de cero o más caracteres, por ejemplo: "s", "saw", "seed", "s3w96.7" y "s6#h%(>>>mn mQ".Según Ross Cox, la especificación POSIX requiere que las subexpresiones ambiguas se gestionen de una manera diferente a la de Perl. El comité reemplazó las reglas de Perl por otras que son fáciles de explicar, pero las nuevas reglas "simples" son en realidad más complejas de implementar: eran incompatibles con las herramientas preexistentes y hacían que fuera esencialmente imposible definir una extensión de "coincidencia diferida" (ver más abajo). Como resultado, muy pocos programas implementan realmente las reglas de subexpresiones POSIX (incluso cuando implementan otras partes de la sintaxis POSIX). [37]
El significado de los metacaracteres que se escapan con una barra invertida se invierte para algunos caracteres en la sintaxis de expresiones regulares extendidas ( ERE ) de POSIX. Con esta sintaxis, una barra invertida hace que el metacarácter se trate como un carácter literal. Por ejemplo, \( \)is now ( )y \{ \}is now { }. Además, se elimina la compatibilidad con referencias inversas y se agregan los siguientes metacaracteres:\n
Ejemplos:
[hc]?atcoincide con "at", "hat" y "cat".[hc]*atcoincide con "at", "hat", "cat", "hhat", "chat", "hcat", "cchchat", etc.[hc]+atcoincide con "hat", "cat", "hhat", "chat", "hcat", "cchchat", etc., pero no con "at".cat|dogcoincide con "gato" o "perro".Las expresiones regulares extendidas POSIX a menudo se pueden usar con utilidades Unix modernas incluyendo el indicador de línea de comando -E .
La clase de caracteres es el concepto de expresión regular más básico después de una coincidencia literal. Hace que una pequeña secuencia de caracteres coincida con un conjunto más grande de caracteres. Por ejemplo, [A-Z]podría representar cualquier letra mayúscula del alfabeto inglés y podría significar cualquier dígito. Las clases de caracteres se aplican a ambos niveles de POSIX.\d
Al especificar un rango de caracteres, como [a-Z](es decir, de minúsculas aa mayúsculas Z), la configuración regional de la computadora determina el contenido según el orden numérico de la codificación de caracteres. Pueden almacenar dígitos en esa secuencia, o el orden puede ser abc...zABC...Z o aAbBcC...zZ . Por lo tanto, el estándar POSIX define una clase de caracteres, que será conocida por el procesador de expresiones regulares instalado. Esas definiciones se encuentran en la siguiente tabla:
Las clases de caracteres POSIX solo se pueden utilizar dentro de expresiones entre corchetes. Por ejemplo, coincide con las letras mayúsculas y minúsculas "a" y "b".[[:upper:]ab]
Una clase no POSIX adicional que entienden algunas herramientas es [:word:], que suele definirse como [:alnum:]más guión bajo. Esto refleja el hecho de que en muchos lenguajes de programación estos son los caracteres que se pueden utilizar en los identificadores. El editor Vim distingue además las clases de palabras y de encabezado de palabra (utilizando la notación y ) ya que en muchos lenguajes de programación los caracteres que pueden comenzar un identificador no son los mismos que pueden aparecer en otras posiciones: los números suelen excluirse, por lo que un identificador se vería como o en notación POSIX.\w\h\h\w*[[:alpha:]_][[:alnum:]_]*
Tenga en cuenta que lo que los estándares de expresiones regulares POSIX denominan clases de caracteres se conoce comúnmente como clases de caracteres POSIX en otros tipos de expresiones regulares que las admiten. En la mayoría de los otros tipos de expresiones regulares, el término clase de caracteres se utiliza para describir lo que POSIX denomina expresiones entre corchetes .
Debido a su poder expresivo y (relativa) facilidad de lectura, muchas otras utilidades y lenguajes de programación han adoptado una sintaxis similar a la de Perl , por ejemplo, Java , JavaScript , Julia , Python , Ruby , Qt , .NET Framework de Microsoft y XML Schema . Algunos lenguajes y herramientas como Boost y PHP admiten múltiples variantes de expresiones regulares. Las implementaciones de expresiones regulares derivadas de Perl no son idénticas y generalmente implementan un subconjunto de características que se encuentran en Perl 5.0, lanzado en 1994. Perl a veces incorpora características que inicialmente se encontraban en otros lenguajes. Por ejemplo, Perl 5.10 implementa extensiones sintácticas desarrolladas originalmente en PCRE y Python. [38]
En Python y algunas otras implementaciones (por ejemplo, Java), los tres cuantificadores comunes ( *, +y ?) son codiciosos de manera predeterminada porque coinciden con tantos caracteres como sea posible. [39] La expresión regular ".+"(incluidas las comillas dobles) aplicada a la cadena
"Ganímedes", continuó, "es la luna más grande del Sistema Solar".
coincide con toda la línea (porque toda la línea comienza y termina con comillas dobles) en lugar de coincidir solo con la primera parte. "Ganymede,"Sin embargo, los cuantificadores antes mencionados pueden hacerse perezosos o mínimos o reacios , haciendo coincidir la menor cantidad de caracteres posible, agregando un signo de interrogación: ".+?"coincide solo con "Ganymede,". [39]
En Java y Python 3.11+, [40] los cuantificadores pueden volverse posesivos agregando un signo más, lo que deshabilita el retroceso (en un motor de retroceso), incluso si al hacerlo se permitiría que la coincidencia general tenga éxito: [41] Mientras que la expresión regular ".*"aplicada a la cadena
"Ganímedes", continuó, "es la luna más grande del Sistema Solar".
coincide con toda la línea, la expresión regular ".*+"no coincide en absoluto , porque .*+consume toda la entrada, incluido el final ". Por lo tanto, los cuantificadores posesivos son más útiles con clases de caracteres negados, por ejemplo "[^"]*+", que coincide "Ganymede,"cuando se aplica a la misma cadena.
Otra extensión común que cumple la misma función es la agrupación atómica, que desactiva el retroceso para un grupo entre paréntesis. La sintaxis típica es (?>group) . Por ejemplo, mientras que ^(wi|w)i$ coincide con wi y wii , ^(?>wi|w)i$ solo coincide con wii porque el motor tiene prohibido el retroceso y, por lo tanto, no puede intentar configurar el grupo como "w" después de coincidir con "wi". [42]
Los cuantificadores posesivos son más fáciles de implementar que los cuantificadores codiciosos y perezosos, y suelen ser más eficientes en tiempo de ejecución. [41]
La RFC 9485 de IETF describe "I-Regexp: un formato de expresión regular interoperable". Especifica un subconjunto limitado de expresiones regulares diseñadas para ser interoperables, es decir, producir el mismo efecto, en una gran cantidad de bibliotecas de expresiones regulares. I-Regexp también se limita a la coincidencia, es decir, a proporcionar una coincidencia verdadera o falsa entre una expresión regular y un fragmento de texto determinado. Por lo tanto, carece de funciones avanzadas como grupos de captura, búsqueda anticipada y referencias inversas. [43]
Muchas de las características que se encuentran en prácticamente todas las bibliotecas de expresiones regulares modernas proporcionan un poder expresivo que supera a los lenguajes regulares . Por ejemplo, muchas implementaciones permiten agrupar subexpresiones con paréntesis y recordar el valor con el que coinciden en la misma expresión (referencias inversas ). Esto significa que, entre otras cosas, un patrón puede coincidir con cadenas de palabras repetidas como "papa" o "WikiWiki", llamadascuadradosen la teoría del lenguaje formal. El patrón para estas cadenas es(.+)\1.
El lenguaje de los cuadrados no es regular ni está libre de contexto , debido al lema de bombeo . Sin embargo, la coincidencia de patrones con un número ilimitado de referencias hacia atrás, como lo admiten numerosas herramientas modernas, aún es sensible al contexto . [44] El problema general de hacer coincidir cualquier número de referencias hacia atrás es NP-completo , y el tiempo de ejecución de los algoritmos conocidos crece exponencialmente con el número de grupos de referencias hacia atrás utilizados. [45]
Sin embargo, muchas herramientas, bibliotecas y motores que proporcionan este tipo de construcciones aún utilizan el término expresión regular para sus patrones. Esto ha dado lugar a una nomenclatura en la que el término expresión regular tiene diferentes significados en la teoría del lenguaje formal y en la comparación de patrones. Por este motivo, algunas personas han empezado a utilizar el término regex , regexp o simplemente patrón para describir este último. Larry Wall , autor del lenguaje de programación Perl, escribe en un ensayo sobre el diseño de Raku:
Las "expresiones regulares" […] están relacionadas sólo marginalmente con las expresiones regulares reales. Sin embargo, el término ha crecido con las capacidades de nuestros motores de comparación de patrones, por lo que no intentaré luchar contra la necesidad lingüística aquí. Sin embargo, las llamaré, en general, "regexes" (o "regexen", cuando esté de humor anglosajón). [19]
Otras características que no se encuentran en la descripción de lenguajes regulares incluyen aserciones. Estas incluyen las ubicuas ^y $, utilizadas desde al menos 1970, [46] así como algunas extensiones más sofisticadas como lookaround que aparecieron en 1994. [47] Los lookarounds definen el entorno de una coincidencia y no se extienden a la coincidencia en sí, una característica solo relevante para el caso de uso de búsqueda de cadenas. [ cita requerida ] Algunas de ellas pueden simularse en un lenguaje regular tratando el entorno como parte del lenguaje también. [48]
ElLas afirmaciones de look-ahead (?=...) y(?!...)han sido atestiguadas desde al menos 1994, comenzando con Perl 5. [47] Las afirmaciones de look-behind(?<=...)y(?<!...)están atestiguadas desde 1997 en una confirmación de Ilya Zakharevich en Perl 5.005. [49]
Hay al menos tres algoritmos diferentes que deciden si una expresión regular determinada coincide con una cadena y de qué manera.
El más antiguo y rápido se basa en un resultado de la teoría del lenguaje formal que permite transformar cada autómata finito no determinista (AFN) en un autómata finito determinista (AFD). El AFD se puede construir explícitamente y luego ejecutar en la cadena de entrada resultante un símbolo a la vez. Construir el AFD para una expresión regular de tamaño m tiene un costo de tiempo y memoria de O (2 m ), pero se puede ejecutar en una cadena de tamaño n en un tiempo O ( n ). Nótese que el tamaño de la expresión es el tamaño después de que se hayan expandido las abreviaturas, como los cuantificadores numéricos.
Un enfoque alternativo es simular el NFA directamente, esencialmente construyendo cada estado del DFA a pedido y luego descartándolo en el siguiente paso. Esto mantiene el DFA implícito y evita el costo de construcción exponencial, pero el costo de ejecución aumenta a O ( mn ). El enfoque explícito se llama algoritmo DFA y el enfoque implícito algoritmo NFA. Agregar almacenamiento en caché al algoritmo NFA a menudo se llama algoritmo "DFA perezoso", o simplemente algoritmo DFA sin hacer una distinción. Estos algoritmos son rápidos, pero usarlos para recuperar subexpresiones agrupadas, cuantificación perezosa y características similares es complicado. [50] [51] Las implementaciones modernas incluyen la familia re1- re2 -sregex basada en el código de Cox.
El tercer algoritmo consiste en hacer coincidir el patrón con la cadena de entrada mediante un retroceso . Este algoritmo se denomina comúnmente NFA, pero esta terminología puede resultar confusa. Su tiempo de ejecución puede ser exponencial, lo que se observa en implementaciones simples cuando se realiza una comparación con expresiones como esta que contienen tanto alternancia como cuantificación ilimitada y obligan al algoritmo a considerar una cantidad exponencialmente creciente de subcasos. Este comportamiento puede causar un problema de seguridad denominado Denegación de servicio por expresión regular (ReDoS).(a|aa)*b
Aunque las implementaciones de retroceso sólo dan una garantía exponencial en el peor de los casos, proporcionan una flexibilidad y un poder expresivo mucho mayores. Por ejemplo, cualquier implementación que permita el uso de referencias hacia atrás, o implemente las diversas extensiones introducidas por Perl, debe incluir algún tipo de retroceso. Algunas implementaciones intentan proporcionar lo mejor de ambos algoritmos ejecutando primero un algoritmo DFA rápido y revirtiendo a un algoritmo de retroceso potencialmente más lento sólo cuando se encuentra una referencia hacia atrás durante la coincidencia. GNU grep (y el DFA gnulib subyacente) utiliza una estrategia de este tipo. [52]
Se han logrado algoritmos de tiempo de ejecución sublineales utilizando algoritmos basados en Boyer-Moore (BM) y técnicas de optimización DFA relacionadas, como el escaneo inverso. [53] GNU grep, que admite una amplia variedad de sintaxis y extensiones POSIX, utiliza BM para un prefiltrado de primer paso y luego utiliza un DFA implícito. Wu agrep , que implementa la coincidencia aproximada, combina el prefiltrado en el DFA en BDM (coincidencia DAWG hacia atrás). El BNDM de NR-grep extiende la técnica BDM con paralelismo a nivel de bit Shift-Or. [54]
Existen algunas alternativas teóricas al retroceso para las retrorreferencias, y sus "exponentes" son más moderados en el sentido de que solo están relacionados con el número de retrorreferencias, una propiedad fija de algunos lenguajes de expresiones regulares como POSIX. Un método ingenuo que duplica un NFA sin retroceso para cada nota de retrorreferencia tiene una complejidad de tiempo y espacio para un pajar de longitud n y k retrorreferencias en la expresión regular. [55] Un trabajo teórico muy reciente basado en autómatas de memoria proporciona un límite más estricto basado en nodos de variables "activas" utilizados y una posibilidad polinómica para algunas expresiones regulares retrorreferenciadas. [56]
En términos teóricos, cualquier conjunto de símbolos puede coincidir con expresiones regulares siempre que esté predefinido. En términos de implementaciones históricas, las expresiones regulares se escribieron originalmente para usar caracteres ASCII como su conjunto de símbolos, aunque las bibliotecas de expresiones regulares han admitido muchos otros conjuntos de caracteres . Muchos motores de expresiones regulares modernos ofrecen al menos algún soporte para Unicode . En la mayoría de los aspectos, no importa cuál sea el conjunto de caracteres, pero surgen algunos problemas al ampliar las expresiones regulares para que admitan Unicode.
[x-y]son válidos siempre que x e y tengan puntos de código en el rango [0x00,0x7F] y codepoint( x ) ≤ codepoint( y ). La extensión natural de dichos rangos de caracteres a Unicode simplemente cambiaría el requisito de que los puntos finales se encuentren en [0x00,0x7F] al requisito de que se encuentren en [0x0000,0x10FFFF]. Sin embargo, en la práctica, esto no suele ser así. Algunas implementaciones, como la de gawk , no permiten que los rangos de caracteres crucen bloques Unicode. Un rango como [0x61,0x7F] es válido ya que ambos puntos finales caen dentro del bloque de latín básico, al igual que [0x0530,0x0560] ya que ambos puntos finales caen dentro del bloque de armenio, pero un rango como [0x0061,0x0532] no es válido ya que incluye múltiples bloques Unicode. Otros motores, como el del editor Vim , permiten el cruce de bloques pero los valores de caracteres no deben estar separados por más de 256 caracteres. [57]java.util.regexbiblioteca, las propiedades de la forma \p{InX}o \p{Block=X}coinciden con caracteres del bloque X y \P{InX}o \P{Block=X}coinciden con puntos de código que no están en ese bloque. De manera similar, \p{Armenian}, \p{IsArmenian}, o \p{Script=Armenian}coincide con cualquier carácter en el script armenio. En general, \p{X}coincide con cualquier carácter con la propiedad binaria X o la categoría general X . Por ejemplo, \p{Lu}, \p{Uppercase_Letter}, o \p{GC=Lu}coincide con cualquier letra mayúscula. Las propiedades binarias que no son categorías generales incluyen \p{White_Space}, \p{Alphabetic}, \p{Math}, y \p{Dash}. Ejemplos de propiedades no binarias son \p{Bidi_Class=Right_to_Left}, \p{Word_Break=A_Letter}, y \p{Numeric_Value=10}.La mayoría de los lenguajes de programación de propósito general admiten capacidades de expresiones regulares, ya sea de forma nativa o a través de bibliotecas . Se incluye soporte integral en:
Las expresiones regulares son útiles en una amplia variedad de tareas de procesamiento de texto y, más generalmente, en el procesamiento de cadenas , donde los datos no necesitan ser textuales. Las aplicaciones comunes incluyen la validación de datos , el raspado de datos (especialmente el raspado web ), la manipulación de datos , el análisis simple , la producción de sistemas de resaltado de sintaxis y muchas otras tareas.
Algunos programas de edición de escritorio de alta gama tienen la capacidad de usar expresiones regulares para aplicar estilos de texto automáticamente, lo que evita que la persona que realiza el diseño deba realizar el trabajo a mano para cualquier cosa que pueda coincidir con una expresión regular. Por ejemplo, al definir un estilo de carácter que convierta el texto en versalitas y luego usar la expresión regular [A-Z]{4,}para aplicar ese estilo, cualquier palabra de cuatro o más letras mayúsculas consecutivas se representará automáticamente como versalitas.
Si bien las expresiones regulares serían útiles en los motores de búsqueda de Internet , procesarlas en toda la base de datos podría consumir recursos informáticos excesivos según la complejidad y el diseño de la expresión regular. Aunque en muchos casos los administradores de sistemas pueden ejecutar consultas basadas en expresiones regulares internamente, la mayoría de los motores de búsqueda no ofrecen soporte para expresiones regulares al público. Las excepciones notables incluyen Google Code Search y Exalead . Sin embargo, Google Code Search se cerró en enero de 2012. [69]
Las reglas de sintaxis específicas varían según la implementación, el lenguaje de programación o la biblioteca en uso. Además, la funcionalidad de las implementaciones de expresiones regulares puede variar entre versiones .
Dado que las expresiones regulares pueden resultar difíciles de explicar y comprender sin ejemplos, los sitios web interactivos para probarlas son un recurso útil para aprenderlas mediante la experimentación. Esta sección proporciona una descripción básica de algunas de las propiedades de las expresiones regulares a modo de ilustración.
En los ejemplos se utilizan las siguientes convenciones. [70]
metacaracter(es) ;; la columna de metacaracteres especifica la sintaxis de expresiones regulares que se está demostrando=~ m// ;; indica una operación de coincidencia de expresiones regulares en Perl=~ s/// ;; indica una operación de sustitución de expresiones regulares en Perl
También vale la pena señalar que estas expresiones regulares tienen una sintaxis similar a la de Perl. Las expresiones regulares POSIX estándar son diferentes.
A menos que se indique lo contrario, los siguientes ejemplos se ajustan al lenguaje de programación Perl , versión 5.8.8, 31 de enero de 2006. Esto significa que otras implementaciones pueden carecer de soporte para algunas partes de la sintaxis que se muestra aquí (por ejemplo, regex básico vs. extendido, \( \)vs. ()o falta de \den lugar de POSIX [:digit:] ).
La sintaxis y las convenciones utilizadas en estos ejemplos coinciden también con las de otros entornos de programación. [71]
Las expresiones regulares a menudo se pueden crear ("inducir" o "aprender") basándose en un conjunto de cadenas de ejemplo. Esto se conoce como la inducción de lenguajes regulares y es parte del problema general de inducción gramatical en la teoría del aprendizaje computacional . Formalmente, dados ejemplos de cadenas en un lenguaje regular, y quizás también dados ejemplos de cadenas que no están en ese lenguaje regular, es posible inducir una gramática para el lenguaje, es decir, una expresión regular que genere ese lenguaje. No todos los lenguajes regulares se pueden inducir de esta manera (ver identificación de lenguaje en el límite ), pero muchos sí. Por ejemplo, el conjunto de ejemplos {1, 10, 100} y el conjunto negativo (de contraejemplos) {11, 1001, 101, 0} se pueden usar para inducir la expresión regular 1⋅0* (1 seguido de cero o más 0).
El concepto de eventos regulares fue introducido por Kleene a través de la definición de expresiones regulares.
válida para expresiones regulares extendidas, incluso si no describen una clase más grande que los lenguajes regulares; cf. p.121.
Digresión: coincidencia de subtipos POSIX
el escáner detecta una transición en backref, devuelve una especie de "semi-éxito" que indica que la coincidencia deberá verificarse con un comparador de backtracking.
m/[^abc]/también podría representarse como /[^abc]/. La 'm' sólo es necesaria si el usuario desea especificar una operación de coincidencia sin utilizar una barra diagonal como delimitador de expresiones regulares . A veces es útil especificar un delimitador de expresiones regulares alternativo para evitar " colisiones de delimitadores ". Consulte 'perldoc perlre Archivado el 31 de diciembre de 2009 en Wayback Machine ' para obtener más detalles.