Umbral de error (evolución)

Límite teórico de la tasa de mutación.

En biología evolutiva y genética de poblaciones , el umbral de error (o tasa de mutación crítica ) es un límite en el número de pares de bases que una molécula autorreplicante puede tener antes de que la mutación destruya la información en las generaciones posteriores de la molécula. El umbral de error es crucial para comprender la "paradoja de Eigen".

El umbral de error es un concepto en los orígenes de la vida ( abiogénesis ), en particular de la vida muy temprana, antes de la llegada del ADN . Se postula que las primeras moléculas autorreplicantes podrían haber sido pequeñas moléculas de ARN similares a ribozimas . Estas moléculas constan de cadenas de pares de bases o "dígitos" y su orden es un código que dirige cómo la molécula interactúa con su entorno. Toda replicación está sujeta a errores de mutación. Durante el proceso de replicación, cada dígito tiene una cierta probabilidad de ser reemplazado por algún otro dígito, lo que cambia la forma en que la molécula interactúa con su entorno y puede aumentar o disminuir su aptitud o capacidad de reproducirse en ese entorno.

Paisaje de fitness

Manfred Eigen señaló en su artículo de 1971 (Eigen 1971) que este proceso de mutación impone un límite al número de dígitos que puede tener una molécula. Si una molécula excede este tamaño crítico, el efecto de las mutaciones se vuelve abrumador y un proceso de mutación desbocado destruirá la información en las generaciones posteriores de la molécula. El umbral de error también está controlado por el "panorama de aptitud" de las moléculas. El panorama del fitness se caracteriza por los dos conceptos de altura (=fitness) y distancia (=número de mutaciones). Las moléculas similares están "cerca" unas de otras, y las moléculas que son más aptas que otras y tienen más probabilidades de reproducirse, están "más arriba" en el paisaje.

Si una secuencia particular y sus vecinos tienen una alta aptitud, formarán una cuasiespecie y podrán soportar longitudes de secuencia más largas que una secuencia ajustada con pocos vecinos aptos, o una vecindad de secuencias menos ajustadas. Además, Wilke (Wilke 2005) señaló que el concepto de umbral de error no se aplica en partes del paisaje donde hay mutaciones letales, en las que la mutación inducida produce una aptitud nula y prohíbe que la molécula se reproduzca.

La paradoja de Eigen

La paradoja de Eigen es uno de los enigmas más difíciles de resolver en el estudio de los orígenes de la vida. Se cree que el concepto de umbral de error descrito anteriormente limita el tamaño de las moléculas autorreplicantes a unos pocos cientos de dígitos, pero casi toda la vida en la Tierra requiere moléculas mucho más largas para codificar su información genética. Este problema se maneja en las células vivas mediante enzimas que reparan mutaciones, permitiendo que las moléculas codificantes alcancen tamaños del orden de millones de pares de bases. Estas grandes moléculas deben, por supuesto, codificar las mismas enzimas que las reparan, y aquí radica la paradoja de Eigen, expuesta por primera vez por Manfred Eigen en su artículo de 1971 (Eigen 1971). ^[1] En pocas palabras, la paradoja de Eigen equivale a lo siguiente:

• Sin enzimas correctoras de errores, el tamaño máximo de una molécula replicante es de unos 100 pares de bases.
• Para que una molécula replicante codifique enzimas correctoras de errores, debe tener un tamaño sustancialmente mayor a 100 bases.

Esta es una especie de paradoja del huevo o la gallina , con una solución aún más difícil. ¿Qué fue primero, el genoma grande o las enzimas correctoras de errores? Se han propuesto varias soluciones a esta paradoja:

• Modelo corrector estocástico (Szathmáry & Maynard Smith, 1995). En esta solución propuesta, varias moléculas primitivas de, digamos, dos tipos diferentes, están asociadas entre sí de alguna manera, tal vez mediante una cápsula o "pared celular". Si su éxito reproductivo mejora al tener, digamos, números iguales en cada célula, y la reproducción ocurre por división en la que cada uno de los diversos tipos de moléculas se distribuye aleatoriamente entre los "hijos", el proceso de selección promoverá esa representación igual en el células, aunque una de las moléculas pueda tener una ventaja selectiva sobre la otra.
• Umbral de error relajado (Kun et al., 2005): los estudios de ribozimas reales indican que la tasa de mutación puede ser sustancialmente menor de lo esperado inicialmente, del orden de 0,001 por par de bases por replicación. Esto puede permitir longitudes de secuencia del orden de 7 a 8 mil pares de bases, suficientes para incorporar enzimas rudimentarias de corrección de errores.

Un modelo matemático simple

Considere una molécula de 3 dígitos [A,B,C] donde A, B y C pueden tomar los valores 0 y 1. Hay ocho secuencias de este tipo ([000], [001], [010], [011] , [100], [101], [110] y [111]). Digamos que la molécula [000] es la más apta; en cada replicación produce un promedio de copias, donde . Esta molécula se llama "secuencia maestra". Las otras siete secuencias son menos aptas; cada uno de ellos produce sólo 1 copia por replicación. La replicación de cada uno de los tres dígitos se realiza con una tasa de mutación de μ. En otras palabras, en cada replicación de un dígito de una secuencia, existe la probabilidad de que sea erróneo; 0 será reemplazado por 1 o viceversa. Ignoremos las mutaciones dobles y la muerte de las moléculas (la población crecerá infinitamente) y dividamos las ocho moléculas en tres clases dependiendo de su distancia de Hamming de la secuencia maestra: ${\displaystyle a}$ ${\displaystyle a>1}$ ${\displaystyle \mu }$

Tenga en cuenta que el número de secuencias para la distancia d es solo el coeficiente binomial para L=3, y que cada secuencia se puede visualizar como el vértice de un cubo tridimensional L=3, donde cada arista del cubo especifica una ruta de mutación en la que cambiar la distancia de Hamming es cero o ±1. Se puede observar que, por ejemplo, un tercio de las mutaciones de las moléculas [001] producirán moléculas [000], mientras que los otros dos tercios producirán las moléculas de clase 2 [011] y [101]. Ahora podemos escribir la expresión para las poblaciones hijas de la clase i en términos de las poblaciones padres . ${\displaystyle {\tbinom {L}{d}}}$ ${\displaystyle n'_{i}}$ ${\displaystyle n_{j}}$

${\displaystyle n'_{i}=\sum _{j=0}^{3}w_{ij}n_{j}}$

donde la matriz ' w ' que incorpora la selección natural y la mutación, según modelo de cuasiespecies , viene dada por:

${\displaystyle \mathbf {w} ={\begin{bmatrix}a\cdot Q&3a\cdot \mu &0&0\\\mu &Q&2\mu &0\\0&2\mu &Q&\mu \\0&0&3\mu &Q\end{bmatrix}}}$

¿Dónde está la probabilidad de que una molécula completa se replique con éxito? Los vectores propios de la matriz w producirán los números de población de equilibrio para cada clase. Por ejemplo, si la tasa de mutación μ es cero, tendremos Q=1 y las concentraciones de equilibrio serán . La secuencia maestra, siendo el más apto será el único que sobreviva. Si tenemos una fidelidad de replicación de Q=0,95 y una ventaja genética de a=1,05, entonces las concentraciones de equilibrio serán aproximadamente . Se puede observar que la secuencia maestra no es tan dominante; sin embargo, las secuencias con baja distancia de Hamming son mayoritarias. Si tenemos una fidelidad de replicación de Q cercana a 0, entonces las concentraciones de equilibrio serán aproximadamente . Esta es una población con el mismo número de cada una de las 8 secuencias. (Si tuviéramos una población perfectamente igual de todas las secuencias, tendríamos poblaciones de [1,3,3,1]/8). ${\displaystyle Q=(1-\mu )^{L}}$ ${\displaystyle [n_{0},n_{1},n_{2},n_{3}]=[1,0,0,0]}$ ${\displaystyle [0.33,0.38,0.24,0.06]}$ ${\displaystyle [0.125,0.375,0.375,0.125]}$

Si ahora vamos al caso donde el número de pares de bases es grande, digamos L=100, obtenemos un comportamiento que se asemeja a una transición de fase . El gráfico siguiente a la izquierda muestra una serie de concentraciones de equilibrio divididas por el coeficiente binomial . (Esta multiplicación mostrará la población de una secuencia individual a esa distancia y producirá una línea plana para una distribución igual). La ventaja selectiva de la secuencia maestra se establece en a=1,05. El eje horizontal es la distancia de Hamming d  . Las distintas curvas corresponden a distintas tasas de mutación totales . Se ve que para valores bajos de la tasa de mutación total, la población consiste en una cuasiespecie reunida en las proximidades de la secuencia maestra. Por encima de una tasa de mutación total de aproximadamente 1-Q=0,05, la distribución se extiende rápidamente para poblar todas las secuencias por igual. El gráfico siguiente a la derecha muestra la población fraccionaria de la secuencia maestra en función de la tasa de mutación total. Nuevamente se ve que por debajo de una tasa de mutación crítica de aproximadamente 1-Q=0,05, la secuencia maestra contiene a la mayor parte de la población, mientras que por encima de esta tasa, contiene sólo alrededor de la población total. ${\displaystyle {\tbinom {100}{k}}}$ ${\displaystyle (1-Q)}$ ${\displaystyle 2^{-L}\approx 10^{-30}}$

Números de población en función de la distancia d de Hamming y la tasa de mutación (1-Q). El eje horizontal d   es la distancia de Hamming de las secuencias moleculares de la secuencia maestra. El eje vertical es el logaritmo de la población para cualquier secuencia a esa distancia dividido por la población total (de ahí la división de n _d por el coeficiente binomial). El número total de dígitos por secuencia es L=100 y la secuencia maestra tiene una ventaja selectiva de a=1,05.

La población de la secuencia maestra como fracción de la población total ( n ) en función de la tasa de mutación general (1-Q). El número total de dígitos por secuencia es L=100 y la secuencia maestra tiene una ventaja selectiva de a=1,05. Se ve que la "transición de fase" ocurre aproximadamente en 1-Q=0,05.

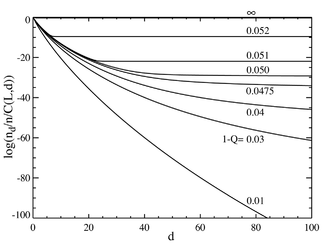
Se puede observar que hay una transición brusca en un valor de 1-Q   un poco mayor que 0,05. Para tasas de mutación superiores a este valor, la población de la secuencia maestra cae prácticamente a cero. Por encima de este valor, domina.

En el límite, cuando L se acerca al infinito, el sistema de hecho tiene una transición de fase en un valor crítico de Q :. Se podría pensar en la tasa de mutación general (1-Q) como una especie de "temperatura" que "derrite" la fidelidad de las secuencias moleculares por encima de la "temperatura" crítica de . Para que se produzca una replicación fiel, la información debe estar "congelada" en el genoma. ${\displaystyle Q_{c}=1/a.}$ ${\displaystyle 1-Q_{c}}$

Ver también

• Catástrofe de errores
• Vórtice de extinción
• Entropía genética
• Erosión genética
• trinquete de muller

Referencias

1. Holmes, Edward C. (2009). La evolución y aparición de los virus de ARN. Prensa de la Universidad de Oxford. págs.22, 23, 48. ISBN 9780199211128. Consultado el 1 de febrero de 2019 .

• Eigen, M. (1971). "Autoorganización de la materia y evolución de Macromoléculas biológicas". Naturwissenschaften . 58 (10): 465–523. Código bibliográfico : 1971NW.....58..465E. doi :10.1007/BF00623322. PMID  4942363. S2CID  38296619.
• "Teoría de las cuasiespecies en el contexto de la genética de poblaciones - Claus O. Wilke" (PDF) . Consultado el 12 de octubre de 2005 .
• Campos, PRA; Fontanari, JF (1999). "Escalado de tamaño finito de la transición del umbral de error en poblaciones finitas" (PDF) . J. Física. R: Matemáticas. Gen.​ 32 (1): L1–L7. arXiv : cond-mat/9809209 . Código Bib : 1999JPhA...32L...1C. doi :10.1088/0305-4470/32/1/001. S2CID  16500591.
• Holmes, Edward C. (2005). "Sobre tener la talla adecuada". Genética de la Naturaleza . 37 (9): 923–924. doi :10.1038/ng0905-923. PMC  7097767 . PMID  16132047.
• Eörs Szathmáry; John Maynard Smith (1995). "Las grandes transiciones evolutivas". Naturaleza . 374 (6519): 227–232. Código Bib :1995Natur.374..227S. doi :10.1038/374227a0. PMID  7885442. S2CID  4315120.
• Luis Villareal; Günther Witzany (2013). "Repensar la teoría de las cuasiespecies: del tipo más apto a los consorcios cooperativos". Revista Mundial de Química Biológica . 4 (4): 79–90. doi : 10.4331/wjbc.v4.i4.79 . PMC  3856310 . PMID  24340131.
• Ádám Kun; Mauro Santos; Eörs Szathmáry (2005). "Las ribozimas reales sugieren un umbral de error relajado". Genética de la Naturaleza . 37 (9): 1008–1011. doi :10.1038/ng1621. PMID  16127452. S2CID  30582475.