En topología algebraica , un subgrupo periférico para un par espacio-subespacio X ⊃ Y es un cierto subgrupo del grupo fundamental del espacio complementario, π 1 ( X − Y ). Su clase de conjugación es un invariante del par ( X , Y ). Es decir, cualquier homeomorfismo ( X , Y ) → ( X ′, Y ′) induce un isomorfismo π 1 ( X − Y ) → π 1 ( X ′ − Y ′) llevando subgrupos periféricos a subgrupos periféricos.
Un subgrupo periférico consiste en bucles en X − Y que son periféricos a Y , es decir, que permanecen "cerca" de Y (excepto cuando pasan hacia y desde el punto base ). Cuando se especifica un conjunto ordenado de generadores para un subgrupo periférico, el subgrupo y los generadores se denominan colectivamente un sistema periférico para el par ( X , Y ).
Los sistemas periféricos se utilizan en la teoría de nudos como un invariante algebraico completo de nudos. Existe una forma sistemática de elegir generadores para un subgrupo periférico de un nudo en el espacio tridimensional , de modo que los distintos tipos de nudos siempre tengan sistemas periféricos algebraicamente distintos. Los generadores en esta situación se denominan longitud y meridiano del complemento del nudo .

Sea Y un subespacio del espacio topológico conexo por caminos X , cuyo complemento X − Y es conexo por caminos. Fijemos un punto base x ∈ X − Y . Para cada componente de camino V i de X − Y ∩ Y , elijamos un camino γ i desde x hasta un punto en V i . Un elemento [α] ∈ π 1 ( X − Y , x ) se llama periférico con respecto a esta elección si está representado por un bucle en U ∪ ∪ i γ i para cada entorno U de Y . El conjunto de todos los elementos periféricos con respecto a una elección dada forma un subgrupo de π 1 ( X − Y , x ), llamado subgrupo periférico .
En el diagrama, un bucle periférico comenzaría en el punto base x y recorrería el camino γ hasta estar dentro del entorno U del subespacio Y. Luego, se movería por U como quisiera (evitando Y ). Finalmente, regresaría al punto base x a través de γ. Dado que U puede ser una envoltura muy estrecha alrededor de Y , el bucle tiene que permanecer cerca de Y.
Dos subgrupos periféricos cualesquiera de π 1 ( X − Y , x ), resultantes de diferentes elecciones de caminos γ i , son conjugados en π 1 ( X − Y , x ). Además, cada conjugado de un subgrupo periférico es en sí mismo periférico con respecto a alguna elección de caminos γ i . Por lo tanto, la clase de conjugación del subgrupo periférico es un invariante del par ( X , Y ).
Un subgrupo periférico, junto con un conjunto ordenado de generadores , se denomina sistema periférico para el par ( X , Y ). Si se especifica un método sistemático para seleccionar estos generadores, el sistema periférico es, en general, un invariante más fuerte que el subgrupo periférico solo. De hecho, es un invariante completo para los nudos.

Los subgrupos periféricos para un nudo domesticado K en R 3 son isomorfos a Z ⊕ Z si el nudo no es trivial, Z si es el nudo no trivial . Son generados por dos elementos, llamados longitud [ l ] y meridiano [ m ]. (Si K es el nudo no trivial, entonces [ l ] es una potencia de [ m ], y un subgrupo periférico es generado por [ m ] solo.) Una longitud es un bucle que corre desde el punto base x a lo largo de un camino γ hasta un punto y en el límite de un vecindario tubular de K , luego sigue a lo largo del tubo, haciendo una vuelta completa para regresar a y , luego regresa a x a través de γ. Un meridiano es un bucle que corre desde x a y , luego gira alrededor del tubo, regresa a y , luego regresa a x . (La propiedad de ser una longitud o meridiano está bien definida porque los vecindarios tubulares de un nudo domesticado son todos ambientalmente isotópicos ). Nótese que cada grupo de nudos tiene una longitud y un meridiano; si [ l ] y [ m ] son una longitud y un meridiano en un subgrupo periférico dado, entonces también lo son [ l ]·[ m ] n y [ m ] −1 , respectivamente ( n ∈ Z ). De hecho, estas son las únicas longitudes y meridianos en el subgrupo, y cualquier par generará el subgrupo.
Un sistema periférico para un nudo puede seleccionarse eligiendo generadores [ l ] y [ m ] tales que la longitud l tenga número de enlace 0 con K , y la terna ordenada ( m′ , l′ , n ) sea una base orientada positivamente para R 3 , donde m′ es el vector tangente de m basado en y , l′ es el vector tangente de l basado en y , y n es una normal que apunta hacia afuera al tubo en y . (Suponga que los representantes l y m se eligen para que sean suaves en el tubo y se crucen solo en y .) Si se eligen así, el sistema periférico es un invariante completo para nudos, como se demuestra en [Waldhausen 1968].

El nudo cuadrado y el nudo de abuela son nudos distintos y tienen complementos no homeomorfos . Sin embargo, sus grupos de nudos son isomorfos. No obstante, en [Fox 1961] se demostró que ningún isomorfismo de sus grupos de nudos lleva un subgrupo periférico de uno a un subgrupo periférico del otro. Por lo tanto, el subgrupo periférico es suficiente para distinguir estos nudos.
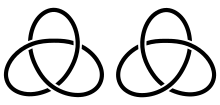
El trébol y su imagen especular son nudos distintos y, en consecuencia, no existe un homeomorfismo que preserve la orientación entre sus complementos. Sin embargo, existe un autohomeomorfismo de R 3 que invierte la orientación y que lleva al trébol a su imagen especular. Este homeomorfismo induce un isomorfismo de los grupos de nudos, que lleva un subgrupo periférico a un subgrupo periférico, una longitud a una longitud y un meridiano a un meridiano. Por lo tanto, el subgrupo periférico no es suficiente para distinguir estos nudos. No obstante, se demostró en [Dehn 1914] que ningún isomorfismo de estos grupos de nudos preserva el sistema periférico seleccionado como se describió anteriormente. Un isomorfismo, en el mejor de los casos, llevará un generador a un generador que va en la "dirección equivocada". Por lo tanto, el sistema periférico puede distinguir estos nudos.
Es posible expresar longitudes y meridianos de un nudo como palabras en la presentación de Wirtinger del grupo de nudos, sin referencia al nudo en sí.