La comunidad científica examinó varios enfoques para redefinir el kilogramo antes de decidir una revisión del SI en noviembre de 2018. Cada enfoque tenía ventajas y desventajas.
Antes de la redefinición, el kilogramo y otras unidades del SI basadas en el kilogramo se definían mediante un objeto metálico artificial llamado prototipo internacional del kilogramo (IPK). [1] Hubo un amplio acuerdo en que se debía reemplazar la antigua definición del kilogramo.
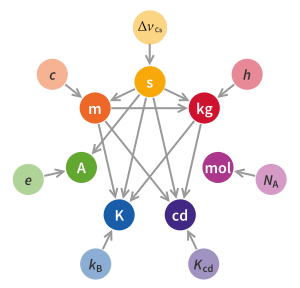
El Comité Internacional de Pesas y Medidas (CIPM) aprobó una redefinición de las unidades base del SI en noviembre de 2018 que define el kilogramo definiendo la constante de Planck como exactamente6.626 070 15 × 10 −34 kg⋅m 2 ⋅s −1 . Este enfoque define efectivamente el kilogramo en términos del segundo y el metro , y entró en vigor el 20 de mayo de 2019. [1] [2] [3] [4]
En 1960, el metro, que anteriormente se había definido de manera similar con referencia a una única barra de platino-iridio con dos marcas, se redefinió en términos de una constante física invariante (la longitud de onda de una emisión particular de luz emitida por el criptón , [5] y más tarde la velocidad de la luz ) de modo que el estándar se pueda reproducir independientemente en diferentes laboratorios siguiendo una especificación escrita.
En la 94ª Reunión del Comité Internacional de Pesas y Medidas (CIPM) en 2005, se recomendó que se hiciera lo mismo con el kilogramo. [6]
En octubre de 2010, el CIPM votó para presentar una resolución para su consideración en la Conferencia General de Pesas y Medidas (CGPM), para "tomar nota de una intención" de que el kilogramo se defina en términos de la constante de Planck , h (que tiene dimensiones de energía por tiempo) junto con otras constantes físicas. [7] [8] Esta resolución fue aceptada por la 24.ª conferencia de la CGPM [9] en octubre de 2011 y se debatió más a fondo en la 25.ª conferencia en 2014. [10] [11] Aunque el Comité reconoció que se había logrado un progreso significativo, concluyó que los datos aún no parecían lo suficientemente sólidos como para adoptar la definición revisada, y que el trabajo debería continuar para permitir la adopción en la 26.ª reunión, programada para 2018. [10] Una definición de este tipo permitiría teóricamente que se utilizara cualquier aparato que fuera capaz de delinear el kilogramo en términos de la constante de Planck, siempre que tuviera suficiente precisión, exactitud y estabilidad. La balanza Kibble es una forma de hacerlo.
Como parte de este proyecto, se consideraron y exploraron durante muchos años una variedad de tecnologías y enfoques muy diferentes. Algunos de estos enfoques se basaban en equipos y procedimientos que habrían permitido la producción reproducible de nuevos prototipos de masa de kilogramos a pedido utilizando técnicas de medición y propiedades de materiales que en última instancia se basan en constantes físicas o son trazables a ellas. Otros se basaban en dispositivos que medían la aceleración o el peso de masas de prueba de kilogramos ajustadas a mano y que expresaban sus magnitudes en términos eléctricos mediante componentes especiales que permiten la trazabilidad a constantes físicas. Estos enfoques dependen de la conversión de una medición de peso en una masa y, por lo tanto, requieren la medición precisa de la fuerza de la gravedad en laboratorios. Todos los enfoques habrían fijado con precisión una o más constantes de la naturaleza en un valor definido.

La balanza Kibble (conocida como "balanza de vatios" antes de 2016) es esencialmente una báscula de un solo platillo que mide la potencia eléctrica necesaria para oponerse al peso de una masa de prueba de un kilogramo cuando es atraída por la gravedad de la Tierra. Es una variación de una balanza de amperios , con un paso de calibración adicional que elimina el efecto de la geometría. El potencial eléctrico en la balanza Kibble está delineado por un estándar de voltaje Josephson , que permite vincular el voltaje a una constante invariante de la naturaleza con una precisión y estabilidad extremadamente altas. Su resistencia de circuito está calibrada contra un estándar de resistencia de efecto Hall cuántico .
La balanza Kibble requiere una medición extremadamente precisa de la aceleración gravitacional local g en el laboratorio, utilizando un gravímetro . Por ejemplo, cuando la elevación del centro del gravímetro difiere de la de la masa de prueba cercana en la balanza Kibble, el NIST compensa el gradiente de gravedad de la Tierra de309 μGal /m , lo que afecta el peso de una masa de prueba de un kilogramo en aproximadamente316 μg/m3 .
En abril de 2007, la implementación de la balanza Kibble por parte del NIST demostró una incertidumbre estándar relativa combinada (CRSU) de 36 μg. [12] [Nota 1] La balanza Kibble del Laboratorio Nacional de Física del Reino Unido demostró una CRSU de 70,3 μg en 2007. [13] Esa balanza Kibble se desarmó y se envió en 2009 al Instituto de Estándares Nacionales de Medición de Canadá (parte del Consejo Nacional de Investigación ), donde la investigación y el desarrollo con el dispositivo pudieron continuar.
La virtud de las realizaciones electrónicas como la balanza Kibble es que la definición y difusión del kilogramo ya no depende de la estabilidad de prototipos de kilogramos, que deben manipularse y almacenarse con mucho cuidado. Libera a los físicos de la necesidad de depender de suposiciones sobre la estabilidad de esos prototipos. En cambio, los patrones de masa ajustados a mano y de aproximación cercana pueden simplemente pesarse y documentarse como iguales a un kilogramo más un valor de compensación. Con la balanza Kibble, mientras que el kilogramo se delinea en términos eléctricos y gravitacionales, todos los cuales son atribuibles a invariantes de la naturaleza, se define de una manera que es directamente atribuible a tres constantes fundamentales de la naturaleza. La constante de Planck define el kilogramo en términos del segundo y el metro. Al fijar la constante de Planck, la definición del kilogramo depende además solo de las definiciones del segundo y el metro. La definición del segundo depende de una única constante física definida: la frecuencia de desdoblamiento hiperfino del estado fundamental del átomo de cesio-133 Δ ν ( 133 Cs) hfs . El metro depende del segundo y de una constante física definida adicional: la velocidad de la luz c . Con el kilogramo redefinido de esta manera, los objetos físicos como el IPK ya no forman parte de la definición, sino que se convierten en estándares de transferencia .
Las balanzas como la balanza Kibble también permiten una mayor flexibilidad a la hora de elegir materiales con propiedades especialmente deseables para los patrones de masa. Por ejemplo, se podría seguir utilizando Pt‑10Ir para que la gravedad específica de los patrones de masa recién producidos fuera la misma que la de los patrones nacionales primarios y de control existentes (≈21,55 g/ml). Esto reduciría la incertidumbre relativa al hacer comparaciones de masa en el aire . Alternativamente, se podrían explorar materiales y construcciones completamente diferentes con el objetivo de producir patrones de masa con mayor estabilidad. Por ejemplo, se podrían investigar aleaciones de osmio -iridio si la propensión del platino a absorber hidrógeno (debido a la catálisis de COV y disolventes de limpieza a base de hidrocarburos) y el mercurio atmosférico resultaran ser fuentes de inestabilidad. Además, se podrían investigar recubrimientos cerámicos protectores depositados en vapor, como los nitruros , para determinar su idoneidad para aislar químicamente estas nuevas aleaciones.
El desafío con las balanzas Kibble no es sólo reducir su incertidumbre, sino también hacer que sean verdaderamente realizaciones prácticas del kilogramo. Casi todos los aspectos de las balanzas Kibble y su equipo de apoyo requieren una tecnología de vanguardia tan extraordinariamente precisa y exacta que, a diferencia de un dispositivo como un reloj atómico, pocos países optarían actualmente por financiar su funcionamiento. Por ejemplo, la balanza Kibble del NIST utilizó cuatro patrones de resistencia en 2007, cada uno de los cuales rotaba a través de la balanza Kibble cada dos a seis semanas después de ser calibrado en una parte diferente de las instalaciones de la sede del NIST en Gaithersburg, Maryland . Se descubrió que simplemente mover los patrones de resistencia por el pasillo hasta la balanza Kibble después de la calibración alteraba sus valores en 10 ppb (equivalente a 10 μg) o más. [14] La tecnología actual es insuficiente para permitir el funcionamiento estable de las balanzas Kibble entre calibraciones incluso bianuales. Cuando la nueva definición entre en vigor, es probable que inicialmente solo queden unas pocas balanzas Kibble (como máximo) operando en el mundo.
Se exploraron en distintos grados varios enfoques alternativos para redefinir el kilogramo que eran fundamentalmente diferentes de la balanza de Kibble, y algunos fueron abandonados. El proyecto Avogadro, en particular, fue importante para la decisión de redefinición de 2018 porque proporcionó una medición precisa de la constante de Planck que era consistente con el método de la balanza de Kibble e independiente de él. [15] Los enfoques alternativos incluían:

Un enfoque basado en la constante de Avogadro, conocido como el proyecto Avogadro de la Coordinación Internacional de Avogadro , definiría y delinearía el kilogramo como una esfera de átomos de silicio de 93,6 mm de diámetro . Se eligió el silicio porque ya existe una infraestructura comercial con tecnología madura para crear silicio monocristalino ultrapuro y sin defectos, el proceso Czochralski , para dar servicio a la industria de los semiconductores .
Para hacer realidad el kilogramo, se fabricaría una bola de silicio (un lingote monocristalino con forma de varilla). Su composición isotópica se mediría con un espectrómetro de masas para determinar su masa atómica relativa media. La bola se cortaría, se trituraría y se puliría en esferas. El tamaño de una esfera seleccionada se mediría mediante interferometría óptica con una incertidumbre de unos 0,3 nm en el radio, aproximadamente una sola capa atómica. El espaciado reticular preciso entre los átomos de su estructura cristalina (≈ 192 pm) se mediría utilizando un interferómetro de rayos X de barrido . Esto permite determinar su espaciado atómico con una incertidumbre de solo tres partes por mil millones. Conociendo el tamaño de la esfera, su masa atómica media y su espaciado atómico, se puede calcular el diámetro de esfera necesario con suficiente precisión y baja incertidumbre para permitir pulirla hasta una masa objetivo de un kilogramo.
Se están realizando experimentos con las esferas de silicio del Proyecto Avogadro para determinar si sus masas son más estables cuando se almacenan en vacío, en vacío parcial o a presión ambiental. Sin embargo, actualmente no existen medios técnicos para demostrar una estabilidad a largo plazo mejor que la de las IPK, porque las mediciones de masa más sensibles y precisas se realizan con balanzas de dos platos, como la balanza de banda flexible FB-2 del BIPM (véase § Enlaces externos , a continuación). Las balanzas solo pueden comparar la masa de una esfera de silicio con la de una masa de referencia. Dada la última comprensión de la falta de estabilidad de masa a largo plazo con la IPK y sus réplicas, no se conoce ningún artefacto de masa perfectamente estable con el que comparar. Las balanzas de un solo plato , que miden el peso en relación con un invariante de la naturaleza, no son precisas para la incertidumbre necesaria a largo plazo de 10 a 20 partes por mil millones. Otro problema que hay que superar es que el silicio se oxida y forma una fina capa (equivalente a 5-20 átomos de silicio de profundidad) de dióxido de silicio ( cuarzo ) y monóxido de silicio . Esta capa aumenta ligeramente la masa de la esfera, un efecto que debe tenerse en cuenta al pulir la esfera hasta su tamaño final. La oxidación no es un problema con el platino y el iridio, que son metales nobles que son aproximadamente tan catódicos como el oxígeno y, por lo tanto, no se oxidan a menos que se les convenza de que lo hagan en el laboratorio. La presencia de la fina capa de óxido en un prototipo de masa de esfera de silicio impone restricciones adicionales a los procedimientos que podrían ser adecuados para limpiarlo para evitar cambiar el espesor de la capa o la estequiometría del óxido .
Todos los enfoques basados en el silicio fijarían la constante de Avogadro, pero varían en los detalles de la definición del kilogramo. Un enfoque utilizaría silicio con sus tres isótopos naturales presentes. Aproximadamente el 7,78% del silicio comprende los dos isótopos más pesados: 29Si y 30Si . Como se describe en el § Carbono-12 a continuación, este método definiría la magnitud del kilogramo en términos de un cierto número de átomos de 12 C fijando la constante de Avogadro; la esfera de silicio sería la realización práctica . Este enfoque podría delinear con precisión la magnitud del kilogramo porque las masas de los tres nucleidos de silicio en relación con 12 C se conocen con gran precisión (incertidumbres relativas de 1 ppb o mejores). Un método alternativo para crear un kilogramo basado en una esfera de silicio propone utilizar técnicas de separación isotópica para enriquecer el silicio hasta que sea casi 28 Si puro, que tiene una masa atómica relativa de 27.976 926 5325 (19) . [16] Con este enfoque, no solo se fijaría la constante de Avogadro, sino también la masa atómica del 28 Si. Como tal, la definición del kilogramo se desvincularía de 12 C y el kilogramo se definiría en cambio como 1000/27.976 926 5325 ⋅6,022 141 79 × 10 23 átomos de 28 Si (≈35.743 740 43 moles fijos de átomos de 28 Si). Los físicos podrían optar por definir el kilogramo en términos de 28 Si incluso cuando los prototipos de kilogramo están hechos de silicio natural (los tres isótopos están presentes). Incluso con una definición de kilogramo basada en 28 Si teóricamente puro, un prototipo de esfera de silicio hecho solo de 28 Si casi puro necesariamente se desviaría ligeramente del número definido de moles de silicio para compensar varias impurezas químicas e isotópicas, así como el efecto de los óxidos de la superficie. [17] [ enlace muerto ]
Aunque no ofrece una realización práctica, esta definición definiría con precisión la magnitud del kilogramo en términos de un cierto número de átomos de carbono-12 . El carbono-12 ( 12 C) es un isótopo del carbono. El mol se define actualmente como "la cantidad de entidades (partículas elementales como átomos o moléculas) igual al número de átomos en 12 gramos de carbono-12". Por lo tanto, la definición actual del mol requiere que 1000/12 lunares ( 83+1/3 mol) de 12 C tiene una masa de exactamente un kilogramo. El número de átomos en un mol, una cantidad conocida como la constante de Avogadro , se determina experimentalmente, y la mejor estimación actual de su valor es6.022 140 76 × 10 23 entidades por mol. [18] Esta nueva definición del kilogramo propuso fijar la constante de Avogadro en exactamente6.022 14 X × 10 23 mol −1 siendo el kilogramo definido como "la masa igual a la de 1000/12×6.022 14 X × 10 23 átomos de 12 C".
La precisión del valor medido de la constante de Avogadro está limitada actualmente por la incertidumbre en el valor de la constante de Planck . Esa incertidumbre estándar relativa ha sido de 50 partes por mil millones (ppb) desde 2006. Al fijar la constante de Avogadro, el efecto práctico de esta propuesta sería que la incertidumbre en la masa de un átomo de 12 C -y la magnitud del kilogramo- no podría ser mejor que la incertidumbre actual de 50 ppb en la constante de Planck. Según esta propuesta, la magnitud del kilogramo estaría sujeta a un refinamiento futuro a medida que se disponga de mediciones mejoradas del valor de la constante de Planck; las realizaciones electrónicas del kilogramo se recalibrarían según fuera necesario. Por el contrario, una definición electrónica del kilogramo (véase § Enfoques electrónicos , más abajo), que fijaría con precisión la constante de Planck, seguiría permitiendo 83+1/3Se estima que moles de 12 C tienen una masa de exactamente un kilogramo, pero el número de átomos que componen un mol (la constante de Avogadro) seguiría estando sujeto a futuros refinamientos.
Una variación de una definición basada en 12 C propone definir la constante de Avogadro como precisamente84 446 889 3 (≈ 6,022 141 62 × 10 23 ) átomos. Una realización imaginaria de un prototipo de masa de 12 gramos sería un cubo de 12 átomos de C que midiera exactamente84 446 889 átomos de lado. Con esta propuesta, el kilogramo se definiría como "la masa igual a84 446 889 3 × 83+1/3 átomos de 12 C." [19] [Nota 3]
Otro método basado en Avogadro, la acumulación de iones , que ya no se utiliza, habría definido y delimitado el kilogramo creando con precisión nuevos prototipos de metal a demanda. Lo habría hecho acumulando iones de oro o bismuto (átomos despojados de un electrón) y contándolos midiendo la corriente eléctrica necesaria para neutralizarlos. Se eligieron el oro ( 197 Au) y el bismuto ( 209 Bi) porque se pueden manipular con seguridad y tienen las dos masas atómicas más altas entre los elementos mononucleídicos que son estables (oro) o efectivamente lo son (bismuto). [Nota 4] Véase también la Tabla de nucleidos .
Con una definición del kilogramo basada en el oro, por ejemplo, la masa atómica relativa del oro podría haberse fijado con tanta precisión196.966 5687 , del valor actual de196.966 5687 (6) . Al igual que con una definición basada en el carbono 12, la constante de Avogadro también se habría fijado. El kilogramo se habría definido entonces como "la masa igual a la de exactamente 1000/196.966 5687×6,022 141 79 × 10 23 átomos de oro" (precisamente3 057 443 620 887 933 963 384 315 átomos de oro o aproximadamente5.077 003 71 moles fijos).
En 2003, los experimentos alemanes con oro a una corriente de sóloLa incertidumbre relativa de 10 μA fue del 1,5 %. [21] Se esperaba que los experimentos posteriores con iones de bismuto y una corriente de 30 mA acumularan una masa de 30 g en seis días y tuvieran una incertidumbre relativa mejor que 1 ppm. [22] Finalmente, los métodos de acumulación de iones resultaron inadecuados. Las mediciones requirieron meses y los datos resultaron demasiado erráticos para que la técnica se considerara un reemplazo viable para el IPK en el futuro. [23]
Entre los muchos desafíos técnicos del aparato de deposición de iones estaba la obtención de una corriente de iones suficientemente alta (tasa de deposición de masa) y, al mismo tiempo, la desaceleración de los iones para que todos pudieran depositarse sobre un electrodo objetivo incrustado en un platillo de balanza. Los experimentos con oro mostraron que los iones debían desacelerarse a energías muy bajas para evitar efectos de chisporroteo , un fenómeno por el cual los iones que ya se habían contado rebotan en el electrodo objetivo o incluso desalojan átomos que ya se habían depositado. La fracción de masa depositada en los experimentos alemanes de 2003 solo se acercó mucho al 100% con energías iónicas de menos de aproximadamente1 eV (< 1 km/s para el oro). [21]
Si el kilogramo se hubiera definido como una cantidad precisa de átomos de oro o bismuto depositados con una corriente eléctrica, no sólo se tendrían que haber fijado con precisión la constante de Avogadro y la masa atómica del oro o del bismuto, sino también el valor de la carga elemental ( e ), probablemente1.602 17 X × 10 −19 C (del valor recomendado actualmente de1.602 176 634 × 10 −19 C 24] ). De esa manera se habría definido efectivamente el amperio como un flujo de 1/1.602 17 X × 10 −19 electrones por segundo que pasan por un punto fijo en un circuito eléctrico. La unidad de masa del SI se habría definido completamente si se hubieran fijado con precisión los valores de la constante de Avogadro y la carga elemental, y si se hubiera aprovechado el hecho de que las masas atómicas de los átomos de bismuto y oro son constantes invariables y universales de la naturaleza.
Además de la lentitud de la fabricación de un nuevo patrón de masa y de la escasa reproducibilidad, el método de acumulación de iones tenía otras deficiencias intrínsecas que resultaron ser obstáculos formidables para que las técnicas basadas en la acumulación de iones se convirtieran en una realización práctica. El aparato requería necesariamente que la cámara de deposición tuviera un sistema de equilibrio integrado para permitir la calibración conveniente de una cantidad razonable de patrones de transferencia en relación con cualquier prototipo interno depositado de iones. Además, los prototipos de masa producidos mediante técnicas de deposición de iones no se habrían parecido en nada a los prototipos independientes de platino-iridio que se utilizan actualmente; se habrían depositado sobre un electrodo incrustado en una de las bandejas de una balanza especial integrada en el dispositivo y se habrían convertido en parte de él. Además, la masa depositada de iones no habría tenido una superficie dura y muy pulida que se pueda limpiar enérgicamente como las de los prototipos actuales. El oro, aunque es un metal denso y noble (resistente a la oxidación y a la formación de otros compuestos), es extremadamente blando, por lo que un prototipo interno de oro debería mantenerse bien aislado y escrupulosamente limpio para evitar la contaminación y el potencial desgaste por tener que eliminar la contaminación. El bismuto, que es un metal económico que se utiliza en soldaduras de baja temperatura, se oxida lentamente cuando se expone al aire a temperatura ambiente y forma otros compuestos químicos, por lo que no habría producido masas de referencia estables a menos que se mantuviera continuamente en vacío o en una atmósfera inerte.

Este enfoque definiría el kilogramo como "la masa que se aceleraría exactamente a2 × 10 −7 m/s 2 cuando se somete a la fuerza por metro entre dos conductores rectos paralelos de longitud infinita, de sección transversal circular despreciable, colocados a un metro de distancia en el vacío, a través de los cuales fluye una corriente constante de 1/1.602 17 × 10 −19" cargas elementales por segundo".
En efecto, esto definiría al kilogramo como una derivada del amperio en lugar de la relación actual, que define al amperio como una derivada del kilogramo. Esta redefinición del kilogramo especificaría la carga elemental ( e ) exactamente como 1,602 17 × 10 −19 culombio en lugar del valor recomendado actual de1.602 176 634 × 10 −19 C . [24] Se seguiría necesariamente que el amperio (un culombio por segundo) también se convertiría en una corriente eléctrica de esta cantidad precisa de cargas elementales por segundo que pasan por un punto dado en un circuito eléctrico. La virtud de una realización práctica basada en esta definición es que a diferencia de la balanza de Kibble y otros métodos basados en escalas, todos los cuales requieren la caracterización cuidadosa de la gravedad en el laboratorio, este método delinea la magnitud del kilogramo directamente en los mismos términos que definen la naturaleza de la masa: aceleración debido a una fuerza aplicada. Desafortunadamente, es extremadamente difícil desarrollar una realización práctica basada en masas aceleradas. Los experimentos durante un período de años en Japón con una masa superconductora de 30 g sostenida por levitación diamagnética nunca lograron una incertidumbre mejor que diez partes por millón. La histéresis magnética fue uno de los problemas limitantes. Otros grupos realizaron investigaciones similares que utilizaron diferentes técnicas para levitar la masa. [25] [26]
La constante de Avogadro y la constante de Planck están entrelazadas en las leyes de la física. Tras medir la constante de Avogadro, el Dr. Bettin pudo derivar la constante de Planck. Y con una medida precisa de la constante de Planck, pudo validar los resultados del trabajo del Dr. Kibble, y viceversa.