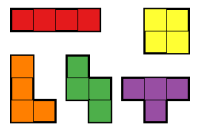
Un tetrominó es una figura geométrica compuesta por cuatro cuadrados , conectados ortogonalmente (es decir, por los bordes y no por las esquinas). [1] [2] Los tetrominós, como los dominós y los pentominós , son un tipo particular de poliominó . El policubo correspondiente , llamado tetracubo , es una figura geométrica compuesta por cuatro cubos conectados ortogonalmente.
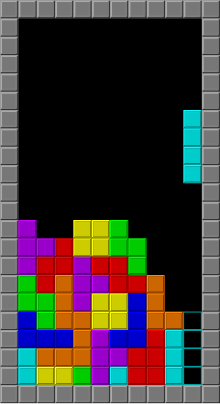
Un uso popular de los tetrominós es en el videojuego Tetris creado por el diseñador de juegos soviético Alexey Pajitnov , que se refiere a ellos como tetriminos . [3] Los tetrominós utilizados en el juego son específicamente los tetrominós de un solo lado.
Los poliominós se forman uniendo cuadrados unitarios a lo largo de sus bordes. Un poliominó libre es un poliominó considerado hasta la congruencia . Es decir, dos poliominós libres son iguales si existe una combinación de traslaciones , rotaciones y reflexiones que convierte a uno en el otro. Un tetrominó libre es un poliominó libre formado por cuatro cuadrados. Hay cinco tetrominós libres.
Los tetrominós libres tienen la siguiente simetría:
Los tetrominós unilaterales son tetrominós que pueden trasladarse y rotarse, pero no reflejarse. Se utilizan en Tetris y se asocian abrumadoramente con él. Hay siete tetrominós unilaterales distintos. Estos tetrominós se nombran por la letra del alfabeto a la que más se parecen. Los tetrominós "I", "O" y "T" tienen simetría reflexiva, por lo que no importa si se consideran tetrominós libres o tetrominós unilaterales. Los cuatro tetrominós restantes, "J", "L", "S" y "Z", exhiben un fenómeno llamado quiralidad . J y L son reflejos entre sí, y S y Z son reflejos entre sí.
Como tetrominós libres, J es equivalente a L y S es equivalente a Z, pero en dos dimensiones y sin reflexiones, no es posible transformar J en L ni S en Z.
Los tetrominós fijos sólo permiten la traslación, no la rotación ni la reflexión. Hay dos tetrominós I fijos distintos, cuatro J, cuatro L, un O, dos S, cuatro T y dos Z, lo que da un total de 19 tetrominós fijos.
Un único conjunto de tetrominós libres o tetrominós de un solo lado no puede caber en un rectángulo. Esto se puede demostrar con una prueba similar al argumento del tablero de ajedrez mutilado . Un rectángulo de 5 × 4 con un patrón de tablero de ajedrez tiene 20 cuadrados, que contienen 10 cuadrados claros y 10 cuadrados oscuros, pero un conjunto completo de tetrominós libres tiene 11 cuadrados oscuros y 9 cuadrados claros, o 11 cuadrados claros y 9 cuadrados oscuros. Esto se debe a que el tetrominó T tiene 3 cuadrados oscuros y un cuadrado claro, o 3 cuadrados claros y un cuadrado oscuro, mientras que todos los demás tetrominós tienen cada uno 2 cuadrados oscuros y 2 cuadrados claros. De manera similar, un rectángulo de 7 × 4 tiene 28 cuadrados, que contienen 14 cuadrados de cada tono, pero el conjunto de tetrominós de un solo lado tiene 15 cuadrados oscuros y 13 cuadrados claros, o 15 cuadrados claros y 13 cuadrados oscuros. Por extensión, cualquier número impar de conjuntos de cualquiera de los dos tipos no cabe en un rectángulo. Además, los 19 tetrominós fijos no caben en un rectángulo de 4×19. Esto se descubrió agotando todas las posibilidades en una búsqueda por computadora.
Otra consecuencia de que el tetrominó T tenga 3 cuadrados de un color y 1 cuadrado del otro es que cualquier rectángulo que contenga un número par de cuadrados debe contener un número par de tetrominós T. A la inversa, cualquier rectángulo que contenga un número impar de cuadrados debe contener un número impar de tetrominós T.
Los tres juegos de tetrominós pueden encajar en rectángulos con agujeros:
Dos conjuntos de tetrominós libres o de un solo lado pueden encajar en un rectángulo de diferentes maneras, como se muestra a continuación:
El nombre "tetromino" es una combinación del prefijo tetra- "cuatro" (del griego antiguo τετρα- ) y " dominó ". El nombre fue introducido por Solomon W. Golomb en 1953 junto con otra nomenclatura relacionada con los poliominos. [4] [1]
Cada uno de los cinco tetrominós libres tiene un tetracubo correspondiente, que es el tetrominó extruido en una unidad. J y L son el mismo tetracubo, al igual que S y Z, porque uno puede rotarse alrededor de un eje paralelo al plano del tetrominó para formar el otro. Son posibles tres tetracubos más, todos creados colocando un cubo unitario sobre el tricubo doblado :
Los tetracubos se pueden empaquetar en cajas tridimensionales de dos capas de varias maneras diferentes, según las dimensiones de la caja y los criterios de inclusión. Se muestran tanto en un diagrama gráfico como en un diagrama de texto. En el caso de las cajas que utilizan dos conjuntos de las mismas piezas, el diagrama gráfico representa cada conjunto con un tono más claro o más oscuro del mismo color. El diagrama de texto representa cada conjunto con una letra mayúscula o minúscula. En el diagrama de texto, la capa superior está a la izquierda y la capa inferior a la derecha.
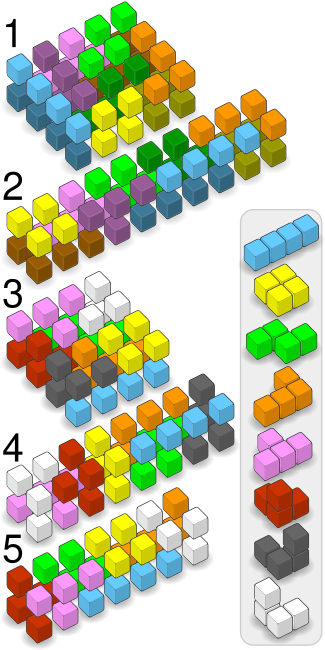
1.) Caja de 2×4×5 llena con dos juegos de tetrominós libres:ZZT t I l TTT iLZZ t y llltiL zzt yo oozziLLOOI oo OO yo2.) Caja de 2×2×10 llena con dos juegos de tetrominós libres:LLL zz ZZTOO oozz ZZTTT lLIIII ttt OO ooiiiitlll3.) Caja de 2×4×4 llena con un juego de todos los tetrominós:¡Vaya!FFTBZZBB¡VIEJOOOOOO!Dios mío4.) Caja de 2×2×8 llena con un juego de todos los tetrominós:DZZLOTTTDLLLOBFFDDZZOBTFIIIIOBBF5.) Caja de 2×2×7 llena de tetrominós, con las piezas reflejadas eliminadas:LLLZZBBLCOOZZBCIIITBCCOOTT