
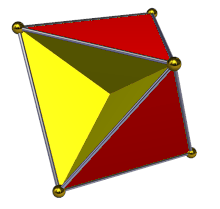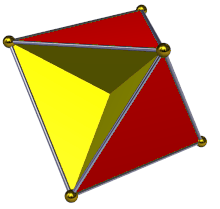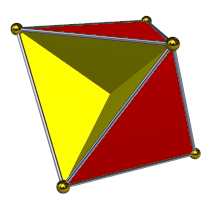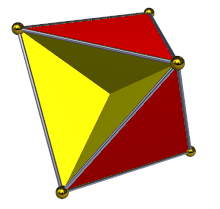

En geometría , el tetrahemihexaedro o hemicuboctaedro es un poliedro estrellado uniforme , indexado como U 4 . Tiene 7 caras (4 triángulos y 3 cuadrados ), 12 aristas y 6 vértices. [1] Su figura de vértice es un cuadrilátero cruzado . Su diagrama de Coxeter-Dynkin es![]()
![]()
![]()
![]()
![]()
![]()
![]() (aunque se trata de una doble cobertura del tetrahemihexaedro).
(aunque se trata de una doble cobertura del tetrahemihexaedro).
El tetrahemihexaedro es el único poliedro uniforme no prismático con un número impar de caras. Su símbolo de Wythoff es 3/2 3 | 2 , pero representa una doble cobertura del tetrahemihexaedro con ocho triángulos y seis cuadrados, emparejados y coincidentes en el espacio. (Puede verse más intuitivamente como dos tetrahemihexaedros coincidentes).
El tetrahemihexaedro es un hemipoliedro . La parte "hemi" del nombre significa que algunas de las caras forman un grupo con la mitad de miembros que un poliedro regular (aquí, tres caras cuadradas forman un grupo con la mitad de caras que el hexaedro regular, mejor conocido como cubo), de ahí el nombre hemihexaedro . Las caras hemi también están orientadas en la misma dirección que las caras del poliedro regular. Las tres caras cuadradas del tetrahemihexaedro son, como las tres orientaciones faciales del cubo, mutuamente perpendiculares .
La característica de "la mitad de" también significa que las semicaras deben pasar por el centro del poliedro, donde se intersecan entre sí. Visualmente, cada cuadrado se divide en cuatro triángulos rectángulos , con dos visibles desde cada lado.
El tetrahemihexaedro es una superficie no orientable . Es único por ser el único poliedro uniforme con una característica de Euler de 1 y, por lo tanto, es un poliedro proyectivo , lo que produce una representación del plano proyectivo real [2] muy similar a la superficie romana .
El tetrahemihexaedro tiene los mismos vértices y aristas que el octaedro regular . También comparte 4 de las 8 caras triangulares del octaedro, pero tiene tres caras cuadradas adicionales que pasan por el centro del poliedro.
La figura dual del tetrahemihexaedro es el tetrahemihexacrón .
El tetrahemihexaedro está 2-cubierto por el cuboctaedro [2], que por consiguiente tiene la misma figura abstracta de vértices (2 triángulos y dos cuadrados: 3.4.3.4) y el doble de vértices, aristas y caras. Tiene la misma topología que el poliedro abstracto hemi-cuboctaedro .
El tetrahemihexaedro también puede construirse como un cuploide triangular cruzado . Todos los cuploides y sus duales son planos proyectivos topológicamente. [3]
El tetrahemihexacrono es el dual del tetrahemihexaedro, y es uno de los nueve hemipoliedros duales .
Como los hemipoliedros tienen caras que pasan por el centro, las figuras duales tienen vértices correspondientes en el infinito; propiamente, en el plano proyectivo real en el infinito. [4] En los modelos duales de Magnus Wenninger , se representan con prismas que se intersecan , cada uno de los cuales se extiende en ambas direcciones hasta el mismo vértice en el infinito, para mantener la simetría. En la práctica, los prismas modelo se cortan en un punto determinado que es conveniente para el creador. Wenninger sugirió que estas figuras son miembros de una nueva clase de figuras de estelación , llamada estelación al infinito . Sin embargo, también sugirió que, estrictamente hablando, no son poliedros porque su construcción no se ajusta a las definiciones habituales.
Topológicamente, se considera que el tetrahemihexacrono contiene siete vértices. Los tres vértices considerados en el infinito (el plano proyectivo real en el infinito) corresponden direccionalmente a los tres vértices del hemioctaedro , un poliedro abstracto. Los otros cuatro vértices existen en vértices alternos de un cubo central (un semicubo , en este caso un tetraedro ).