Teorema del jurado de Condorcet

Teorema de la ciencia política

Gráfico de probabilidades acumuladas de éxito (eje y) para algunas distribuciones binomiales con una probabilidad de éxito individual determinada (eje x) y el número de “jurados” (color).

El teorema del jurado de Condorcet es un teorema de ciencia política sobre la probabilidad relativa de que un grupo determinado de individuos llegue a una decisión correcta. El teorema fue expresado por primera vez por el marqués de Condorcet en su obra de 1785 Ensayo sobre la aplicación del análisis a la probabilidad de decisiones mayoritarias . ^[1]

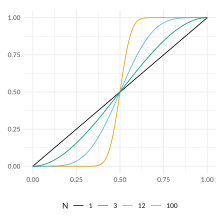
Los supuestos del teorema son que un grupo desea llegar a una decisión por mayoría de votos . Uno de los dos resultados de la votación es correcto y cada votante tiene una probabilidad independiente p de votar por la decisión correcta. El teorema pregunta cuántos votantes deberíamos incluir en el grupo. El resultado depende de si p es mayor o menor que 1/2:

• Si p es mayor que 1/2 (es más probable que cada votante vote correctamente), agregar más votantes aumenta la probabilidad de que la decisión mayoritaria sea correcta. En el límite, la probabilidad de que la mayoría vote correctamente se acerca a 1 a medida que aumenta el número de votantes.
• Por otro lado, si p es menor que 1/2 (es más probable que cada votante vote incorrectamente), entonces agregar más votantes empeora las cosas: el jurado óptimo está formado por un solo votante.

Desde Condorcet, muchos otros investigadores han demostrado varios otros teoremas del jurado , relajando algunas o todas las suposiciones de Condorcet.

Pruebas

Prueba 1: Calcular la probabilidad de que dos votantes adicionales cambien el resultado

Para evitar la necesidad de una regla de desempate, suponemos que n es impar. Esencialmente, el mismo argumento funciona incluso para n si los empates se rompen añadiendo un solo votante.

Ahora supongamos que comenzamos con n votantes y dejamos que m de estos votantes voten correctamente.

Considere lo que sucede cuando sumamos dos votantes más (para mantener el número total impar). El voto mayoritario cambia sólo en dos casos:

• m era un voto demasiado pequeño para obtener la mayoría de los n votos, pero ambos nuevos votantes votaron correctamente.
• m era igual a una mayoría de n votos, pero ambos nuevos votantes votaron incorrectamente.

El resto del tiempo, o los nuevos votos se anulan, sólo aumentan la brecha o no marcan una diferencia suficiente. Así que sólo nos importa lo que sucede cuando un solo voto (entre los primeros n ) separa una mayoría correcta de una incorrecta.

Restringiendo nuestra atención a este caso, podemos imaginar que los primeros n -1 votos se anulan y que el voto decisivo lo emite el n -ésimo votante. En este caso, la probabilidad de obtener una mayoría correcta es simplemente p . Ahora supongamos que enviamos a los dos votantes adicionales. La probabilidad de que cambien una mayoría incorrecta a una mayoría correcta es (1- p ) p ² , mientras que la probabilidad de que cambien una mayoría correcta a una mayoría incorrecta es p (1- p ) ² . La primera de estas probabilidades es mayor que la segunda si y sólo si p > 1/2, demostrando el teorema.

Prueba 2: Calcular la probabilidad de que la decisión sea correcta

Esta prueba es directa; simplemente resume las probabilidades de las mayorías. Cada término de la suma multiplica el número de combinaciones de una mayoría por la probabilidad de esa mayoría. Cada mayoría se cuenta usando una combinación , n elementos tomados k a la vez, donde n es el tamaño del jurado y k es el tamaño de la mayoría. Las probabilidades varían de 0 (= el voto siempre es incorrecto) a 1 (= siempre acierta). Cada persona decide de forma independiente, por lo que las probabilidades de sus decisiones se multiplican. La probabilidad de cada decisión correcta es p . La probabilidad de una decisión incorrecta, q , es la opuesta a p , es decir, 1 − p . La notación de potencia, es decir, es una abreviatura de x multiplicaciones de p . ${\displaystyle p^{x}}$

Las precisiones del comité o del jurado se pueden estimar fácilmente utilizando este enfoque en hojas de cálculo o programas de computadora.

Como ejemplo, tomemos el caso más simple de n = 3, p = 0,8. Necesitamos demostrar que 3 personas tienen más de 0,8 posibilidades de tener razón. En efecto:

0,8 × 0,8 × 0,8 + 0,8 × 0,8 × 0,2 + 0,8 × 0,2 × 0,8 + 0,2 × 0,8 × 0,8 = 0,896.

Asintóticas

La probabilidad de una decisión mayoritaria correcta P ( n ,  p ), cuando la probabilidad individual p es cercana a 1/2 crece linealmente en términos de p − 1/2. Para n votantes cada uno con probabilidad p de decidir correctamente y para n impares (donde no hay empates posibles):

${\displaystyle P(n,p)=1/2+c_{1}(p-1/2)+c_{3}(p-1/2)^{3}+O\left((p-1/2)^{5}\right),}$

dónde

${\displaystyle c_{1}={n \choose {\lfloor n/2\rfloor }}{\frac {\lfloor n/2\rfloor +1}{4^{\lfloor n/2\rfloor }}}={\sqrt {\frac {2n+1}{\pi }}}\left(1+{\frac {1}{16n^{2}}}+O(n^{-3})\right),}$

y la aproximación asintótica en términos de n es muy precisa. La expansión es sólo en potencias impares y . En términos simples, esto dice que cuando la decisión es difícil ( p cercana a 1/2), la ganancia por tener n votantes crece proporcionalmente a . ${\displaystyle c_{3}<0}$ ${\displaystyle {\sqrt {n}}}$

El teorema en otras disciplinas

El teorema del jurado de Condorcet se ha utilizado recientemente para conceptualizar la integración de puntuaciones cuando varios lectores médicos (radiólogos, endoscopistas, etc.) evalúan de forma independiente las imágenes para determinar la actividad de la enfermedad. Esta tarea surge en la lectura central realizada durante los ensayos clínicos y tiene similitudes con la votación. Según los autores, la aplicación del teorema puede traducir las puntuaciones de los lectores individuales en una puntuación final de una manera que sea matemáticamente sólida (al evitar el promedio de datos ordinales), matemáticamente manejable para análisis posteriores y de una manera que sea consistente con la tarea de puntuación en cuestión (basada en decisiones sobre la presencia o ausencia de características, una tarea de clasificación subjetiva) ^[2]

El teorema del jurado de Condorcet también se utiliza en el aprendizaje conjunto en el campo del aprendizaje automático . ^[3] Un método de conjunto combina las predicciones de muchos clasificadores individuales mediante votación mayoritaria. Suponiendo que cada uno de los clasificadores individuales predice con una precisión ligeramente superior al 50% y que sus predicciones son independientes, entonces el conjunto de sus predicciones será mucho mayor que sus puntuaciones predictivas individuales.

Aplicabilidad a los procesos democráticos

Muchos teóricos políticos y filósofos utilizan el Teorema del Jurado de Condorcet (CJT) para defender la democracia, ver Brennan ^[4] y las referencias allí contenidas. Sin embargo, es una cuestión empírica si el teorema se cumple o no en la vida real. Tenga en cuenta que el CJT es un arma de doble filo : puede demostrar que la regla de la mayoría es un mecanismo (casi) perfecto para agregar información, cuando , o un desastre (casi) perfecto, cuando . Un desastre significaría que se elige sistemáticamente la opción equivocada. Algunos autores han sostenido que nos encontramos en este último escenario. Por ejemplo, Bryan Caplan ha argumentado extensamente que el conocimiento de los votantes está sistemáticamente sesgado hacia opciones (probablemente) incorrectas. En la configuración del CJT, esto podría interpretarse como evidencia de . ${\displaystyle p>1/2}$ ${\displaystyle p<1/2}$ ${\displaystyle p<1/2}$

Recientemente, se adoptó otro enfoque para estudiar la aplicabilidad del CJT. ^[5] En lugar de considerar el caso homogéneo, a cada votante se le permite tener una probabilidad , posiblemente diferente de la de otros votantes. Este caso fue estudiado previamente por Daniel Berend y Jacob Paroush ^[6] e incluye el teorema clásico de Condorcet (cuando ) y otros resultados, como el Milagro de la Agregación (cuando para la mayoría de los votantes y para una pequeña proporción de ellos). Luego, siguiendo un enfoque bayesiano, se estima la probabilidad previa (en este caso, a priori ) de la tesis predicha por el teorema. Es decir, si elegimos una secuencia arbitraria de votantes (es decir, una secuencia ), ¿se mantendrá la tesis del CJT? La respuesta es no. Más precisamente, si se toma una secuencia aleatoria de siguiendo una distribución insesgada que no favorece la competencia, o la incompetencia, entonces la tesis predicha por el teorema no se cumplirá casi con seguridad . Con este nuevo enfoque, los defensores del CJT deberían presentar pruebas sólidas de competencia para superar la baja probabilidad anterior. Es decir, no se trata sólo de que exista evidencia en contra de la competencia (probabilidad posterior), sino también de que no podemos esperar que el CJT se mantenga en ausencia de cualquier evidencia (probabilidad previa). ${\displaystyle p_{i}\in [0,1]}$ ${\displaystyle p_{i}=p~~\forall ~i\in \mathbb {N} }$ ${\displaystyle p_{i}=1/2}$ ${\displaystyle p_{i}=1}$ ${\displaystyle (p_{i})_{i\in \mathbb {N} }}$ ${\displaystyle p_{i}}$ ${\displaystyle p_{i}>1/2}$ ${\displaystyle p_{i}<1/2}$

Otras lecturas

• método condorcet
• Paradoja de Condorcet
• teorema del jurado
• Ley de los grandes números
• Sabiduría de la multitud

Notas

1. Marqués de Condorcet (1785). Essai sur l'application de l'analyse à la probabilité des décisions rendues à la pluralité des voix (PNG) (en francés) . Consultado el 10 de marzo de 2008 .
2. Gottlieb, Klaus; Hussain, Fez (19 de febrero de 2015). "Votación por evaluación y puntuación de imágenes (VISA): teoría y aplicación de un algoritmo de lector 2 + 1 para mejorar la precisión de los criterios de valoración de imágenes en ensayos clínicos". BMC Imágenes Médicas . 15 : 6. doi : 10.1186/s12880-015-0049-0 . ISSN  1471-2342. PMC 4349725 . PMID  25880066. 
3. "Bosque aleatorio". mlu-explain.github.io . Consultado el 24 de mayo de 2022 .
4. Brennan, Jason (2011). "Teorema del jurado de Condorcet y número óptimo de votantes". Política . 31 (2): 55–62. doi :10.1111/j.1467-9256.2011.01403.x. ISSN  0263-3957. S2CID  152938266.
5. Romaniega Sancho, Álvaro (2022). "Sobre la probabilidad del teorema del jurado de Condorcet o el milagro de la agregación". Ciencias Sociales Matemáticas . 119 : 41–55. arXiv : 2108.00733 . doi :10.1016/j.mathsocsci.2022.06.002. S2CID  249921504.
6. Berend, Daniel; Paroush, Jacob (1998). "¿Cuándo es válido el teorema del jurado de Condorcet?". Elección social y bienestar . 15 (4): 481–488. doi :10.1007/s003550050118. ISSN  0176-1714. JSTOR  41106274. S2CID  120012958.