Error absoluto medio

Medida de error estadístico

En estadística , el error absoluto medio ( EMA ) es una medida de errores entre observaciones pareadas que expresan el mismo fenómeno. Los ejemplos de Y versus X incluyen comparaciones de lo predicho versus lo observado, el tiempo posterior versus el tiempo inicial y una técnica de medición versus una técnica de medición alternativa. El EMA se calcula como la suma de los errores absolutos (es decir, la distancia de Manhattan ) dividida por el tamaño de la muestra : ^[1] Por lo tanto, es un promedio aritmético de los errores absolutos , donde es la predicción y el valor verdadero. Las formulaciones alternativas pueden incluir frecuencias relativas como factores de peso. El error absoluto medio usa la misma escala que los datos que se miden. Esto se conoce como una medida de precisión dependiente de la escala y, por lo tanto, no se puede usar para hacer comparaciones entre valores predichos que usan diferentes escalas. ^[2] El error absoluto medio es una medida común del error de pronóstico en el análisis de series de tiempo , ^[3] a veces se usa en confusión con la definición más estándar de desviación absoluta media . La misma confusión existe de manera más general. $${\displaystyle \mathrm {MAE} ={\frac {\sum _{i=1}^{n}\left|y_{i}-x_{i}\right|}{n}}={\frac {\sum _{i=1}^{n}\left|e_{i}\right|}{n}}.}$$ ${\displaystyle |e_{i}|=|y_{i}-x_{i}|}$ ${\displaystyle y_{i}}$ ${\displaystyle x_{i}}$

Desacuerdos sobre cantidad y desacuerdos sobre asignación

Dos puntos de datos para los cuales el desacuerdo de cantidad es 0 y el desacuerdo de asignación es 2 tanto para MAE como para RMSE.

En teledetección, el error medio de medición se expresa a veces como la suma de dos componentes: el desacuerdo cuantitativo y el desacuerdo en la asignación. El desacuerdo cuantitativo es el valor absoluto del error medio: ^[4] El desacuerdo en la asignación es el error medio de medición menos el desacuerdo cuantitativo. $${\displaystyle \left|{\frac {\sum _{i=1}^{n}y_{i}-x_{i}}{n}}\right|.}$$

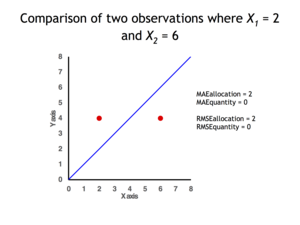
También es posible identificar los tipos de diferencias observando un gráfico. Existe una diferencia de cantidad cuando el promedio de los valores X no es igual al promedio de los valores Y. Existe una diferencia de asignación si y solo si los puntos se encuentran en ambos lados de la línea de identidad. ^{[4] [5]} ${\displaystyle (x,y)}$

Medidas relacionadas

El error absoluto medio es una de las diversas formas de comparar los pronósticos con sus resultados finales. Las alternativas bien establecidas son el error absoluto medio escalado (MASE), el error absoluto medio logarítmico (MALE) y el error cuadrático medio . Todos ellos resumen el desempeño de maneras que no tienen en cuenta la dirección de la predicción excesiva o insuficiente; una medida que sí pone énfasis en esto es la diferencia media con signo .

Cuando se debe ajustar un modelo de predicción utilizando una medida de rendimiento seleccionada, en el sentido de que el enfoque de mínimos cuadrados está relacionado con el error cuadrático medio , el equivalente del error absoluto medio son las desviaciones absolutas mínimas .

El error cuadrático medio (MAE) no es idéntico al error cuadrático medio (RMSE), aunque algunos investigadores lo informan e interpretan de esa manera. El MAE es conceptualmente más simple y también más fácil de interpretar que el RMSE: es simplemente la distancia vertical u horizontal absoluta promedio entre cada punto en un diagrama de dispersión y la línea Y=X. En otras palabras, el MAE es la diferencia absoluta promedio entre X e Y. Además, cada error contribuye al MAE en proporción al valor absoluto del error. Esto es en contraste con el RMSE, que implica elevar al cuadrado las diferencias, de modo que unas pocas diferencias grandes aumentarán el RMSE en mayor grado que el MAE. ^[4]

Propiedad de optimalidad

El error absoluto medio de una variable real c con respecto a la variable aleatoria  X es Siempre que la distribución de probabilidad de X sea tal que exista la expectativa anterior, entonces m es una mediana de X si y solo si m es un minimizador del error absoluto medio con respecto a X. ^[6] En particular, m es una mediana de muestra si y solo si m minimiza la media aritmética de las desviaciones absolutas. ^[7] $${\displaystyle E(\left|X-c\right|).}$$

En términos más generales, una mediana se define como un mínimo de, como se explica en Mediana multivariante (y específicamente en Mediana espacial ). Esta definición de la mediana basada en la optimización es útil en el análisis de datos estadísticos, por ejemplo, en la agrupación de k -medianas . $${\displaystyle E(|X-c|-|X|),}$$

Prueba de optimalidad

Afirmación: El clasificador que minimiza es . ${\displaystyle \mathbb {E} |y-{\hat {y}}|}$ ${\displaystyle {\hat {f}}(x)={\text{Median}}(y|X=x)}$

Prueba:

Las funciones de pérdida para la clasificación son Diferenciar con respecto a da Esto significa Por lo tanto, $${\displaystyle {\begin{aligned}L&=\mathbb {E} [|y-a||X=x]\\&=\int _{-\infty }^{\infty }|y-a|f_{Y|X}(y)\,dy\\&=\int _{-\infty }^{a}(a-y)f_{Y|X}(y)\,dy+\int _{a}^{\infty }(y-a)f_{Y|X}(y)\,dy.\\\end{aligned}}}$$ $${\displaystyle {\frac {\partial }{\partial a}}L=\int _{-\infty }^{a}f_{Y|X}(y)\,dy+\int _{a}^{\infty }-f_{Y|X}(y)\,dy=0.}$$ $${\displaystyle \int _{-\infty }^{a}f(y)\,dy=\int _{a}^{\infty }f(y)\,dy.}$$ $${\displaystyle F_{Y|X}(a)=0.5.}$$

Véase también

• Desviaciones absolutas mínimas
• Distancia de Manhattan
• Error porcentual absoluto medio
• Error porcentual medio
• Error porcentual absoluto medio simétrico

Referencias

1. Willmott, Cort J.; Matsuura, Kenji (19 de diciembre de 2005). "Ventajas del error absoluto medio (MAE) sobre el error cuadrático medio (RMSE) en la evaluación del rendimiento promedio del modelo". Climate Research . 30 : 79–82. doi : 10.3354/cr030079 .
2. "2.5 Evaluación de la precisión de las previsiones | OTexts". www.otexts.org . Consultado el 18 de mayo de 2016 .
3. Hyndman, R. y Koehler A. (2005). "Otra mirada a las medidas de precisión de los pronósticos" [1]
4. Pontius Jr., Robert Gilmore; Thontteh, Olufunmilayo; Chen, Hao (2008). "Componentes de información para la comparación de resolución múltiple entre mapas que comparten una variable real" (PDF) . Estadísticas ambientales y ecológicas . 15 (2): 111–142. doi :10.1007/s10651-007-0043-y. S2CID  21427573.
5. Willmott, CJ; Matsuura, K. (enero de 2006). "Sobre el uso de medidas de error dimensionadas para evaluar el rendimiento de los interpoladores espaciales". Revista Internacional de Ciencias de la Información Geográfica . 20 : 89–102. doi :10.1080/13658810500286976. S2CID  15407960.
6. Stroock, Daniel (2011). Probability Theory . Cambridge University Press. pp. 43. ISBN 978-0-521-13250-3.
7. DeGroot, Morris H. (1970). Decisiones estadísticas óptimas. McGraw-Hill Book Co., Nueva York-Londres-Sydney. pág. 232. ISBN 9780471680291.Sr. 0356303  .