

La proyección estereográfica , también conocida como proyección planisferica o proyección conforme azimutal , es una proyección cartográfica conforme cuyo uso se remonta a la antigüedad. Al igual que la proyección ortográfica y la proyección gnomónica , la proyección estereográfica es una proyección azimutal y, cuando se realiza sobre una esfera, también una proyección en perspectiva .
En un elipsoide , la definición de perspectiva de la proyección estereográfica no es conforme, y se deben realizar ajustes para preservar sus propiedades azimutales y conformes. El sistema de coordenadas estereográficas polares universales utiliza una implementación elipsoidal de este tipo.

La proyección estereográfica era probablemente conocida en su aspecto polar por los antiguos egipcios , aunque su invención se atribuye a menudo a Hiparco , que fue el primer griego en utilizarla. [ cita requerida ] Su aspecto oblicuo fue utilizado por el matemático griego Teón de Alejandría en el siglo IV, y su aspecto ecuatorial fue utilizado por el astrónomo árabe Al-Zarkali en el siglo XI. La primera descripción escrita de la misma es el Planisphaerium de Ptolomeo , que la llama "proyección del planisferio".
La proyección estereográfica se utilizó exclusivamente para mapas estelares hasta 1507, cuando Walther Ludd de Saint-Dié, Lorraine, creó el primer ejemplo conocido de una proyección estereográfica de la superficie de la Tierra. Su popularidad en cartografía aumentó después de que Rumold Mercator utilizara su aspecto ecuatorial para su atlas de 1595. [1] Posteriormente, se utilizó con frecuencia a lo largo del siglo XVII, y su aspecto ecuatorial se utilizó para mapas de los hemisferios oriental y occidental . [2]
En 1695, Edmond Halley , motivado por su interés en los mapas estelares , publicó la primera prueba matemática de que este mapa es conforme . [3] Utilizó las herramientas recientemente establecidas del cálculo , inventadas por su amigo Isaac Newton .
La forma esférica de la proyección estereográfica se expresa habitualmente en coordenadas polares:
donde es el radio de la esfera, y y son la latitud y longitud, respectivamente.
La esfera se suele elegir para modelar la Tierra cuando la extensión de la región mapeada supera unos pocos cientos de kilómetros de longitud en ambas dimensiones. Para mapas de regiones más pequeñas, se debe elegir un modelo elipsoidal si se requiere mayor precisión. [1]
La forma elipsoidal de la proyección elipsoidal polar utiliza la latitud conforme . Existen varias formas de proyecciones estereográficas transversales u oblicuas de elipsoides. Un método utiliza la proyección doble a través de una esfera conforme, mientras que otros métodos no lo hacen.
Ejemplos de proyecciones estereográficas transversales u oblicuas incluyen la proyección estereográfica oblada de Miller [4] y la proyección estereográfica oblicua de Roussilhe . [2]
Como proyección acimutal, la proyección estereográfica representa fielmente las direcciones relativas de todos los círculos mayores que pasan por su punto central. Como proyección conforme, representa fielmente los ángulos en todas partes. Además, en su forma esférica, la proyección estereográfica es la única proyección cartográfica que convierte todos los círculos pequeños en círculos.
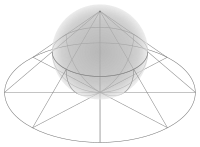
La forma esférica de la proyección estereográfica es equivalente a una proyección en perspectiva donde el punto de perspectiva está en el punto del globo opuesto al punto central del mapa.
Como la expresión para diverge cuando se aproxima a , la proyección estereográfica es infinitamente grande y es imposible mostrar el Polo Sur (para un mapa centrado en el Polo Norte). Sin embargo, es posible mostrar puntos arbitrariamente cercanos al Polo Sur siempre que los límites del mapa se extiendan lo suficiente. [1]
Los paralelos en la proyección estereográfica de Gall se distribuyen con el mismo espaciamiento que los del meridiano central de la proyección estereográfica transversal .
La proyección GS50 se forma asignando la proyección estereográfica oblicua al plano complejo y luego transformando puntos en él a través de un polinomio de décimo orden.