Bicondicional lógico

Concepto en lógica y matemáticas

Diagrama de Venn de (parte verdadera en rojo) ${\displaystyle P\leftrightarrow Q}$

En lógica y matemáticas , el bicondicional lógico , también conocido como bicondicional material o equivalencia o biimplicación o bienaventuranza , es el conectivo lógico utilizado para unir dos enunciados y formar el enunciado " si y sólo si " (a menudo abreviado como " si y sólo si " [ 1 ^] ), donde se conoce como antecedente y consecuente . ^{[2] [3]} ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle P}$ ${\displaystyle Q}$

Hoy en día, las notaciones para representar equivalencia incluyen . ${\displaystyle \leftrightarrow ,\Leftrightarrow ,\equiv }$

${\displaystyle P\leftrightarrow Q}$es lógicamente equivalente tanto a y como al operador booleano XNOR (nor exclusivo) , que significa "ambos o ninguno". ${\displaystyle (P\rightarrow Q)\land (Q\rightarrow P)}$ ${\displaystyle (P\land Q)\lor (\neg P\land \neg Q)}$

Semánticamente, el único caso en el que un bicondicional lógico es diferente de un condicional material es cuando la hipótesis (antecedente) es falsa pero la conclusión (consecuente) es verdadera. En este caso, el resultado es verdadero para el condicional, pero falso para el bicondicional. ^[2]

En la interpretación conceptual, P = Q significa "Todos los P son Q y todos los Q son P ". En otras palabras, los conjuntos P y Q coinciden: son idénticos. Sin embargo, esto no significa que P y Q deban tener el mismo significado (por ejemplo, P podría ser "triángulo equilátero" y Q podría ser "triángulo equilátero"). Cuando se formula como una oración, el antecedente es el sujeto y el consecuente es el predicado de una proposición afirmativa universal (por ejemplo, en la frase "todos los hombres son mortales", "hombres" es el sujeto y "mortal" es el predicado).

En la interpretación proposicional, significa que P implica Q y Q implica P ; en otras palabras, las proposiciones son lógicamente equivalentes , en el sentido de que ambas son o bien conjuntamente verdaderas o bien conjuntamente falsas. De nuevo, esto no significa que deban tener el mismo significado, ya que P podría ser "el triángulo ABC tiene dos lados iguales" y Q podría ser "el triángulo ABC tiene dos ángulos iguales". En general, el antecedente es la premisa , o la causa , y el consecuente es la consecuencia . Cuando una implicación se traduce por un juicio hipotético (o condicional ), el antecedente se llama hipótesis (o condición ) y el consecuente se llama tesis . ${\displaystyle P\leftrightarrow Q}$

Una forma común de demostrar un bicondicional de la forma es demostrar que y por separado (debido a su equivalencia con la conjunción de los dos condicionales inversos ^[2] ). Otra forma de demostrar el mismo bicondicional es demostrar que y . ${\displaystyle P\leftrightarrow Q}$ ${\displaystyle P\rightarrow Q}$ ${\displaystyle Q\rightarrow P}$ ${\displaystyle P\rightarrow Q}$ ${\displaystyle \neg P\rightarrow \neg Q}$

Cuando ambos miembros del bicondicional son proposiciones, se puede separar en dos condicionales, de los cuales uno se llama teorema y el otro su recíproco . ^{[ cita requerida ]} Así, siempre que un teorema y su recíproco sean verdaderos, tenemos un bicondicional. Un teorema simple da lugar a una implicación, cuyo antecedente es la hipótesis y cuyo consecuente es la tesis del teorema.

Se dice a menudo que la hipótesis es condición suficiente de la tesis, y que la tesis es condición necesaria de la hipótesis. Es decir, basta con que la hipótesis sea verdadera para que la tesis sea verdadera, mientras que es necesario que la tesis sea verdadera si la hipótesis fuera verdadera. Cuando un teorema y su recíproco son verdaderos, se dice que su hipótesis es condición necesaria y suficiente de la tesis. Es decir, la hipótesis es a la vez causa y consecuencia de la tesis.

Notaciones

Las notaciones para representar la equivalencia utilizadas en la historia incluyen:

• ${\displaystyle =}$en George Boole en 1847. ^[4] Aunque Boole utilizó principalmente en clases, también consideró el caso de que sean proposiciones en , y en ese momento es equivalencia. ${\displaystyle =}$ ${\displaystyle x,y}$ ${\displaystyle x=y}$ ${\displaystyle =}$
• ${\displaystyle \equiv }$en Frege en 1879; ^[5]
• ${\displaystyle \sim }$en Bernays en 1918; ^[6]
• ${\displaystyle \rightleftarrows }$en Hilbert en 1927 (mientras lo utilizaba como símbolo principal en el artículo); ^[7] ${\displaystyle \sim }$
• ${\displaystyle \leftrightarrow }$en Hilbert y Ackermann en 1928 ^[8] (ellos también lo introdujeron mientras que lo usan como símbolo principal en todo el libro; es adoptado por muchos seguidores como Becker en 1933 ^[9] ); ${\displaystyle \rightleftarrows ,\sim }$ ${\displaystyle \sim }$ ${\displaystyle \leftrightarrow }$
• ${\displaystyle E}$(prefijo) en Łukasiewicz en 1929 ^[10] y (prefijo) en Łukasiewicz en 1951; ^[11] ${\displaystyle Q}$
• ${\displaystyle \supset \subset }$en Heyting en 1930; ^[12]
• ${\displaystyle \Leftrightarrow }$en Bourbaki en 1954; ^[13]
• ${\displaystyle \subset \supset }$en Chazal en 1996; ^[14]

y así sucesivamente. Alguien más también usa o ocasionalmente. ^{[ cita requerida ] [ vago ] [ aclaración necesaria ]} ${\displaystyle \operatorname {EQ} }$ ${\displaystyle \operatorname {EQV} }$

Definición

La igualdad lógica (también conocida como bicondicional) es una operación sobre dos valores lógicos , típicamente los valores de dos proposiciones , que produce un valor verdadero si y solo si ambos operandos son falsos o ambos operandos son verdaderos. ^[2]

Tabla de verdad

La siguiente es una tabla de verdad para : ${\displaystyle A\leftrightarrow B}$

Cuando hay más de dos enunciados implicados, combinarlos puede ser ambiguo. Por ejemplo, el enunciado ${\displaystyle \leftrightarrow }$

${\displaystyle x_{1}\leftrightarrow x_{2}\leftrightarrow x_{3}\leftrightarrow \cdots \leftrightarrow x_{n}}$

puede interpretarse como

${\displaystyle (((x_{1}\leftrightarrow x_{2})\leftrightarrow x_{3})\leftrightarrow \cdots )\leftrightarrow x_{n}}$,

o puede interpretarse como que todas las x _i son conjuntamente verdaderas o conjuntamente falsas :

${\displaystyle (x_{1}\land \cdots \land x_{n})\lor (\neg x_{1}\land \cdots \land \neg x_{n})}$

Resulta que estas dos afirmaciones solo son iguales cuando hay cero o dos argumentos involucrados. De hecho, las siguientes tablas de verdad solo muestran el mismo patrón de bits en la línea sin argumentos y en las líneas con dos argumentos:

${\displaystyle ~x_{1}\leftrightarrow \cdots \leftrightarrow x_{n}}$
se entiende como equivalente al diagrama de Venn central que se muestra a continuación, y la línea (ABC) en esta matriz representa la misma operación.
${\displaystyle \neg ~(\neg x_{1}\oplus \cdots \oplus \neg x_{n})}$

${\displaystyle ~x_{1}\leftrightarrow \cdots \leftrightarrow x_{n}}$
pensado como una abreviatura del diagrama de Venn directamente debajo, y la línea (ABC) en esta matriz representa la misma operación.
${\displaystyle (~x_{1}\land \cdots \land x_{n}~)}$
${\displaystyle \lor ~(\neg x_{1}\land \cdots \land \neg x_{n})}$

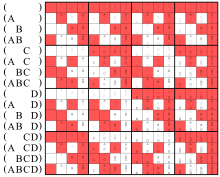
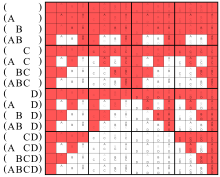
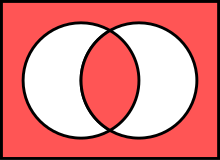
El diagrama de Venn de la izquierda a continuación y las líneas (AB) en estas matrices representan la misma operación.

Diagramas de Venn

Las áreas rojas representan valores verdaderos (como enpara y ).

Propiedades

Conmutatividad : Sí

Asociatividad : Sí

Distributividad : El bicondicional no se distribuye sobre ninguna función binaria (ni siquiera sobre sí mismo), pero la disyunción lógica se distribuye sobre el bicondicional.

Idempotencia : No

Monotonía : No

Preservación de la verdad: Sí
Cuando todas las entradas son verdaderas, la salida es verdadera.

Preservación de falsedad: No
Cuando todas las entradas son falsas, la salida no es falsa.

Espectro de Walsh : (2,0,0,2)

No linealidad : 0 (la función es lineal)

Reglas de inferencia

Como todos los conectivos en la lógica de primer orden, el bicondicional tiene reglas de inferencia que rigen su uso en pruebas formales.

Introducción bicondicional

La introducción bicondicional permite inferir que si B se sigue de A y A se sigue de B, entonces A si y sólo si B.

Por ejemplo, de las afirmaciones “si estoy respirando, entonces estoy vivo” y “si estoy vivo, entonces estoy respirando”, se puede inferir que “estoy respirando si y solo si estoy vivo” o, equivalentemente, “estoy vivo si y solo si estoy respirando”. O más esquemáticamente:

B → A    A → B    ∴ A ↔ B

B → A    A → B    ∴ B ↔ A

Eliminación bicondicional

La eliminación bicondicional permite inferir un condicional a partir de un bicondicional: si A ↔ B es verdadero, entonces se puede inferir A → B o B → A.

Por ejemplo, si es cierto que estoy respirando si y sólo si estoy vivo, entonces es cierto que si estoy respirando, entonces estoy vivo; de la misma manera, es cierto que si estoy vivo, entonces estoy respirando. O dicho de manera más esquemática:

 A ↔ B   ∴ A → B

 A ↔ B   ∴ B → A

Uso coloquial

Una forma inequívoca de enunciar un bicondicional en un lenguaje sencillo es adoptar la forma " b si a y a si b ", si no se utiliza la forma estándar " a si y sólo si b ". De forma un poco más formal, también se podría decir que " b implica a y a implica b ", o " a es necesario y suficiente para b ". El "si" del lenguaje sencillo puede utilizarse a veces como bicondicional (especialmente en el contexto de una definición matemática ^[15] ). En ese caso, hay que tener en cuenta el contexto circundante al interpretar estas palabras.

Por ejemplo, la afirmación "Te compraré una billetera nueva si la necesitas" puede interpretarse como un bicondicional, ya que el hablante no pretende que un resultado válido sea comprar la billetera independientemente de si la billetera es necesaria o no (como en un condicional). Sin embargo, "está nublado si llueve" generalmente no se entiende como un bicondicional, ya que puede estar nublado incluso si no llueve.

Véase también

• Portal de filosofía
• Portal de psicología

• Si y sólo si
• Equivalencia lógica
• Igualdad lógica
• Puerta XNOR
• Eliminación bicondicional
• Introducción bicondicional

Referencias

1. Weisstein, Eric W. "Iff". mathworld.wolfram.com . Consultado el 25 de noviembre de 2019 .
2. Peil, Timothy. "Condicionales y bicondicionales". web.mnstate.edu . Archivado desde el original el 24 de octubre de 2020 . Consultado el 25 de noviembre de 2019 .
3. Brennan, Joseph G. (1961). Manual de lógica (2.ª ed.). Harper & Row. pág. 81.
4. Boole, G. (1847). El análisis matemático de la lógica, un ensayo para el cálculo del razonamiento deductivo. Cambridge/Londres: Macmillan, Barclay y Macmillan/George Bell. pág. 17.
5. Frege, G. (1879). Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens (en alemán). Halle a/S.: Verlag von Louis Nebert. pag. 15.
6. Bernays, P. (1918). Beiträge zur axiomatischen Behandlung des Logik-Kalküls . Gotinga: Universität Göttingen. pag. 3.
7. Hilbert, D. (1928) [1927]. "Die Grundlagen der Mathematik". Abhandlungen aus dem mathematischen Seminar der Hamburgischen Universität (en alemán). 6 : 65–85. doi :10.1007/BF02940602.
8. Hilbert, D.; Ackermann, W. (1928). Grundzügen der theoretischen Logik (en alemán) (1 ed.). Berlín: Verlag von Julius Springer. pag. 4.
9. Becker, A. (1933). Die Aristotelische Theorie der Möglichkeitsschlösse: Eine logisch-philologische Untersuchung der Kapitel 13-22 von Analytica priora I de Aristóteles (en alemán). Berlín: Junker und Dünnhaupt Verlag. pag. 4.
10. Łukasiewicz, J. (1958) [1929]. Słupecki, J. (ed.). Elementy logiki matematycznej (en polaco) (2 ed.). Varsovia: Państwowe Wydawnictwo Naukowe.
11. Łukasiewicz, J. (1957) [1951]. Słupecki, J. (ed.). La silogística de Aristóteles desde el punto de vista de la lógica formal moderna (en polaco) (2.ª ed.). Glasgow, Nueva York, Toronto, Melbourne, Wellington, Bombay, Calcuta, Madrás, Karachi, Lahore, Dacca, Ciudad del Cabo, Salisbury, Nairobi, Ibadan, Accra, Kuala Lumpur y Hong Kong: Oxford University Press.
12. Heyting, A. (1930). "Die formalen Regeln der intuitionistischen Logik". Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse (en alemán): 42–56.
13. Bourbaki, N. (1954). Théorie des ensembles (en francés). París: Hermann & Cie, Éditeurs. pag. 32.
14. Chazal, G. (1996). Elementos de lógica formal . París: Publicaciones científicas de Hermes.
15. De hecho, éste es el estilo adoptado por el manual de estilo en matemáticas de Wikipedia .

Enlaces externos

• Medios relacionados con Bicondicional lógico en Wikimedia Commons

Este artículo incorpora material de Biconditional en PlanetMath , que está licenciado bajo la Licencia Creative Commons Atribución/Compartir-Igual .