función iterada

Result of repeatedly applying a mathematical function

Transformaciones iteradas del objeto de la izquierda.
En la parte superior hay una rotación de 90° en el sentido de las agujas del reloj. Tiene orden 4, porque ese es el exponente positivo más pequeño que produce la identidad. A continuación se muestra un mapeo de corte con orden infinito.
Debajo están sus composiciones , ambas de orden 3.

En matemáticas , una función iterada es una función que se obtiene componiendo otra función consigo misma dos o varias veces. El proceso de aplicar repetidamente la misma función se llama iteración . En este proceso, a partir de algún objeto inicial, el resultado de aplicar una función determinada se introduce nuevamente en la función como entrada y este proceso se repite.

Por ejemplo, en la imagen de la derecha:

${\displaystyle L=F(K),\ M=F\circ F(K)=F^{2}(K).}$

Las funciones iteradas se estudian en informática , fractales , sistemas dinámicos , matemáticas y física de grupos de renormalización .

Definición

A continuación se presenta la definición formal de una función iterada en un conjunto X.

Sea X un conjunto y f : X → X una función .

Definir f ⁿ como la n -ésima iteración de f (una notación introducida por Hans Heinrich Bürmann ^{[ cita necesaria ]} y John Frederick William Herschel ^{[1] [2] [3] [4]} ), donde n es un entero no negativo , por:

$${\displaystyle f^{0}~{\stackrel {\mathrm {def} }{=}}~\operatorname {id} _{X}}$$

$${\displaystyle f^{n+1}~{\stackrel {\mathrm {def} }{=}}~f\circ f^{n},}$$

donde id _X es la función identidad en X y ( f g )( x ) = f ( g ( x )) ${\displaystyle \circ }$ denota la composición de la función .

Debido a que la notación f ⁿ puede referirse tanto a la iteración (composición) de la función f como a la exponenciación de la función f (esta última se usa comúnmente en trigonometría ), algunos matemáticos ^{[ cita necesaria ]} optan por usar ∘ para denotar el significado compositivo, escribiendo f ^{∘ n} ( x ) para la n -ésima iteración de la función f ( x ) , como en, por ejemplo, f ^∘3 ( x ) que significa f ( f ( f ( x ))) . Con el mismo propósito, Benjamin Peirce ^{[5] [4] [nb 1]} utilizó f ^{[ n ]} ( x ) , mientras que Alfred Pringsheim y Jules Molk sugirieron ⁿ f ( x ) en su lugar. ^{[6] [4] [nota 2]}

Propiedad abeliana y secuencias de iteración.

En general, la siguiente identidad es válida para todos los números enteros no negativos m y n ,

${\displaystyle f^{m}\circ f^{n}=f^{n}\circ f^{m}=f^{m+n}~.}$

Esto es estructuralmente idéntico a la propiedad de la exponenciación de que a ^m a ⁿ = a ^{m + n} .

En general, para índices generales arbitrarios (negativos, no enteros, etc.) m y n , esta relación se denomina ecuación funcional de traducción , cf. Ecuación de Schröder y ecuación de Abel . En una escala logarítmica, esto se reduce a la propiedad de anidamiento de los polinomios de Chebyshev , T _m ( T _n ( x )) = T _{m n} ( x ) , ya que T _n ( x ) = cos ( n arccos ( x )) .

La relación ( f ^m ) ⁿ ( x ) = ( f ⁿ ) ^m ( x ) = f ^mn ( x ) también se cumple, análoga a la propiedad de la exponenciación de que ( a ^m ) ⁿ = ( a ⁿ ) ^m = a ^mn .

La secuencia de funciones f ⁿ se llama secuencia de Picard , ^{[7] [8]} que lleva el nombre de Charles Émile Picard .

Para una x dada en X , la secuencia de valores f ⁿ ( x ) se llama órbita de x .

Si f ⁿ ( x ) = f ^{n + m} ( x ) para algún número entero m > 0 , la órbita se llama órbita periódica . El valor más pequeño de m para una x dada se llama período de la órbita . El propio punto x se llama punto periódico . El problema de detección de ciclos en informática es el problema algorítmico de encontrar el primer punto periódico de una órbita y el período de la órbita.

Puntos fijos

Si x = f ( x ) para algún x en X (es decir, el período de la órbita de x es 1 ), entonces x se llama punto fijo de la secuencia iterada. El conjunto de puntos fijos suele denominarse Fix ( f ) . Existen varios teoremas del punto fijo que garantizan la existencia de puntos fijos en diversas situaciones, incluido el teorema del punto fijo de Banach y el teorema del punto fijo de Brouwer .

Existen varias técnicas para la aceleración de la convergencia de las secuencias producidas por iteración de punto fijo . ^[9] Por ejemplo, el método de Aitken aplicado a un punto fijo iterado se conoce como método de Steffensen y produce convergencia cuadrática.

Comportamiento limitante

Tras la iteración, se puede encontrar que hay conjuntos que se reducen y convergen hacia un solo punto. En tal caso, el punto al que converge se conoce como punto fijo atractivo . Por el contrario, la iteración puede dar la apariencia de puntos que divergen de un solo punto; este sería el caso de un punto fijo inestable . ^[10]

Cuando los puntos de la órbita convergen hacia uno o más límites, el conjunto de puntos de acumulación de la órbita se conoce como conjunto límite o conjunto ω-límite .

Las ideas de atracción y repulsión se generalizan de manera similar; se pueden clasificar las iteraciones en conjuntos estables y conjuntos inestables , según el comportamiento de los pequeños barrios bajo iteración. Véase también infinitas composiciones de funciones analíticas .

Son posibles otras conductas limitantes; por ejemplo, los puntos errantes son puntos que se alejan y nunca regresan ni siquiera cerca de donde comenzaron.

Medida invariante

Si se considera la evolución de una distribución de densidad, en lugar de la dinámica de puntos individuales, entonces el comportamiento límite viene dado por la medida invariante . Puede visualizarse como el comportamiento de una nube de puntos o de polvo bajo iteraciones repetidas. La medida invariante es un estado propio del operador Ruelle-Frobenius-Perron u operador de transferencia , correspondiente a un valor propio de 1. Los valores propios más pequeños corresponden a estados inestables y en decadencia.

En general, debido a que la iteración repetida corresponde a un turno, el operador de transferencia y su adjunto, el operador Koopman puede interpretarse como la acción del operador de turno en un espacio de turno . La teoría de los subdesplazamientos de tipo finito proporciona una visión general de muchas funciones iteradas, especialmente aquellas que conducen al caos.

Iteraciones y flujos fraccionarios e iteraciones negativas

g : R → R es una quinta raíz funcional trivial de f : R ⁺ → R ⁺ , f ( x ) = sin ( x ) .Se muestrael cálculo de f ( π ⁄ 6 ) = 1 ⁄ 2 = g ⁵ ( π ⁄ 6 ).

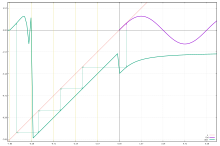
La noción f ^{1/ n} debe usarse con cuidado cuando la ecuación g ⁿ ( x ) = f ( x ) tiene múltiples soluciones, lo que suele ser el caso, como en la ecuación de Babbage de las raíces funcionales del mapa de identidad. Por ejemplo, para n = 2 y f ( x ) = 4 x − 6 , tanto g ( x ) = 6 − 2 x como g ( x ) = 2 x − 2 son soluciones; entonces la expresión f ^1/2 ( x ) no denota una función única, del mismo modo que los números tienen múltiples raíces algebraicas. La cuestión es bastante similar a la expresión " 0/0 " en aritmética. Siempre se puede obtener una raíz trivial de f si el dominio de f se puede extender lo suficiente, cf. imagen. Las raíces elegidas normalmente son las pertenecientes a la órbita en estudio.

Se puede definir la iteración fraccionaria de una función: por ejemplo, la media iteración de una función f es una función g tal que g ( g ( x )) = f ( x ) . ^[11] Esta función g ( x ) se puede escribir usando la notación de índice como f ^1/2 ( x ) . De manera similar, f ^1/3 ( x ) es la función definida de manera que f ^1/3 ( f ^1/3 ( f ^1/3 ( x ))) = f ( x ) , mientras que f ^2/3 ( x ) puede ser definido como igual a f ^1/3 ( f ^1/3 ( x ) ) , y así sucesivamente, todo basado en el principio, mencionado anteriormente, de que f ^m ○ f ⁿ = f ^{m + n} . Esta idea se puede generalizar de modo que el recuento de iteraciones n se convierta en un parámetro continuo , una especie de "tiempo" continuo de una órbita continua . ^{[12] [13]}

En tales casos, uno se refiere al sistema como un flujo (consulte la sección sobre conjugación a continuación).

Si una función es biyectiva (y por lo tanto posee una función inversa), entonces las iteraciones negativas corresponden a funciones inversas y sus composiciones. Por ejemplo, f ⁻¹ ( x ) es la inversa normal de f , mientras que f ⁻² ( x ) es la inversa compuesta consigo misma, es decir, f ⁻² ( x ) = f ⁻¹ ( f ⁻¹ ( x ) . Las iteraciones fraccionarias negativas se definen de manera análoga a las fraccionarias positivas; por ejemplo, f ^−1/2 ( x ) se define de manera que f ^−1/2 ( f ^−1/2 ( x )) = f ⁻¹ ( x ) , o, de manera equivalente, tal que f ^−1/2 ( f ^1/2 ( x )) = f ⁰ ( x ) = x .

Algunas fórmulas para iteración fraccionaria.

Uno de varios métodos para encontrar una fórmula en serie para iteración fraccionaria, utilizando un punto fijo, es el siguiente. ^[14]

1. Primero determine un punto fijo para la función tal que f ( a ) = a .
2. Defina f ⁿ ( a ) = a para todo n perteneciente a los reales. Esta, en cierto modo, es la condición adicional más natural que se puede imponer a las iteraciones fraccionarias.
3. Expanda f ⁿ ( x ) alrededor del punto fijo a como una serie de Taylor ,
   $${\displaystyle f^{n}(x)=f^{n}(a)+(x-a)\left.{\frac {d}{dx}}f^{n}(x)\right|_{x=a}+{\frac {(x-a)^{2}}{2}}\left.{\frac {d^{2}}{dx^{2}}}f^{n}(x)\right|_{x=a}+\cdots }$$
4. Expandirse
   $${\displaystyle f^{n}(x)=f^{n}(a)+(x-a)f'(a)f'(f(a))f'(f^{2}(a))\cdots f'(f^{n-1}(a))+\cdots }$$
5. Sustituir en por f ^k ( a ) = a , para cualquier k ,
   $${\displaystyle f^{n}(x)=a+(x-a)f'(a)^{n}+{\frac {(x-a)^{2}}{2}}(f''(a)f'(a)^{n-1})\left(1+f'(a)+\cdots +f'(a)^{n-1}\right)+\cdots }$$
6. Utilice la progresión geométrica para simplificar términos,
   $${\displaystyle f^{n}(x)=a+(x-a)f'(a)^{n}+{\frac {(x-a)^{2}}{2}}(f''(a)f'(a)^{n-1}){\frac {f'(a)^{n}-1}{f'(a)-1}}+\cdots }$$
   Hay un caso especial cuando f '(a) = 1 ,
   $${\displaystyle f^{n}(x)=x+{\frac {(x-a)^{2}}{2}}(nf''(a))+{\frac {(x-a)^{3}}{6}}\left({\frac {3}{2}}n(n-1)f''(a)^{2}+nf'''(a)\right)+\cdots }$$

Esto puede llevarse a cabo indefinidamente, aunque de manera ineficiente, a medida que estos últimos términos se vuelven cada vez más complicados. En la siguiente sección sobre conjugación se describe un procedimiento más sistemático .

Ejemplo 1

Por ejemplo, establecer f ( x ) = Cx + D da el punto fijo a = D /(1 − C ) , por lo que la fórmula anterior termina en solo

$${\displaystyle f^{n}(x)={\frac {D}{1-C}}+\left(x-{\frac {D}{1-C}}\right)C^{n}=C^{n}x+{\frac {1-C^{n}}{1-C}}D~,}$$

Ejemplo 2

Encuentre el valor de donde esto se hace n veces (y posiblemente los valores interpolados cuando n no es un número entero). Tenemos f ( x ) = √ 2 ^x . Un punto fijo es a = f (2) = 2 . ${\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdots }}}}$

Entonces, conjunto x = 1 y f ⁿ (1) expandido alrededor del valor del punto fijo de 2 es entonces una serie infinita,

$${\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdots }}}=f^{n}(1)=2-(\ln 2)^{n}+{\frac {(\ln 2)^{n+1}((\ln 2)^{n}-1)}{4(\ln 2-1)}}-\cdots }$$

nTetraciónf ⁿ (1) = ⁿ √ 2a = f (4) = 4

Para n = −1 , la serie calcula la función inversa 2+en x/en 2.

Ejemplo 3

Con la función f ( x ) = x ^b , expande alrededor del punto fijo 1 para obtener la serie

$${\displaystyle f^{n}(x)=1+b^{n}(x-1)+{\frac {1}{2}}b^{n}(b^{n}-1)(x-1)^{2}+{\frac {1}{3!}}b^{n}(b^{n}-1)(b^{n}-2)(x-1)^{3}+\cdots ~,}$$

x ^{( b n )}

conjugación

Si f y g son dos funciones iteradas y existe un homeomorfismo h tal que g = h ⁻¹ ○ f ○ h , entonces se dice que f y g son topológicamente conjugados .

Claramente, la conjugación topológica se conserva en la iteración, ya que g ⁿ  =  h ⁻¹  ○  f ⁿ ○ h . Por lo tanto, si se puede resolver un sistema de funciones iteradas, también se tienen soluciones para todos los sistemas topológicamente conjugados. Por ejemplo, el mapa de la tienda está topológicamente conjugado con el mapa logístico . Como caso especial, tomando f ( x ) = x  + 1 , se tiene la iteración de g ( x ) = h ⁻¹ ( h ( x ) + 1 ) como

g ⁿ ( x ) = h ⁻¹ ( h ( x ) +  n ) , para cualquier función h .

Haciendo la sustitución x = h ⁻¹ ( y ) = ϕ ( y ) se obtiene

g ( ϕ ( y )) = ϕ ( y +1) , una forma conocida como ecuación de Abel .

Incluso en ausencia de un homeomorfismo estricto, cerca de un punto fijo, aquí considerado en x = 0, f (0) = 0, a menudo se puede resolver ^[15] la ecuación de Schröder para una función Ψ, que hace que f ( x ) conjugar localmente a una mera dilatación, g ( x ) = f '(0) x , es decir

f ( x ) = Ψ ⁻¹ ( f '(0) Ψ( x )) .

Por lo tanto, su órbita de iteración, o flujo, bajo disposiciones adecuadas (por ejemplo, f '(0) ≠ 1 ), equivale al conjugado de la órbita del monomio,

Ψ ⁻¹ ( f '(0) ⁿ Ψ( x )) ,

donde n en esta expresión sirve como exponente simple: ¡ la iteración funcional se ha reducido a la multiplicación! Aquí, sin embargo, el exponente n ya no necesita ser entero o positivo, y es un "tiempo" continuo de evolución para la órbita completa: ^[16] el monoide de la secuencia de Picard (cf. semigrupo de transformación ) se ha generalizado a un continuo completo grupo . ^[17]

Itera la función seno ( azul ), en el primer medio período. Semiiterado ( naranja ), es decir, la raíz cuadrada funcional del seno; la raíz cuadrada funcional de eso, el cuarto de iteración (negro) encima; y más iteraciones fraccionarias hasta el 1/64. Las funciones debajo del seno ( azul ) son seis iteraciones integrales debajo de él, comenzando con la segunda iteración ( rojo ) y terminando con la iteración número 64. El triángulo envolvente verde representa la iteración nula límite, y la función de diente de sierra sirve como punto de partida que conduce a la función seno. La línea discontinua es la primera iteración negativa, es decir, la inversa del seno (arcsin). (Del sitio web de pedagogía general. ^[18] Para la notación, consulte [2].)

Este método (determinación perturbativa de la función propia principal Ψ, cf. matriz de Carleman ) es equivalente al algoritmo de la sección anterior, aunque, en la práctica, más potente y sistemático.

cadenas de markov

Si la función es lineal y puede describirse mediante una matriz estocástica , es decir, una matriz cuyas filas o columnas suman uno, entonces el sistema iterado se conoce como cadena de Markov .

Ejemplos

Hay muchos mapas caóticos . Las funciones iteradas más conocidas incluyen el conjunto de Mandelbrot y los sistemas de funciones iteradas .

Ernst Schröder , ^[19] en 1870, resolvió casos especiales del mapa logístico , como el caso caótico f ( x ) = 4 x (1 − x ) , de modo que Ψ( x ) = arcsin( √ x ) ² , por lo tanto f ⁿ ( x ) = sin(2 ⁿ arcsin( √ x )) ² .

Un caso no caótico que Schröder también ilustró con su método, f ( x ) = 2 x (1 − x ) , produjo Ψ( x ) = −1/2ln(1 − 2 x ) , y por tanto f ⁿ ( x ) = −1/2((1 - 2 x ) ^{2 norte} - 1) .

Si f es la acción de un elemento de grupo sobre un conjunto, entonces la función iterada corresponde a un grupo libre .

La mayoría de las funciones no tienen expresiones generales explícitas de forma cerrada para la enésima iteración. La siguiente tabla enumera algunos ^[19] que sí lo hacen. Tenga en cuenta que todas estas expresiones son válidas incluso para n no enteros y negativos , así como para n enteros no negativos .

Nota: estos dos casos especiales de ax ² + bx + c son los únicos casos que tienen una solución en forma cerrada. Elegir b = 2 = – a y b = 4 = – a , respectivamente, los reduce aún más a los casos logísticos caóticos y no caóticos discutidos antes de la tabla.

Algunos de estos ejemplos están relacionados entre sí mediante conjugaciones simples.

Medios de estudio

Las funciones iteradas se pueden estudiar con la función zeta de Artin-Mazur y con operadores de transferencia .

en informática

En informática , las funciones iteradas ocurren como un caso especial de funciones recursivas , que a su vez anclan el estudio de temas tan amplios como el cálculo lambda , o otros más restringidos, como la semántica denotacional de los programas de computadora.

Definiciones en términos de funciones iteradas.

Se pueden definir dos funcionales importantes en términos de funciones iteradas. Estos son sumarios :

${\displaystyle \left\{b+1,\sum _{i=a}^{b}g(i)\right\}\equiv \left(\{i,x\}\rightarrow \{i+1,x+g(i)\}\right)^{b-a+1}\{a,0\}}$

y el producto equivalente:

${\displaystyle \left\{b+1,\prod _{i=a}^{b}g(i)\right\}\equiv \left(\{i,x\}\rightarrow \{i+1,xg(i)\}\right)^{b-a+1}\{a,1\}}$

Derivado funcional

La derivada funcional de una función iterada viene dada por la fórmula recursiva:

${\displaystyle {\frac {\delta f^{N}(x)}{\delta f(y)}}=f'(f^{N-1}(x)){\frac {\delta f^{N-1}(x)}{\delta f(y)}}+\delta (f^{N-1}(x)-y)}$

Ecuación de transporte de datos de Lie

Las funciones iteradas surgen en la expansión en serie de funciones combinadas, como g ( f ( x )) .

Dada la velocidad de iteración , o función beta (física) ,

${\displaystyle v(x)=\left.{\frac {\partial f^{n}(x)}{\partial n}}\right|_{n=0}}$

para la n- ^ésima iteración de la función f , tenemos ^[21]

${\displaystyle g(f(x))=\exp \left[v(x){\frac {\partial }{\partial x}}\right]g(x).}$

Por ejemplo, para advección rígida, si f ( x ) = x + t , entonces v ( x ) = t . En consecuencia, g ( x + t ) = exp( t ∂/∂ x ) g ( x ) , acción realizada por un operador de desplazamiento simple .

Por el contrario, se puede especificar f ( x ) dado un v ( x ) arbitrario, a través de la ecuación genérica de Abel analizada anteriormente,

${\displaystyle f(x)=h^{-1}(h(x)+1),}$

dónde

${\displaystyle h(x)=\int {\frac {1}{v(x)}}\,dx.}$

Esto es evidente al observar que

${\displaystyle f^{n}(x)=h^{-1}(h(x)+n)~.}$

Para el índice de iteración continua t , entonces, ahora escrito como un subíndice, esto equivale a la célebre realización exponencial de Lie de un grupo continuo,

${\displaystyle e^{t~{\frac {\partial ~~}{\partial h(x)}}}g(x)=g(h^{-1}(h(x)+t))=g(f_{t}(x)).}$

La velocidad del flujo inicial v es suficiente para determinar todo el flujo, dada esta realización exponencial que proporciona automáticamente la solución general a la ecuación funcional de traslación , ^[22]

${\displaystyle f_{t}(f_{\tau }(x))=f_{t+\tau }(x)~.}$

Ver también

• Rotación irracional
• Sistema de funciones iteradas
• método iterativo
• Número de rotación
• teorema de sarkovskii
• calculo fraccionario
• Relación de recurrencia
• ecuación de schröder
• raíz cuadrada funcional
• función abel
• ecuación de schröder
• La ecuación de Böttcher
• Composiciones infinitas de funciones analíticas.
• Flujo (matemáticas)
• Tetración
• Ecuación funcional

Notas

1. mientras que f ^{( n )} se toma como la enésima derivada
2. ⁿ f ( x ) de Alfred Pringsheim y Jules Molk (1907) para denotar composiciones de funciones no debe confundirse con la notación ⁿ x de Rudolf von Bitter Rucker (1982) , introducida por Hans Maurer (1901) y Reuben. Louis Goodstein (1947) para la tetración , o con la notación presuperíndice ⁿ x de David Patterson Ellerman (1995) para raíces .

Referencias

1. Herschel, John Frederick William (1813) [12 de noviembre de 1812]. "Sobre una aplicación notable del teorema de Cotes". Transacciones filosóficas de la Royal Society de Londres . 103 (Parte 1). Londres: Royal Society of London , impreso por W. Bulmer and Co., Cleveland-Row, St. James's, vendido por G. y W. Nicol, Pall-Mall: 8–26 [10]. doi : 10.1098/rstl.1813.0005 . JSTOR  107384. S2CID  118124706.
2. Herschel, John Federico William (1820). "Parte III. Sección I. Ejemplos del Método Directo de Diferencias". Una colección de ejemplos de aplicaciones del cálculo de diferencias finitas . Cambridge, Reino Unido: Impreso por J. Smith, vendido por J. Deighton & sons. págs. 1 a 13 [5 a 6]. Archivado desde el original el 4 de agosto de 2020 . Consultado el 4 de agosto de 2020 .[1] (NB. Aquí, Herschel se refiere a su obra de 1813 y menciona la obra más antigua de Hans Heinrich Bürmann ).
3. Peano, Giuseppe (1903). Formulario matemático (en francés). vol. IV. pag. 229.
4. Cajori, Florian (1952) [marzo de 1929]. "§472. La potencia de un logaritmo / §473. Logaritmos iterados / §533. Notación de John Herschel para funciones inversas / §535. Persistencia de notaciones rivales para funciones inversas / §537. Potencias de funciones trigonométricas". Una historia de las notaciones matemáticas. vol. 2 (tercera impresión corregida del número de 1929, 2ª ed.). Chicago, Estados Unidos: editorial Open Court . págs.108, 176-179, 336, 346. ISBN 978-1-60206-714-1. Consultado el 18 de enero de 2016 . […] Artículo 473. Logaritmos iterados […] Observamos aquí el simbolismo utilizado por Pringsheim y Molk en su artículo conjunto de la Encyclopédie : " ² log _b  a = log _b (log _b  a ), …, ^{k +1} log _b  a = log _b ( ^k log _b  a )." ^[a] […] §533. La notación de John Herschel para funciones inversas, sin ⁻¹  x , tan ⁻¹  x , etc., fue publicada por él en Philosophical Transactions of London , para el año 1813. Dice (p. 10): "Esta notación cos . ⁻¹  e no debe entenderse en el sentido de 1/cos.  e , sino lo que normalmente se escribe así, arc (cos.= e )." Admite que algunos autores utilizan cos. ^m  A para (cos.  A ) ^m , pero justifica su propia notación señalando que dado que d ²  x , Δ ³  x , Σ ²  x significan dd  x , ΔΔΔ  x , ΣΣ  x , debemos escribir pecado. ²  x por el pecado. pecado.  x , iniciar sesión. ³  x para troncos. registro. registro.  X . Así como escribimos d ^{− n}  V=∫ ⁿ  V, podemos escribir de manera similar sin. ⁻¹  x =arco (sen.= x ), log. ⁻¹  x .=c ^​​x . Algunos años más tarde, Herschel explicó que en 1813 usó f ⁿ ( x ), f ^{− n} ( x ), sin. ⁻¹  x , etc. ", como supuso entonces por primera vez. Sin embargo, en estos pocos meses ha llegado a su conocimiento el trabajo de un analista alemán, Burmann , en el que se explica lo mismo en una fecha mucho anterior. .Él[Burmann], sin embargo, no parece haber advertido la conveniencia de aplicar esta idea a las funciones inversas tan ⁻¹, etc., ni parece en absoluto consciente del cálculo inverso de funciones al que da lugar". Herschel añade: "La simetría de esta notación y, sobre todo, las nuevas y más amplias perspectivas que abre sobre la naturaleza de las operaciones analíticas parecen autorizar su adopción universal." ^[b] […] §535. Persistencia de notaciones rivales para función inversa. — […] El uso de la notación de Herschel sufrió un ligero cambio en los libros de Benjamin Peirce , para eliminar la objeción principal a ellos; Peirce escribió: "cos ^[-1]  x ", "log ^[-1]  x ". ^[c] […] §537. Potencias de funciones trigonométricas. —Se han utilizado tres notaciones principales para denotar, digamos, el cuadrado de sen  x , es decir, (sen  x ) ² , sen  x ² , sen ²  x . La notación predominante en la actualidad es sen ²  x , aunque es menos probable que la primera se malinterprete. En el caso de sen ²  x dos se sugieren interpretaciones; primero, sen  x · sen  x ; segundo, ^[d] sen (sin  x ). Como las funciones del último tipo normalmente no se presentan, el peligro de una mala interpretación es mucho menor que en el caso de log ²  x , donde log  x · log  x y log (log  x ) son frecuentes en el análisis. […] La notación sen ⁿ  x para (sen  x ) ⁿ ha sido ampliamente utilizada y ahora es la que prevalece. […](xviii+367+1 páginas incluyendo 1 página de apéndice) (NB. ISBN y enlace para la reimpresión de la segunda edición de Cosimo, Inc., Nueva York, EE. UU., 2013.)
5. Peirce, Benjamín (1852). Curvas, Funciones y Fuerzas . vol. Yo (nueva ed.). Boston, Estados Unidos. pag. 203.{{cite book}}: CS1 maint: location missing publisher (link)
6. Pringsheim, Alfredo ; Molk, Jules (1907). Encyclopédie des sciences mathématiques pures et appliquées (en francés). vol. I.p. 195. Parte I.
7. Kuczma, Marek (1968). Ecuaciones funcionales en una sola variable . Monografía Matematyczne. Warszawa: PWN - Editores científicos polacos.
8. Kuczma, M., Choczewski B. y Ger, R. (1990). Ecuaciones funcionales iterativas . Prensa de la Universidad de Cambridge. ISBN 0-521-35561-3.{{cite book}}: CS1 maint: multiple names: authors list (link)
9. Carleson, L.; Gamelin, TDW (1993). Dinámica compleja . Universitext: Tratados de Matemáticas. Springer-Verlag. ISBN 0-387-97942-5.
10. Istratescu, Vasile (1981). Teoría del punto fijo, introducción , D. Reidel, Holanda. ISBN 90-277-1224-7 . 
11. "Encontrar f tal que f(f(x))=g(x) dado g". Desbordamiento matemático .
12. Aldrovandi, R.; Freitas, LP (1998). "Iteración continua de mapas dinámicos". J. Matemáticas. Física . 39 (10): 5324. arXiv : física/9712026 . Código bibliográfico : 1998JMP....39.5324A. doi : 10.1063/1.532574. hdl : 11449/65519 . S2CID  119675869.
13. Berkolaiko, G.; Rabinovich, S.; Havlin, S. (1998). "Análisis de la representación de Carleman de recursiones analíticas". J. Matemáticas. Anal. Aplica . 224 : 81–90. doi : 10.1006/jmaa.1998.5986 .
14. "Tetración.org".
15. Kimura, Tosihusa (1971). "Sobre la iteración de funciones analíticas", Funkcialaj Ekvacioj Archivado el 26 de abril de 2012 en Wayback Machine 14 , 197-238.
16. Curtright, TL ; Zachos, CK (2009). "Perfiles de evolución y ecuaciones funcionales". Revista de Física A. 42 (48): 485208. arXiv : 0909.2424 . Código Bib : 2009JPhA...42V5208C. doi :10.1088/1751-8113/42/48/485208. S2CID  115173476.
17. Por ejemplo explícito, el ejemplo 2 anterior equivale simplemente a f ⁿ ( x ) = Ψ ⁻¹ ((ln 2) ⁿ Ψ( x )) , para cualquier n , no necesariamente un número entero, donde Ψ es la solución de la ecuación de Schröder relevante , Ψ( √ 2 ^x ) = ln 2 Ψ( x ) . Esta solución es también el límite infinito m de ( f ^m ( x ) − 2)/(ln 2) ^m .
18. Curtright, superficies TL Evolution y métodos funcionales de Schröder.
19. Schröder, Ernst (1870). "Ueber iterirte Functionen". Matemáticas. Ana . 3 (2): 296–322. doi :10.1007/BF01443992. S2CID  116998358.
20. Brand, Louis, "Una secuencia definida por una ecuación en diferencias", American Mathematical Monthly 62 , septiembre de 1955, 489–492. en línea
21. Berkson, E.; Porta, H. (1978). "Semigrupos de funciones analíticas y operadores de composición". La revista de matemáticas de Michigan . 25 : 101-115. doi : 10.1307/mmj/1029002009 . Curtright, TL; Zachos, CK (2010). "Mapas caóticos, flujos hamiltonianos y métodos holográficos". Revista de Física A: Matemática y Teórica . 43 (44): 445101. arXiv : 1002.0104 . Código Bib : 2010JPhA...43R5101C. doi :10.1088/1751-8113/43/44/445101. S2CID  115176169.
22. Aczel, J. (2006), Conferencias sobre ecuaciones funcionales y sus aplicaciones (Dover Books on Mathematics, 2006), cap. 6, ISBN 978-0486445236 . 

enlaces externos

• Gill, John (enero de 2017). "Introducción a la teoría elemental de composiciones infinitas de funciones complejas". Universidad Estatal de Colorado.