Regla de sucesión

Fórmula en la teoría de la probabilidad

En teoría de probabilidad , la regla de sucesión es una fórmula introducida en el siglo XVIII por Pierre-Simon Laplace al tratar el problema del amanecer . ^[1] La fórmula todavía se utiliza, en particular para estimar probabilidades subyacentes cuando hay pocas observaciones o eventos que no se ha observado que ocurran en absoluto en datos de muestra (finitos).

Enunciado de la regla de sucesión

Si repetimos un experimento que sabemos que puede resultar en éxito o fracaso, n veces independientemente, y obtenemos s éxitos y n − s fracasos, ¿cuál es la probabilidad de que la siguiente repetición tenga éxito?

De manera más abstracta: si X ₁ , ..., X _{n +1} son variables aleatorias condicionalmente independientes que cada una puede asumir el valor 0 o 1, entonces, si no sabemos nada más sobre ellas,

${\displaystyle P(X_{n+1}=1\mid X_{1}+\cdots +X_{n}=s)={s+1 \over n+2}.}$

Interpretación

Dado que sabemos de antemano que estamos ante un experimento en el que es posible tanto el éxito como el fracaso, nuestra estimación es como si hubiéramos observado un éxito y un fracaso con seguridad antes incluso de empezar los experimentos. En cierto sentido, hicimos n  + 2 observaciones (conocidas como pseudocuentas ) con s  + 1 éxitos. Aunque esta puede parecer la suposición más simple y razonable, que también resulta ser cierta, todavía requiere una prueba. De hecho, suponer una pseudocuenta de uno por posibilidad es una forma de generalizar el resultado binario, pero tiene consecuencias inesperadas (véase Generalización a cualquier número de posibilidades, más adelante).

Sin embargo, si no hubiéramos sabido desde el principio que tanto el éxito como el fracaso son posibles, entonces habríamos tenido que asignar

${\displaystyle P'(X_{n+1}=1\mid X_{1}+\cdots +X_{n}=s)={s \over n}.}$

Pero véase Detalles matemáticos, más adelante, para un análisis de su validez. En particular, no es válida cuando , o . ${\displaystyle s=0}$ ${\displaystyle s=n}$

Si el número de observaciones aumenta y se vuelven cada vez más similares, lo cual es intuitivamente claro: cuanto más datos tengamos, menos importancia debemos asignar a nuestra información previa. ${\displaystyle P}$ ${\displaystyle P'}$

Aplicación histórica al problema del amanecer

Laplace utilizó la regla de sucesión para calcular la probabilidad de que el Sol salga mañana, dado que ha salido todos los días durante los últimos 5000 años. Se obtiene un factor muy grande de aproximadamente 5000 × 365,25, lo que da una probabilidad de aproximadamente 1.826.200 a 1 a favor de que el Sol salga mañana.

Sin embargo, como muestran los detalles matemáticos que se presentan a continuación, la suposición básica para utilizar la regla de sucesión sería que no tenemos conocimiento previo sobre la cuestión de si el Sol saldrá o no mañana, excepto que puede hacerlo en ambas situaciones. Este no es el caso de los amaneceres.

Laplace lo sabía bien, y escribió para concluir el ejemplo del amanecer: «Pero este número es mucho mayor para aquel que, viendo en la totalidad de los fenómenos el principio que regula los días y las estaciones, se da cuenta de que nada en el momento presente puede detener su curso». ^[2] Sin embargo, Laplace fue ridiculizado por este cálculo; sus oponentes ^{[¿ quiénes? ]} no prestaron atención a esa frase, o no comprendieron su importancia. ^[2]

En la década de 1940, Rudolf Carnap investigó una teoría basada en la probabilidad del razonamiento inductivo y desarrolló medidas del grado de confirmación, que consideró como alternativas a la regla de sucesión de Laplace. ^{[3] [4]} Véase también Nuevo enigma de la inducción#Carnap .

Intuición

El punto Z es el punto cero, P es el punto tal que la fracción del círculo de Z a P (en azul) es igual a p . El valor de p es precisamente el número de arcos azules dividido por el número total de arcos. Si dejamos que el primer punto en el sentido de las agujas del reloj de un arco lo defina, entonces cada punto en el círculo define un arco con Z definiendo un arco azul y P definiendo un arco no azul. La estimación para p es entonces uno ( Z ) más puntos azules dividido por dos ( Z y P ) más que el número total de ensayos, que es la regla de sucesión.

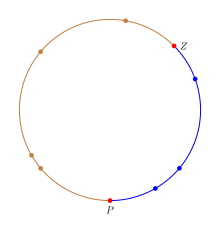
La regla de sucesión se puede interpretar de manera intuitiva considerando puntos distribuidos aleatoriamente en un círculo en lugar de contar el número de "éxitos"/"fracasos" en un experimento. ^[5] Para imitar el comportamiento de la proporción p en el círculo, pintaremos el círculo con dos colores y la fracción del círculo coloreada con el color de "éxito" será igual a p . Para expresar la incertidumbre sobre el valor de p , necesitamos seleccionar una fracción del círculo.

Se elige una fracción seleccionando dos puntos uniformemente aleatorios en el círculo. El primer punto Z corresponde al cero en el intervalo [0, 1] y el segundo punto P corresponde a p dentro de [0, 1]. En términos del círculo, la fracción del círculo desde Z hasta P moviéndose en el sentido de las agujas del reloj será igual a p . Los n ensayos se pueden interpretar como n puntos distribuidos uniformemente en el círculo; cualquier punto en la fracción de "éxito" es un éxito y un fracaso en caso contrario. Esto proporciona una correspondencia exacta de los experimentos de éxito/fracaso con probabilidad de éxito p a puntos uniformemente aleatorios en el círculo. En la figura, la fracción de éxito está coloreada en azul para diferenciarla del resto del círculo y los puntos P y Z están resaltados en rojo.

Dado este círculo, la estimación de p es la fracción coloreada de azul. Dividamos el círculo en n+2 arcos correspondientes a los n+2 puntos de modo que la porción desde un punto del círculo hasta el siguiente punto (moviéndose en el sentido de las agujas del reloj) sea un arco asociado con el primer punto. Por lo tanto, Z define el primer arco azul mientras que P define el primer arco no azul/fallido. Dado que el siguiente punto es un punto uniformemente aleatorio, si cae en cualquiera de los arcos azules, entonces el ensayo tiene éxito, mientras que si cae en cualquiera de los otros arcos, entonces falla. Por lo tanto, la probabilidad de éxito p es donde b es el número de arcos azules y t es el número total de arcos. Nótese que hay un arco azul más (el de Z ) que el punto de éxito y dos arcos más (los de P y Z ) que n puntos. Sustituyendo los valores con el número de éxitos se obtiene la regla de sucesión. ${\displaystyle {\frac {b}{t}}}$

Nota: La probabilidad real debe utilizar la longitud de los arcos azules dividida por la longitud de todos los arcos. Sin embargo, cuando k puntos se distribuyen de manera aleatoria y uniforme en un círculo, la distancia de un punto al siguiente es 1/k. Por lo tanto, en promedio, cada arco tiene la misma longitud y la relación de longitudes se convierte en la relación de conteos.

Detalles matemáticos

A la proporción p se le asigna una distribución uniforme para describir la incertidumbre sobre su valor verdadero. (Esta proporción no es aleatoria, sino incierta. Asignamos una distribución de probabilidad a p para expresar nuestra incertidumbre, no para atribuirle aleatoriedad  . Pero esto equivale, matemáticamente, a lo mismo que tratar a p como si fuera aleatorio).

Sea X _i 1 si observamos un "éxito" en el i ésimo ensayo , de lo contrario 0, con probabilidad p de éxito en cada ensayo. Por lo tanto, cada X es 0 o 1; cada X tiene una distribución de Bernoulli . Supongamos que estas X son condicionalmente independientes dado p .

Podemos utilizar el teorema de Bayes para encontrar la distribución de probabilidad condicional de p dados los datos Xi , _i = 1, ..., n. Para la medida de probabilidad " previa " (es decir, marginal ) de p, asignamos una distribución uniforme sobre el intervalo abierto (0,1).

${\displaystyle f(p)={\begin{cases}0&{\text{for }}p\leq 0\\1&{\text{for }}0<p<1\\0&{\text{for }}p\geq 1\end{cases}}}$

Para la probabilidad de un p dado bajo nuestras observaciones, utilizamos la función de probabilidad

${\displaystyle L(p)=P(X_{1}=x_{1},\ldots ,X_{n}=x_{n}\mid p)=\prod _{i=1}^{n}p^{x_{i}}(1-p)^{1-x_{i}}=p^{s}(1-p)^{n-s}}$

donde s  =  x ₁  + ... +  x _n es el número de "éxitos" y n es el número de ensayos (estamos usando X mayúscula para denotar una variable aleatoria y x minúscula para los datos realmente observados). Poniendo todo junto, podemos calcular la probabilidad posterior:

${\displaystyle f(p\mid X_{1}=x_{1},\ldots ,X_{n}=x_{n})={L(p)f(p) \over \int _{0}^{1}L(r)f(r)\,dr}={p^{s}(1-p)^{n-s} \over \int _{0}^{1}r^{s}(1-r)^{n-s}\,dr}}$

Para obtener la constante normalizadora , encontramos

${\displaystyle \int _{0}^{1}r^{s}(1-r)^{n-s}\,dr={s!(n-s)! \over (n+1)!}}$

(ver función beta para más información sobre integrales de esta forma).

Por lo tanto, la función de densidad de probabilidad posterior es

${\displaystyle f(p\mid X_{1}=x_{1},\ldots ,X_{n}=x_{n})={(n+1)! \over s!(n-s)!}p^{s}(1-p)^{n-s}.}$

Esta es una distribución beta con valor esperado

${\displaystyle \operatorname {E} (p\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)=\int _{0}^{1}pf(p\mid X_{1}=x_{1},\ldots ,X_{n}=x_{n})\,dp={s+1 \over n+2}.}$

Como p nos indica la probabilidad de éxito en cualquier experimento, y cada experimento es condicionalmente independiente , la probabilidad condicional de éxito en el siguiente experimento es simplemente p . Como p se trata como si fuera una variable aleatoria , la ley de probabilidad total nos dice que la probabilidad esperada de éxito en el siguiente experimento es simplemente el valor esperado de p . Como p es condicional a los datos observados X _i para i = 1, ..., n , tenemos

${\displaystyle P(X_{n+1}=1\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)=\operatorname {E} (p\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)={s+1 \over n+2}.}$

El mismo cálculo se puede realizar con la anterior (impropia) que expresa ignorancia total de p , incluida la ignorancia con respecto a la cuestión de si el experimento puede tener éxito o puede fallar. Esta anterior impropia es 1/( p (1 −  p )) para 0 ≤  p  ≤ 1 y 0 en caso contrario. ^[6] Si se repite el cálculo anterior con esta anterior, obtenemos

${\displaystyle P'(X_{n+1}=1\mid X_{i}=x_{i}{\text{ for }}i=1,\dots ,n)={s \over n}.}$

Por lo tanto, con la distribución previa que especifica la ignorancia total, la probabilidad de éxito está gobernada por la frecuencia observada de éxito. Sin embargo, la distribución posterior que llevó a este resultado es la distribución Beta( s , n  −  s ), que no es adecuada cuando s  =  n o s  = 0 (es decir, la constante de normalización es infinita cuando s  = 0 o s  =  n ). Esto significa que no podemos usar esta forma de la distribución posterior para calcular la probabilidad de que la siguiente observación tenga éxito cuando s  = 0 o s  =  n . Esto pone la información contenida en la regla de sucesión en mayor luz: puede considerarse como la expresión de la suposición previa de que si el muestreo se continuara indefinidamente, eventualmente observaríamos al menos un éxito y al menos un fracaso en la muestra. La distribución previa que expresa la ignorancia total no presupone este conocimiento.

Para evaluar el caso de "ignorancia total" cuando s  = 0 o s  =  n se puede manejar, primero volvemos a la distribución hipergeométrica , denotada por . Este es el enfoque adoptado en Jaynes (2003). La binomial se puede derivar como una forma límite, donde de tal manera que su proporción permanece fija. Se puede pensar en como el número de éxitos en la población total, de tamaño . ${\displaystyle \mathrm {Hyp} (s|N,n,S)}$ ${\displaystyle \mathrm {Bin} (r|n,p)}$ ${\displaystyle N,S\rightarrow \infty }$ ${\displaystyle p={S \over N}}$ ${\displaystyle S}$ ${\displaystyle N}$

El equivalente anterior a es , con un dominio de . Trabajar con condiciones a significa que estimar es equivalente a estimar , y luego dividir esta estimación por . La posterior para se puede dar como: ${\displaystyle {1 \over p(1-p)}}$ ${\displaystyle {1 \over S(N-S)}}$ ${\displaystyle 1\leq S\leq N-1}$ ${\displaystyle N}$ ${\displaystyle p}$ ${\displaystyle S}$ ${\displaystyle N}$ ${\displaystyle S}$

${\displaystyle P(S|N,n,s)\propto {1 \over S(N-S)}{S \choose s}{N-S \choose n-s}\propto {S!(N-S)! \over S(N-S)(S-s)!(N-S-[n-s])!}}$

Y se puede ver que, si s  =  n o s  = 0, entonces uno de los factoriales en el numerador se cancela exactamente con uno en el denominador. Tomando el caso s  = 0, tenemos:

${\displaystyle P(S|N,n,s=0)\propto {(N-S-1)! \over S(N-S-n)!}={\prod _{j=1}^{n-1}(N-S-j) \over S}}$

Si sumamos la constante normalizadora, que siempre es finita (porque no hay singularidades en el rango de la posterior y hay un número finito de términos), obtenemos:

${\displaystyle P(S|N,n,s=0)={\prod _{j=1}^{n-1}(N-S-j) \over S\sum _{R=1}^{N-n}{\prod _{j=1}^{n-1}(N-R-j) \over R}}}$

Por lo tanto, la expectativa posterior es: ${\displaystyle p={S \over N}}$

${\displaystyle E\left({S \over N}|n,s=0,N\right)={1 \over N}\sum _{S=1}^{N-n}SP(S|N,n=1,s=0)={1 \over N}{\sum _{S=1}^{N-n}\prod _{j=1}^{n-1}(N-S-j) \over \sum _{R=1}^{N-n}{\prod _{j=1}^{n-1}(N-R-j) \over R}}}$

Una expresión analítica aproximada para un número N grande se obtiene haciendo primero la aproximación al término del producto:

${\displaystyle \prod _{j=1}^{n-1}(N-R-j)\approx (N-R)^{n-1}}$

y luego reemplazando la suma en el numerador con una integral

${\displaystyle \sum _{S=1}^{N-n}\prod _{j=1}^{n-1}(N-S-j)\approx \int _{1}^{N-n}(N-S)^{n-1}\,dS={(N-1)^{n}-n^{n} \over n}\approx {N^{n} \over n}}$

Se sigue el mismo procedimiento para el denominador, pero el proceso es un poco más complicado, ya que la integral es más difícil de evaluar.

${\displaystyle {\begin{aligned}\sum _{R=1}^{N-n}{\prod _{j=1}^{n-1}(N-R-j) \over R}&\approx \int _{1}^{N-n}{(N-R)^{n-1} \over R}\,dR\\&=N\int _{1}^{N-n}{(N-R)^{n-2} \over R}\,dR-\int _{1}^{N-n}(N-R)^{n-2}\,dR\\&=N^{n-1}\left[\int _{1}^{N-n}{dR \over R}-{1 \over n-1}+O\left({1 \over N}\right)\right]\approx N^{n-1}\ln(N)\end{aligned}}}$

donde ln es el logaritmo natural. Introduciendo estas aproximaciones en la expectativa se obtiene

${\displaystyle E\left({S \over N}|n,s=0,N\right)\approx {1 \over N}{{N^{n} \over n} \over N^{n-1}\ln(N)}={1 \over n[\ln(N)]}={\log _{10}(e) \over n[\log _{10}(N)]}={0.434294 \over n[\log _{10}(N)]}}$

donde se ha utilizado el logaritmo de base 10 en la respuesta final para facilitar el cálculo. Por ejemplo, si la población tiene un tamaño de 10 ^k , la probabilidad de éxito en la siguiente muestra viene dada por:

${\displaystyle E\left({S \over N}\mid n,s=0,N=10^{k}\right)\approx {0.434294 \over nk}}$

Por ejemplo, si la población es del orden de decenas de miles de millones, de modo que k  = 10, y observamos n  = 10 resultados sin éxito, entonces la proporción esperada en la población es aproximadamente 0,43%. Si la población es menor, de modo que n  = 10, k  = 5 (decenas de miles), la proporción esperada aumenta a aproximadamente 0,86%, y así sucesivamente. De manera similar, si el número de observaciones es menor, de modo que n  = 5, k  = 10, la proporción aumenta a aproximadamente 0,86% nuevamente.

Esta probabilidad no tiene límite inferior positivo y puede hacerse arbitrariamente pequeña para elecciones cada vez mayores de N o k . Esto significa que la probabilidad depende del tamaño de la población de la que se está muestreando. Al pasar al límite de N infinito (para las propiedades analíticas más simples) estamos "desechando" un fragmento de información muy importante. Nótese que esta relación de ignorancia solo se cumple mientras no se observe ningún éxito. Se revisa correspondientemente de nuevo a la regla de frecuencia observada tan pronto como se observa un éxito. Los resultados correspondientes se encuentran para el caso s=n intercambiando las etiquetas y luego restando la probabilidad de 1. ${\displaystyle p={s \over n}}$

Generalización a cualquier número de posibilidades.

Esta sección ofrece una derivación heurística similar a la de Teoría de la probabilidad: la lógica de la ciencia . ^[7]

La regla de sucesión tiene muchas interpretaciones intuitivas diferentes y, según la intuición que se utilice, la generalización puede ser diferente. Por lo tanto, la forma de proceder a partir de aquí es con mucho cuidado y derivando nuevamente los resultados a partir de los primeros principios, en lugar de introducir una generalización intuitivamente sensata. La derivación completa se puede encontrar en el libro de Jaynes, pero admite una derivación alternativa más fácil de entender, una vez que se conoce la solución. Otro punto que se debe enfatizar es que el estado previo de conocimiento descrito por la regla de sucesión se da como una enumeración de las posibilidades, con la información adicional de que es posible observar cada categoría. Esto se puede expresar de manera equivalente como observar cada categoría una vez antes de recopilar los datos. Para indicar que este es el conocimiento utilizado, se coloca un Im como parte de las condiciones en las asignaciones de probabilidad _.

La regla de sucesión se obtiene al establecer una probabilidad binomial y una distribución previa uniforme. Por lo tanto, una generalización sencilla es simplemente la extensión multivariante de estas dos distribuciones: 1) Establecer una distribución previa uniforme sobre las m categorías iniciales y 2) usar la distribución multinomial como la función de probabilidad (que es la generalización multivariante de la distribución binomial). Se puede demostrar que la distribución uniforme es un caso especial de la distribución de Dirichlet con todos sus parámetros iguales a 1 (así como la distribución uniforme es Beta(1,1) en el caso binario). La distribución de Dirichlet es la distribución previa conjugada para la distribución multinomial, lo que significa que la distribución posterior también es una distribución de Dirichlet con diferentes parámetros. Sea p _i la probabilidad de que se observe la categoría i y sea n _i el número de veces que se observó realmente la categoría i ( i  = 1, ...,  m ). Entonces, la distribución posterior conjunta de las probabilidades p ₁ , ...,  p _m viene dada por:

${\displaystyle f(p_{1},\ldots ,p_{m}\mid n_{1},\ldots ,n_{m},I)={\begin{cases}{\displaystyle {\frac {\Gamma \left(\sum _{i=1}^{m}(n_{i}+1)\right)}{\prod _{i=1}^{m}\Gamma (n_{i}+1)}}p_{1}^{n_{1}}\cdots p_{m}^{n_{m}}},\quad &\sum _{i=1}^{m}p_{i}=1\\\\0&{\text{otherwise.}}\end{cases}}}$

Para obtener la regla generalizada de sucesión, tenga en cuenta que la probabilidad de observar la categoría i en la siguiente observación, condicional a p _i , es simplemente p _i , simplemente requerimos su esperanza. Sea A _i el evento de que la siguiente observación esté en la categoría i ( i  = 1, ...,  m ), y sea n  =  n ₁  + ... +  n _m el número total de observaciones realizadas. El resultado, utilizando las propiedades de la distribución de Dirichlet, es:

${\displaystyle P(A_{i}|n_{1},\ldots ,n_{m},I_{m})={n_{i}+1 \over n+m}.}$

Esta solución se reduce a la probabilidad que se asignaría utilizando el principio de indiferencia antes de que se hicieran observaciones (es decir, n  = 0), de acuerdo con la regla de sucesión original. También contiene la regla de sucesión como un caso especial, cuando m  = 2, como corresponde a una generalización.

Como las proposiciones o eventos A _i son mutuamente excluyentes, es posible agrupar las m categorías en 2. Simplemente sume las probabilidades A _i que corresponden al "éxito" para obtener la probabilidad de éxito. Supongamos que esto agrega c categorías como "éxito" y mc categorías como "fracaso". Sea s la suma de los n _i valores relevantes que se han denominado "éxito". La probabilidad de "éxito" en el siguiente ensayo es entonces:

${\displaystyle P({\text{success}}|n_{1},\ldots ,n_{m},I_{m})={s+c \over n+m},}$

que es diferente de la regla original de sucesión. Pero tenga en cuenta que la regla original de sucesión se basa en I ₂ , mientras que la generalización se basa en I _m . Esto significa que la información contenida en I _m es diferente de la contenida en I ₂ . Esto indica que el mero conocimiento de más de dos resultados que sabemos que son posibles es información relevante cuando se reducen estas categorías a solo dos. Esto ilustra la sutileza en la descripción de la información previa y por qué es importante especificar qué información previa se está utilizando.

Análisis adicional

Un buen modelo es esencial (es decir, un buen equilibrio entre precisión y practicidad). Parafraseando a Laplace sobre el problema de la salida del sol : Aunque tenemos una enorme cantidad de muestras de la salida del sol, hay modelos mucho mejores del sol que suponer que tiene una cierta probabilidad de salir cada día, es decir, simplemente tener una vida media.

Dado un buen modelo, es mejor realizar tantas observaciones como sea posible, dependiendo de la confiabilidad esperada del conocimiento previo, el costo de las observaciones, el tiempo y los recursos disponibles y la precisión requerida.

Uno de los aspectos más difíciles de la regla de sucesión no son las fórmulas matemáticas, sino responder a la pregunta: ¿cuándo se aplica la regla de sucesión? En la sección de generalización, se señaló de manera muy explícita al agregar la información previa _Im a los cálculos. Por lo tanto, cuando todo lo que se sabe sobre un fenómeno es que hay m resultados posibles conocidos antes de observar cualquier dato, solo entonces se aplica la regla de sucesión. Si la regla de sucesión se aplica en problemas en los que no describe con precisión el estado previo de conocimiento, entonces puede dar resultados contraintuitivos. Esto no se debe a que la regla de sucesión sea defectuosa, sino a que en realidad está respondiendo a una pregunta diferente, basada en información previa diferente.

En principio (véase la regla de Cromwell ), ninguna posibilidad debería tener su probabilidad (o su pseudoconteo) fijada en cero, ya que nada en el mundo físico debería asumirse estrictamente imposible (aunque pueda serlo), incluso si es contrario a todas las observaciones y teorías actuales. De hecho, la regla de Bayes no tiene en cuenta en absoluto una observación que previamente se creía que tenía probabilidad cero; sigue declarándose imposible. Sin embargo, considerar solo un conjunto fijo de posibilidades es una ruta aceptable, solo hay que recordar que los resultados están condicionados a (o restringidos a) el conjunto que se está considerando, y no a un conjunto "universal". De hecho, Larry Bretthorst muestra que incluir la posibilidad de "algo más" en el espacio de hipótesis no hace ninguna diferencia en las probabilidades relativas de la otra hipótesis; simplemente las renormaliza para que sumen un valor menor que 1. ^[8] Hasta que se especifique "algo más", la función de probabilidad condicional a este "algo más" es indeterminada, porque ¿cómo se puede determinar ? Por lo tanto, no puede producirse ninguna actualización de la probabilidad previa de "algo más" hasta que se defina con mayor precisión. ${\displaystyle Pr({\text{data}}|{\text{something else}},I)}$

Sin embargo, a veces es discutible si el conocimiento previo debería afectar las probabilidades relativas, o también el peso total del conocimiento previo comparado con las observaciones reales. Esto no tiene una respuesta clara, ya que depende del conocimiento previo que se esté considerando. De hecho, un estado previo alternativo de conocimiento podría ser de la forma "He especificado m categorías potenciales, pero estoy seguro de que solo una de ellas es posible antes de observar los datos. Sin embargo, no sé qué categoría en particular es esta". Una forma matemática de describir este estado previo es la distribución de Dirichlet con todos los parámetros iguales a m ⁻¹ , que luego da un pseudocuenta de 1 al denominador en lugar de m , y agrega un pseudocuenta de m ⁻¹ a cada categoría. Esto da una probabilidad ligeramente diferente en el caso binario de . ${\displaystyle {\frac {s+0.5}{n+1}}}$

Sólo vale la pena invertir un esfuerzo significativo en estimar las probabilidades previas cuando es probable que tengan un efecto significativo. Pueden ser importantes cuando hay pocas observaciones, especialmente cuando son tan pocas que ha habido pocas, si es que ha habido alguna, observación de algunas posibilidades, como un animal raro en una región determinada. También son importantes cuando hay muchas observaciones, cuando se cree que la expectativa debería estar fuertemente ponderada hacia las estimaciones previas, a pesar de muchas observaciones en contra, como en el caso de una ruleta en un casino muy respetado. En este último caso, al menos algunos de los pseudoconteos pueden tener que ser muy grandes. No siempre son pequeños y, por lo tanto, pronto se ven superados por las observaciones reales, como se supone a menudo. Sin embargo, aunque se trata de un último recurso, para los fines cotidianos, el conocimiento previo suele ser vital. Por lo tanto, la mayoría de las decisiones deben ser subjetivas hasta cierto punto (dependiendo del analista y del análisis utilizado).

Véase también

• Suavizado aditivo
• Estimador de Krichevsky-Trofimov
• Principio de indiferencia

Referencias

1. Laplace, Pierre-Simon (1814). Ensayo filosófico sobre las probabilidades. París: Courcier.
2. Parte II Sección 18.6 de Jaynes, ET y Bretthorst, GL (2003). Teoría de la probabilidad: la lógica de la ciencia. Cambridge University Press. ISBN  978-0-521-59271-0
3. Rudolf Carnap (1945). "Sobre la lógica inductiva" (PDF) . Filosofía de la ciencia . 12 (2): 72–97. doi :10.1086/286851. S2CID  14481246.; aquí: p.86, 97
4. Rudolf Carnap (1947). "Sobre la aplicación de la lógica inductiva" (PDF) . Filosofía e investigación fenomenológica . 8 (1): 133–148. doi :10.2307/2102920. JSTOR  2102920.; aquí: p.145
5. Neyman, Eric. "Una prueba elegante de la regla de sucesión de Laplace". Valores inesperados . Eric Neyman . Consultado el 13 de abril de 2023 .
6. http://www.stats.org.uk/priors/noninformative/Smith.pdf ^{[ URL básica PDF ]}
7. Jaynes, ET (2003), Teoría de la probabilidad: la lógica de la ciencia , Cambridge, Reino Unido, Cambridge University Press.
8. Bretthost, G. Larry (1988). Análisis espectral bayesiano y estimación de parámetros (PDF) (tesis doctoral). pág. 55.