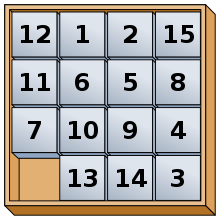
El rompecabezas del 15 (también llamado Rompecabezas de Gemas , Rompecabezas del Jefe , Juego de los Quince , Cuadrado Místico y más) es un rompecabezas deslizante . Tiene 15 fichas cuadradas numeradas del 1 al 15 en un marco que tiene 4 posiciones de fichas de alto y 4 posiciones de fichas de ancho, con una posición desocupada. Las fichas en la misma fila o columna de la posición abierta se pueden mover deslizándolas horizontal o verticalmente, respectivamente. El objetivo del rompecabezas es colocar las fichas en orden numérico (de izquierda a derecha, de arriba a abajo).
El rompecabezas 15, que recibe su nombre por la cantidad de fichas que tiene en el marco, también puede denominarse "rompecabezas 16" , en alusión a su capacidad total de fichas. Se utilizan nombres similares para variantes de diferentes tamaños del rompecabezas 15, como el rompecabezas 8, que tiene 8 fichas en un marco de 3x3.
El rompecabezas n es un problema clásico para modelar algoritmos que involucran heurísticas . Las heurísticas comúnmente utilizadas para este problema incluyen contar la cantidad de fichas mal ubicadas y encontrar la suma de las distancias de taxi entre cada bloque y su posición en la configuración objetivo. [1] Nótese que ambos son admisibles . Es decir, nunca sobreestiman la cantidad de movimientos restantes, lo que asegura la optimalidad para ciertos algoritmos de búsqueda como A* . [1]

Johnson y Story (1879) utilizaron un argumento de paridad para demostrar que la mitad de las posiciones iniciales del rompecabezas n son imposibles de resolver, sin importar cuántos movimientos se realicen. Esto se hace considerando una función binaria de la configuración de las fichas que es invariante ante cualquier movimiento válido y luego usándola para dividir el espacio de todos los estados etiquetados posibles en dos clases de equivalencia mutuamente inaccesibles del mismo tamaño. Esto significa que la mitad de todas las posiciones son irresolubles, aunque no dice nada sobre la mitad restante.
La invariante es la paridad de la permutación de los 16 cuadrados más la paridad de la distancia en taxi (número de filas más número de columnas) del cuadrado vacío desde la esquina inferior derecha. Se trata de una invariante porque cada movimiento cambia tanto la paridad de la permutación como la paridad de la distancia en taxi. En particular, si el cuadrado vacío está en la esquina inferior derecha, el rompecabezas solo se puede resolver si la permutación de las piezas restantes es par.
Johnson y Story (1879) también demostraron que en tableros de tamaño m × n , donde m y n son ambos mayores o iguales a 2, todas las permutaciones pares son solucionables. Esto se puede demostrar por inducción en m y n , comenzando con m = n = 2. Esto significa que hay exactamente dos clases de equivalencia de arreglos mutuamente accesibles, y que la paridad descrita es el único invariante no trivial, aunque existen descripciones equivalentes.
Archer (1999) dio otra prueba, basada en la definición de clases de equivalencia a través de un camino hamiltoniano .
Wilson (1974) estudió la generalización del rompecabezas 15 a grafos finitos arbitrarios , siendo el problema original el caso de un grafo de cuadrícula 4×4 . El problema tiene algunos casos degenerados donde la respuesta es trivial o una simple combinación de las respuestas al mismo problema en algunos subgrafos. Es decir, para caminos y polígonos , el rompecabezas no tiene libertad; si el grafo está desconectado , solo es relevante el componente conectado del vértice con el "espacio vacío"; y si hay un vértice de articulación , el problema se reduce al mismo rompecabezas en cada uno de los componentes biconectados de ese vértice. Excluyendo estos casos, Wilson mostró que, salvo un grafo excepcional en 7 vértices, es posible obtener todas las permutaciones a menos que el grafo sea bipartito , en cuyo caso se pueden obtener exactamente las permutaciones pares. El grafo excepcional es un hexágono regular con una diagonal y un vértice en el centro añadidos; solo1/6Se puede obtener una de sus permutaciones, lo que da un ejemplo de la incrustación exótica de S 5 en S 6 .
Para las versiones más grandes del rompecabezas n , encontrar una solución es fácil. Pero, el problema de encontrar la solución más corta es NP-difícil . También es NP-difícil aproximar la menor cantidad de deslizamientos dentro de una constante aditiva, pero hay una aproximación de factor constante de tiempo polinomial. [2] [3] Para el rompecabezas 15, las longitudes de las soluciones óptimas varían de 0 a 80 movimientos de una sola ficha (hay 17 configuraciones que requieren 80 movimientos) [4] [5] o 43 movimientos de múltiples fichas; [6] el rompecabezas 8 siempre se puede resolver en no más de 31 movimientos de una sola ficha o 24 movimientos de múltiples fichas (secuencia entera A087725). La métrica de múltiples fichas cuenta los movimientos posteriores de la ficha vacía en la misma dirección como uno. [6]
El número de posiciones posibles del rompecabezas 24 es 25!/2 ≈7,76 × 10 24 , que es demasiado para calcular el número de Dios de manera factible utilizando métodos de fuerza bruta. En 2011, se establecieron límites inferiores de 152 movimientos de una sola pieza o 41 movimientos de varias piezas, así como límites superiores de 208 movimientos de una sola pieza o 109 movimientos de varias piezas. [7] [8] [9] [10] En 2016, el límite superior se mejoró a 205 movimientos de una sola pieza. [11]
Las transformaciones del rompecabezas 15 forman un grupoide (no un grupo, ya que no todos los movimientos pueden ser compuestos); [12] [13] [14] este grupoide actúa sobre las configuraciones.
Debido a que las combinaciones del rompecabezas 15 se pueden generar mediante ciclos de 3 , se puede demostrar que el rompecabezas 15 se puede representar mediante el grupo alterno . [15] De hecho, cualquier rompecabezas deslizante con fichas cuadradas de igual tamaño se puede representar mediante .


El rompecabezas fue "inventado" por Noyes Palmer Chapman, [16] un jefe de correos en Canastota, Nueva York , que se dice que mostró a sus amigos, ya en 1874, un rompecabezas precursor que consistía en 16 bloques numerados que debían colocarse juntos en filas de cuatro, cada uno sumando 34 (ver cuadrado mágico ). Copias del rompecabezas de 15 mejorado llegaron a Syracuse, Nueva York , a través del hijo de Chapman, Frank, y desde allí, a través de diversas conexiones, a Watch Hill, Rhode Island , y finalmente a Hartford , Connecticut , donde los estudiantes de la Escuela Americana para Sordos comenzaron a fabricar el rompecabezas. En diciembre de 1879, estos se vendían tanto localmente como en Boston , Massachusetts . Cuando le mostraron uno de estos, Matthias Rice, que tenía un negocio de carpintería en Boston, comenzó a fabricar el rompecabezas en algún momento de diciembre de 1879 y convenció a un comerciante de artículos de lujo "Yankee Notions" para que los vendiera bajo el nombre de "Gem Puzzle". A finales de enero de 1880, Charles Pevey, un dentista de Worcester , Massachusetts, ganó cierta atención al ofrecer una recompensa en efectivo por una solución al rompecabezas 15. [16]
El juego se convirtió en una moda en los EE. UU. en 1880. [17]
Chapman solicitó una patente para su "Block Solitaire Puzzle" el 21 de febrero de 1880. Sin embargo, esta patente fue rechazada, probablemente porque no era lo suficientemente diferente de la patente "Puzzle-Blocks" del 20 de agosto de 1878 (US 207124) otorgada a Ernest U. Kinsey. [16]

Desde 1891 hasta su muerte en 1911, Sam Loyd afirmó haber inventado el rompecabezas. Sin embargo, Loyd no tenía ninguna relación con la invención o la popularidad inicial del rompecabezas. El primer artículo de Loyd sobre el rompecabezas se publicó en 1886, y no fue hasta 1891 cuando afirmó por primera vez ser el inventor. [16] [18]
Un interés posterior fue alimentado por la oferta de Loyd de un premio de $1,000 (equivalente a $33,911 en 2023) a cualquiera que pudiera proporcionar una solución para lograr una combinación particular especificada por Loyd, es decir, invertir el 14 y el 15, lo que Loyd llamó el rompecabezas 14-15 . [1] Esto es imposible, como lo habían demostrado más de una década antes Johnson y Story (1879), porque requiere una transformación de una permutación par a una impar.
El Cubo Minus , fabricado en la URSS , es un rompecabezas 3D con operaciones similares al Rompecabezas 15.
Las versiones del rompecabezas de 15 piezas incluyen una cantidad diferente de fichas, como el rompecabezas de 8 piezas o el de 24 piezas.
El campeón mundial de ajedrez Bobby Fischer era un experto en resolver el problema del 15. [19] Le habían cronometrado para poder resolverlo en 25 segundos; Fischer lo demostró el 8 de noviembre de 1972 en The Tonight Show Starring Johnny Carson . [20] [21]