Retrato de fase

Gráfico de las trayectorias de un sistema dinámico en el espacio de fase.

Retrato de energía potencial y fases de un péndulo simple . Tenga en cuenta que el eje x, al ser angular, se enrolla sobre sí mismo cada 2π radianes.

Retrato de fase de un oscilador amortiguado, con una fuerza de amortiguación creciente. La ecuación del movimiento es ${\displaystyle {\ddot {x}}+2\gamma {\dot {x}}+\omega ^{2}x=0.}$

En matemáticas , un retrato de fase es una representación geométrica de las órbitas de un sistema dinámico en el plano de fase . Cada conjunto de condiciones iniciales está representado por un punto o curva diferente .

Los retratos de fase son una herramienta invaluable en el estudio de sistemas dinámicos. Consisten en un gráfico de trayectorias típicas en el espacio de fases . Esto revela información como si hay un atractor , un repelente o un ciclo límite para el valor del parámetro elegido. El concepto de equivalencia topológica es importante para clasificar el comportamiento de sistemas al especificar cuándo dos retratos de fases diferentes representan el mismo comportamiento dinámico cualitativo. Un atractor es un punto estable que también se llama "sumidero". El repelente se considera un punto inestable, que también se conoce como "fuente".

Un gráfico de retrato de fase de un sistema dinámico representa las trayectorias del sistema (con flechas) y los estados estables estables (con puntos) y los estados estables inestables (con círculos) en un espacio de fase. Los ejes son de variables de estado .

Ejemplos

Ilustración de cómo se construiría un retrato de fase para el movimiento de un péndulo simple.

Retrato de fase de la ecuación de van der Pol ,. ${\displaystyle {\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0}$

• Péndulo simple , ver imagen (derecha).
• Oscilador armónico simple donde el retrato de fase está formado por elipses centradas en el origen, que es un punto fijo.
• Movimiento armónico amortiguado , ver animación (derecha).
• Oscilador de Van der Pol ver imagen (abajo a la derecha).

Visualizando el comportamiento de ecuaciones diferenciales ordinarias.

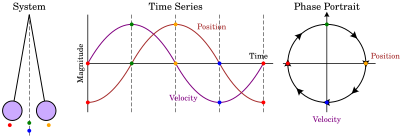
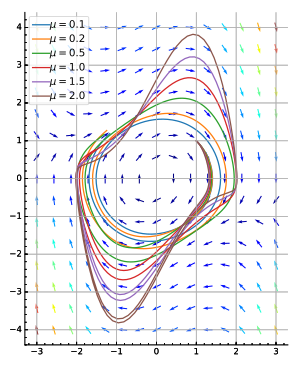
Un retrato de fase representa el comportamiento direccional de un sistema de ecuaciones diferenciales ordinarias (EDO). El retrato de fase puede indicar la estabilidad del sistema. ^[1]

El comportamiento del retrato de fase de un sistema de EDO puede determinarse mediante los valores propios o la traza y el determinante (traza = λ ₁ + λ ₂ , determinante = λ ₁ x λ ₂ ) del sistema. ^[1]

Ver también

• Espacio de fase
• Plano de fase

Referencias

1. Haynes Miller y Arthur Mattuck. 18.03 Ecuaciones diferenciales. Primavera de 2010. Instituto de Tecnología de Massachusetts: MIT OpenCourseWare, https://ocw.mit.edu. Licencia: Creative Commons BY-NC-SA. (Notas complementarias 26 de Haynes Miller: https://ocw.mit.edu/courses/18-03- Differential-equations-spring-2010/resources/mit18_03s10_chapter_26/)

• Jordania, DW; Smith, P. (2007). Ecuaciones diferenciales ordinarias no lineales (cuarta ed.). Prensa de la Universidad de Oxford. ISBN 978-0-19-920824-1.Capítulo 1.
• Steven Strogatz (2001). Dinámica No Lineal y Caos: Con aplicaciones a Física, Biología, Química e Ingeniería . ISBN 9780738204536.

enlaces externos

• Retratos de fase lineal, un MIT Mathlet.