La resistencia eléctrica de un objeto es una medida de su oposición al flujo de corriente eléctrica . Su cantidad recíproca esConductancia eléctrica , que mide la facilidad con la que pasa una corriente eléctrica. La resistencia eléctrica comparte algunos paralelismos conceptuales conla fricción. LaSIde resistencia eléctrica es elohmio( Ω ), mientras que la conductancia eléctrica se mide ensiemens(S) (antes llamado 'mho' y entonces representado por℧).
La resistencia de un objeto depende en gran medida del material del que está hecho. Los objetos hechos de aislantes eléctricos como el caucho tienden a tener una resistencia muy alta y una conductancia baja, mientras que los objetos hechos de conductores eléctricos como los metales tienden a tener una resistencia muy baja y una conductancia alta. Esta relación se cuantifica mediante la resistividad o la conductividad . Sin embargo, la naturaleza de un material no es el único factor en la resistencia y la conductancia; también depende del tamaño y la forma de un objeto porque estas propiedades son extensivas en lugar de intensivas . Por ejemplo, la resistencia de un cable es mayor si es largo y delgado, y menor si es corto y grueso. Todos los objetos resisten la corriente eléctrica, excepto los superconductores , que tienen una resistencia de cero.
La resistencia R de un objeto se define como la relación entre el voltaje V a través de él y la corriente I a través de él, mientras que la conductancia G es el recíproco:
Para una amplia variedad de materiales y condiciones, V e I son directamente proporcionales entre sí, y por lo tanto R y G son constantes (aunque dependerán del tamaño y la forma del objeto, del material del que está hecho y de otros factores como la temperatura o la tensión ). Esta proporcionalidad se denomina ley de Ohm , y los materiales que la satisfacen se denominan materiales óhmicos .
En otros casos, como en un transformador , un diodo o una batería , V e I no son directamente proporcionales. La relaciónV/I a veces sigue siendo útil y se denomina resistencia cordal o resistencia estática , [1] [2] ya que corresponde a la pendiente inversa de una cuerda entre el origen y una curva I – V. En otras situaciones, la derivada puede ser más útil; esto se llama resistencia diferencial .

En la analogía hidráulica , la corriente que fluye a través de un cable (o resistencia ) es como el agua que fluye a través de una tubería, y la caída de voltaje a través del cable es como la caída de presión que empuja el agua a través de la tubería. La conductancia es proporcional a la cantidad de flujo que se produce para una presión dada, y la resistencia es proporcional a la cantidad de presión que se requiere para lograr un flujo dado.
La caída de tensión (es decir, la diferencia entre las tensiones de un lado y del otro del resistor), no la tensión en sí, proporciona la fuerza impulsora que impulsa la corriente a través de un resistor. En hidráulica, es similar: la diferencia de presión entre dos lados de una tubería, no la presión en sí, determina el flujo a través de ella. Por ejemplo, puede haber una gran presión de agua por encima de la tubería, que intenta empujar el agua hacia abajo a través de ella, pero puede haber una presión de agua igualmente grande debajo de la tubería, que intenta empujar el agua hacia arriba a través de la tubería. Si estas presiones son iguales, no fluye agua. (En la imagen de la derecha, la presión del agua debajo de la tubería es cero).
La resistencia y la conductancia de un cable, resistor u otro elemento están determinadas principalmente por dos propiedades:
La geometría es importante porque es más difícil hacer pasar agua por una tubería larga y estrecha que por una tubería ancha y corta. De la misma manera, un cable de cobre largo y delgado tiene mayor resistencia (menor conductancia) que un cable de cobre corto y grueso.
Los materiales también son importantes. Una tubería llena de pelos restringe el flujo de agua más que una tubería limpia de la misma forma y tamaño. De manera similar, los electrones pueden fluir libre y fácilmente a través de un cable de cobre , pero no pueden fluir tan fácilmente a través de un cable de acero de la misma forma y tamaño, y esencialmente no pueden fluir en absoluto a través de un aislante como el caucho , independientemente de su forma. La diferencia entre el cobre, el acero y el caucho está relacionada con su estructura microscópica y configuración electrónica , y se cuantifica mediante una propiedad llamada resistividad .
Además de la geometría y el material, hay varios otros factores que influyen en la resistencia y la conductancia, como la temperatura; consulte a continuación.

Las sustancias por las que puede fluir la electricidad se denominan conductores . Una pieza de material conductor de una resistencia determinada destinada a utilizarse en un circuito se denomina resistencia . Los conductores están hechos de materiales de alta conductividad , como metales, en particular cobre y aluminio. Las resistencias, por otro lado, están hechas de una amplia variedad de materiales en función de factores como la resistencia deseada, la cantidad de energía que necesita disipar, la precisión y los costos.

En muchos materiales, la corriente I que pasa por el material es proporcional al voltaje V que se aplica a través de él: en un amplio rango de voltajes y corrientes. Por lo tanto, la resistencia y la conductancia de los objetos o componentes electrónicos hechos de estos materiales es constante. Esta relación se denomina ley de Ohm y los materiales que la obedecen se denominan materiales óhmicos . Algunos ejemplos de componentes óhmicos son los cables y las resistencias . El gráfico de corriente-voltaje de un dispositivo óhmico consiste en una línea recta que pasa por el origen con pendiente positiva .
Otros componentes y materiales utilizados en electrónica no obedecen la ley de Ohm; la corriente no es proporcional al voltaje, por lo que la resistencia varía con el voltaje y la corriente que pasan a través de ellos. Estos se denominan no lineales o no óhmicos . Algunos ejemplos son los diodos y las lámparas fluorescentes .

La resistencia de un objeto determinado depende principalmente de dos factores: el material del que está hecho y su forma. Para un material determinado, la resistencia es inversamente proporcional al área de la sección transversal; por ejemplo, un cable de cobre grueso tiene menor resistencia que un cable de cobre delgado idéntico en todo lo demás. Además, para un material determinado, la resistencia es proporcional a la longitud; por ejemplo, un cable de cobre largo tiene mayor resistencia que un cable de cobre corto idéntico en todo lo demás. Por lo tanto, la resistencia R y la conductancia G de un conductor de sección transversal uniforme se pueden calcular como
donde es la longitud del conductor, medida en metros (m), A es el área de la sección transversal del conductor medida en metros cuadrados (m 2 ), σ ( sigma ) es la conductividad eléctrica medida en siemens por metro (S·m −1 ), y ρ ( rho ) es la resistividad eléctrica (también llamada resistencia eléctrica específica ) del material, medida en ohmios-metros (Ω·m). La resistividad y la conductividad son constantes de proporcionalidad y, por lo tanto, dependen solo del material del que está hecho el cable, no de la geometría del cable. La resistividad y la conductividad son recíprocas : . La resistividad es una medida de la capacidad del material para oponerse a la corriente eléctrica.
Esta fórmula no es exacta, ya que supone que la densidad de corriente es totalmente uniforme en el conductor, lo que no siempre es cierto en situaciones prácticas. Sin embargo, esta fórmula aún proporciona una buena aproximación para conductores largos y delgados, como los cables.
Otra situación para la que esta fórmula no es exacta es con corriente alterna (CA), porque el efecto pelicular inhibe el flujo de corriente cerca del centro del conductor. Por esta razón, la sección transversal geométrica es diferente de la sección transversal efectiva en la que realmente fluye la corriente, por lo que la resistencia es mayor de lo esperado. De manera similar, si dos conductores cercanos entre sí transportan corriente CA, sus resistencias aumentan debido al efecto de proximidad . A la frecuencia de energía comercial , estos efectos son significativos para conductores grandes que transportan grandes corrientes, como barras colectoras en una subestación eléctrica , [3] o cables de energía grandes que transportan más de unos pocos cientos de amperios.
La resistividad de los distintos materiales varía enormemente: por ejemplo, la conductividad del teflón es aproximadamente 10 30 veces menor que la del cobre. En términos generales, esto se debe a que los metales tienen una gran cantidad de electrones "deslocalizados" que no están atrapados en ningún lugar, por lo que son libres de moverse a lo largo de grandes distancias. En un aislante, como el teflón, cada electrón está fuertemente ligado a una sola molécula, por lo que se requiere una gran fuerza para separarlo. Los semiconductores se encuentran entre estos dos extremos. Se pueden encontrar más detalles en el artículo: Resistividad eléctrica y conductividad . Para el caso de las soluciones electrolíticas , consulte el artículo: Conductividad (electrolítica) .
La resistividad varía con la temperatura. En los semiconductores, la resistividad también cambia cuando se expone a la luz. Véase a continuación.

Un instrumento para medir la resistencia se llama ohmímetro . Los ohmímetros simples no pueden medir resistencias bajas con precisión porque la resistencia de sus cables de medición provoca una caída de voltaje que interfiere con la medición, por lo que los dispositivos más precisos utilizan detección de cuatro terminales .
Muchos elementos eléctricos, como los diodos y las baterías , no cumplen la ley de Ohm . Se denominan no óhmicos o no lineales y sus curvas de corriente-voltaje no son líneas rectas que pasan por el origen.
La resistencia y la conductancia también se pueden definir para elementos no óhmicos. Sin embargo, a diferencia de la resistencia óhmica, la resistencia no lineal no es constante, sino que varía con el voltaje o la corriente a través del dispositivo; es decir, su punto de operación . Existen dos tipos de resistencia: [1] [2]
Esto corresponde a la definición habitual de resistencia: el voltaje dividido por la corriente.
Es la pendiente de la línea ( cuerda ) desde el origen a través del punto en la curva. La resistencia estática determina la disipación de potencia en un componente eléctrico. Los puntos en la curva de corriente-voltaje ubicados en el 2º o 4º cuadrante, para los cuales la pendiente de la línea de cuerda es negativa, tienen resistencia estática negativa . Los dispositivos pasivos , que no tienen fuente de energía, no pueden tener resistencia estática negativa. Sin embargo, los dispositivos activos como transistores o amplificadores operacionales pueden sintetizar resistencia estática negativa con retroalimentación, y se usa en algunos circuitos como los giradores .Es la derivada del voltaje con respecto a la corriente; la pendiente de la curva corriente-voltaje en un punto
Si la curva de corriente-voltaje no es monótona (con picos y valles), la curva tiene una pendiente negativa en algunas regiones, por lo que en estas regiones el dispositivo tiene una resistencia diferencial negativa . Los dispositivos con resistencia diferencial negativa pueden amplificar una señal que se les aplica y se utilizan para fabricar amplificadores y osciladores. Estos incluyen diodos túnel , diodos Gunn , diodos IMPATT , tubos de magnetrón y transistores unijuntura .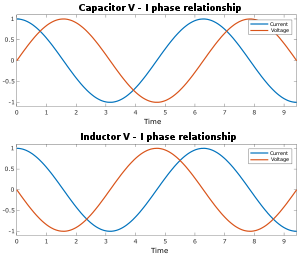
Cuando una corriente alterna fluye a través de un circuito, la relación entre la corriente y el voltaje a través de un elemento del circuito se caracteriza no solo por la relación de sus magnitudes, sino también por la diferencia en sus fases . Por ejemplo, en un resistor ideal , en el momento en que el voltaje alcanza su máximo, la corriente también alcanza su máximo (la corriente y el voltaje oscilan en fase). Pero para un capacitor o inductor , el flujo máximo de corriente ocurre cuando el voltaje pasa por cero y viceversa (la corriente y el voltaje oscilan 90° fuera de fase, vea la imagen a continuación). Los números complejos se utilizan para realizar un seguimiento tanto de la fase como de la magnitud de la corriente y el voltaje:
dónde:
La impedancia y la admitancia pueden expresarse como números complejos que pueden descomponerse en partes reales e imaginarias:
donde R es resistencia, G es conductancia, X es reactancia y B es susceptancia . Estos conducen a las identidades de números complejos que son verdaderas en todos los casos, mientras que solo es verdadera en los casos especiales de corriente continua o sin reactancia.
El ángulo complejo es la diferencia de fase entre el voltaje y la corriente que pasan a través de un componente con impedancia Z. Para capacitores e inductores , este ángulo es exactamente -90° o +90°, respectivamente, y X y B son distintos de cero. Los resistores ideales tienen un ángulo de 0°, ya que X es cero (y por lo tanto B también), y Z e Y se reducen a R y G respectivamente. En general, los sistemas de CA están diseñados para mantener el ángulo de fase cerca de 0° tanto como sea posible, ya que reduce la potencia reactiva , que no realiza ningún trabajo útil en una carga. En un caso simple con una carga inductiva (que hace que la fase aumente), se puede agregar un capacitor para compensación en una frecuencia, ya que el cambio de fase del capacitor es negativo, lo que acerca la fase de impedancia total nuevamente a 0°.
Y es el recíproco de Z ( ) para todos los circuitos, al igual que para los circuitos de CC que contienen solo resistencias, o circuitos de CA para los cuales la reactancia o la susceptancia son cero ( X o B = 0 , respectivamente) (si uno es cero, entonces para sistemas realistas ambos deben ser cero).
Una característica clave de los circuitos de CA es que la resistencia y la conductancia pueden depender de la frecuencia, un fenómeno conocido como respuesta dieléctrica universal . [8] Una razón, mencionada anteriormente, es el efecto pelicular (y el efecto de proximidad relacionado ). Otra razón es que la resistividad en sí misma puede depender de la frecuencia (ver modelo de Drude , trampas de nivel profundo , frecuencia resonante , relaciones de Kramers-Kronig , etc.)

Los resistores (y otros elementos con resistencia) se oponen al flujo de corriente eléctrica; por lo tanto, se requiere energía eléctrica para impulsar la corriente a través de la resistencia. Esta energía eléctrica se disipa, calentando el resistor en el proceso. Esto se llama calentamiento Joule (en honor a James Prescott Joule ), también llamado calentamiento óhmico o calentamiento resistivo .
La disipación de energía eléctrica es a menudo indeseable, en particular en el caso de pérdidas de transmisión en líneas eléctricas . La transmisión de alta tensión ayuda a reducir las pérdidas al reducir la corriente para una potencia determinada.
Por otro lado, el calentamiento Joule es a veces útil, por ejemplo, en estufas eléctricas y otros calentadores eléctricos (también llamados calentadores resistivos ). Como otro ejemplo, las lámparas incandescentes se basan en el calentamiento Joule: el filamento se calienta a una temperatura tan alta que brilla "al rojo vivo" con radiación térmica (también llamada incandescencia ).
La fórmula para el calentamiento Joule es: donde P es la potencia (energía por unidad de tiempo) convertida de energía eléctrica a energía térmica, R es la resistencia e I es la corriente a través de la resistencia.
Cerca de la temperatura ambiente, la resistividad de los metales generalmente aumenta a medida que aumenta la temperatura, mientras que la resistividad de los semiconductores generalmente disminuye a medida que aumenta la temperatura. La resistividad de los aislantes y electrolitos puede aumentar o disminuir según el sistema. Para conocer el comportamiento y la explicación detallados, consulte Resistividad y conductividad eléctricas .
Como consecuencia, la resistencia de cables, resistencias y otros componentes suele cambiar con la temperatura. Este efecto puede ser indeseado y provocar que un circuito electrónico funcione mal a temperaturas extremas. Sin embargo, en algunos casos, el efecto se aprovecha de forma adecuada. Cuando se utiliza de forma intencionada la resistencia dependiente de la temperatura de un componente, el componente se denomina termómetro de resistencia o termistor . (Un termómetro de resistencia está hecho de metal, normalmente platino, mientras que un termistor está hecho de cerámica o polímero).
Los termómetros de resistencia y los termistores se utilizan generalmente de dos maneras. En primer lugar, se pueden utilizar como termómetros : midiendo la resistencia, se puede inferir la temperatura del entorno. En segundo lugar, se pueden utilizar junto con el calentamiento Joule (también llamado autocalentamiento): si una gran corriente circula por la resistencia, la temperatura de la resistencia aumenta y, por lo tanto, su resistencia cambia. Por lo tanto, estos componentes se pueden utilizar en una función de protección de circuitos similar a los fusibles , o para retroalimentación en circuitos, o para muchos otros fines. En general, el autocalentamiento puede convertir una resistencia en un elemento de circuito no lineal e histéresis . Para obtener más detalles, consulte Termistor#Efectos del autocalentamiento .
Si la temperatura T no varía demasiado, se suele utilizar una aproximación lineal : donde se denomina coeficiente de temperatura de resistencia , es una temperatura de referencia fija (normalmente la temperatura ambiente) y es la resistencia a la temperatura . El parámetro es un parámetro empírico ajustado a partir de datos de medición. Como la aproximación lineal es solo una aproximación, es diferente para diferentes temperaturas de referencia. Por este motivo, es habitual especificar la temperatura a la que se midió con un sufijo, como , y la relación solo se cumple en un rango de temperaturas alrededor de la referencia. [9]
El coeficiente de temperatura es típicamente+3 × 10 −3 K−1 a+6 × 10 −3 K−1 para metales cerca de la temperatura ambiente. Suele ser negativo para semiconductores y aislantes, con una magnitud muy variable. [e]
Así como la resistencia de un conductor depende de la temperatura, la resistencia de un conductor depende de la deformación . [10] Al colocar un conductor bajo tensión (una forma de estrés que conduce a una deformación en forma de estiramiento del conductor), la longitud de la sección del conductor bajo tensión aumenta y su área de sección transversal disminuye. Ambos efectos contribuyen a aumentar la resistencia de la sección deformada del conductor. Bajo compresión (deformación en la dirección opuesta), la resistencia de la sección deformada del conductor disminuye. Consulte la discusión sobre los medidores de tensión para obtener detalles sobre los dispositivos construidos para aprovechar este efecto.
Algunas resistencias, en particular las fabricadas a partir de semiconductores , presentan fotoconductividad , lo que significa que su resistencia cambia cuando la luz incide sobre ellas. Por lo tanto, se denominan fotorresistores (o resistencias dependientes de la luz ). Son un tipo común de detector de luz .
Los superconductores son materiales que tienen una resistencia exactamente cero y una conductancia infinita, porque pueden tener V = 0 e I ≠ 0. Esto también significa que no hay calentamiento Joule , o en otras palabras, no hay disipación de energía eléctrica. Por lo tanto, si se hace un bucle cerrado con un cable superconductor, la corriente fluye por el bucle para siempre. Los superconductores requieren enfriamiento a temperaturas cercanas4 K con helio líquido para la mayoría de los superconductores metálicos como las aleaciones de niobio y estaño , o enfriamiento a temperaturas cercanas77 K con nitrógeno líquido para los costosos, frágiles y delicados superconductores cerámicos de alta temperatura . Sin embargo, existen muchas aplicaciones tecnológicas de la superconductividad , incluidos los imanes superconductores .