
En la teoría de decisiones , una regla de puntuación [1] proporciona métricas de evaluación para predicciones o pronósticos probabilísticos . Mientras que las funciones de pérdida "regulares" (como el error cuadrático medio ) asignan una puntuación de bondad de ajuste a un valor predicho y a un valor observado, las reglas de puntuación asignan dicha puntuación a una distribución de probabilidad predicha y a un valor observado. Por otro lado, una función de puntuación [2] proporciona una medida de resumen para la evaluación de predicciones puntuales, es decir, se predice una propiedad o una función , como la expectativa o la mediana .


Las reglas de puntuación tienen como objetivo responder a la pregunta "¿qué tan buena es una distribución de probabilidad predicha en comparación con una observación?" Una propiedad importante de las reglas de puntuación es la propiedad (estricta) . En esencia, se ha demostrado que las reglas de puntuación (estrictamente) adecuadas tienen la puntuación esperada más baja si la distribución predicha es igual a la distribución subyacente de la variable objetivo. Aunque esto puede diferir para las observaciones individuales, debería dar como resultado una minimización de la puntuación esperada si se predicen las distribuciones "correctas".
Las reglas de puntuación y las funciones de puntuación se utilizan a menudo como "funciones de costo" o " funciones de pérdida " de los modelos de pronóstico probabilísticos. Se evalúan como la media empírica de una muestra dada, la "puntuación". Las puntuaciones de diferentes predicciones o modelos se pueden comparar para concluir qué modelo es mejor. Por ejemplo, considere un modelo que predice (basado en una entrada ) una media y una desviación estándar . Juntas, esas variables definen una distribución gaussiana , en esencia, prediciendo la variable objetivo como una distribución de probabilidad. Una interpretación común de los modelos probabilísticos es que apuntan a cuantificar su propia incertidumbre predictiva. En este ejemplo, una variable objetivo observada se compara con la distribución predicha y se le asigna una puntuación . Al entrenar con una regla de puntuación, debe "enseñar" a un modelo probabilístico a predecir cuándo su incertidumbre es baja y cuándo su incertidumbre es alta, y debe dar como resultado predicciones calibradas , al tiempo que minimiza la incertidumbre predictiva.
Aunque el ejemplo dado se refiere a la predicción probabilística de una variable objetivo con valor real , se han diseñado diversas reglas de puntuación diferentes, teniendo en cuenta distintas variables objetivo. Existen reglas de puntuación para la clasificación probabilística binaria y categórica , así como para la regresión probabilística univariante y multivariante .
Consideremos un espacio muestral , una σ-álgebra de subconjuntos de y una clase convexa de medidas de probabilidad en . Una función definida en y que toma valores en la recta real extendida, , es -cuasiintegrable si es medible con respecto a y es cuasiintegrable con respecto a todos los .
Un pronóstico probabilístico es cualquier medida de probabilidad , es decir, es una distribución de posibles observaciones futuras.
Una regla de puntuación es cualquier función de valor real extendida tal que sea -cuasi-integrable para todos los . representa la pérdida o penalización cuando se emite el pronóstico y la observación se materializa .
Un pronóstico puntual es una función, es decir, un mapeo potencialmente valorado .
Una función de puntuación es cualquier función de valor real donde representa la pérdida o penalización cuando se emite el pronóstico de puntos y se materializa la observación.
Las reglas y funciones de puntuación tienen una orientación negativa (positiva) si los valores más pequeños (más grandes) significan que es mejor. En este caso, nos adherimos a la orientación negativa, de ahí la asociación con "pérdida".
Escribimos para el puntaje esperado de una predicción bajo como el puntaje esperado de la distribución predicha , al muestrear observaciones de la distribución .
Muchos modelos de pronóstico probabilístico se entrenan a través del puntaje promedio de la muestra, en el que se evalúa un conjunto de distribuciones predichas frente a un conjunto de observaciones .
Las reglas de puntuación estrictamente adecuadas y las funciones de puntuación estrictamente consistentes fomentan los pronósticos honestos mediante la maximización de la recompensa esperada: si a un pronosticador se le da una recompensa de si realiza (por ejemplo, ), entonces la recompensa esperada más alta (puntuación más baja) se obtiene al informar la distribución de probabilidad real. [1]
Una regla de puntuación es adecuada en relación con si (asumiendo una orientación negativa) su puntuación esperada se minimiza cuando la distribución prevista coincide con la distribución de la observación.
Es estrictamente apropiado si la ecuación anterior se cumple con igualdad si y sólo si .
Una función de puntuación es consistente para el funcional en relación con la clase si
Es estrictamente consistente si es consistente y la igualdad en la ecuación anterior implica que .

Un ejemplo de pronóstico probabilístico es la meteorología, donde un pronosticador del tiempo puede dar la probabilidad de lluvia al día siguiente. Se podría anotar el número de veces que se citó una probabilidad del 25%, durante un largo período, y compararla con la proporción real de veces que cayó lluvia. Si el porcentaje real fue sustancialmente diferente de la probabilidad declarada, decimos que el pronosticador está mal calibrado . Un pronosticador mal calibrado podría verse alentado a hacerlo mejor mediante un sistema de bonificación. Un sistema de bonificación diseñado en torno a una regla de puntuación adecuada incentivará al pronosticador a informar probabilidades iguales a sus creencias personales . [3]
Además del caso simple de una decisión binaria , como asignar probabilidades a "lluvia" o "no lluvia", se pueden usar reglas de puntuación para múltiples clases, como "lluvia", "nieve" o "claro", o respuestas continuas como la cantidad de lluvia por día.
La imagen de la derecha muestra un ejemplo de una regla de puntuación, la regla de puntuación logarítmica, en función de la probabilidad informada para el evento que realmente ocurrió. Una forma de utilizar esta regla sería como un costo basado en la probabilidad que asigna un pronosticador o un algoritmo y luego verifica qué evento ocurre realmente.
Existe una cantidad infinita de reglas de puntuación, incluidas familias enteras parametrizadas de reglas de puntuación estrictamente adecuadas. Las que se muestran a continuación son simplemente ejemplos populares.
Para una variable de respuesta categórica con eventos mutuamente excluyentes, un pronosticador o algoritmo probabilístico devolverá un vector de probabilidad con una probabilidad para cada uno de los resultados.
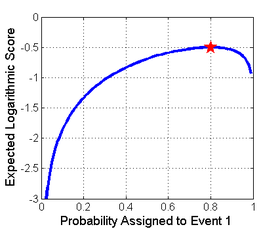
La regla de puntuación logarítmica es una regla de puntuación local estrictamente propia. También es la contraparte de " sorpresa" , que se utiliza comúnmente como criterio de puntuación en la inferencia bayesiana ; el objetivo es minimizar la sorpresa esperada. Esta regla de puntuación tiene fundamentos sólidos en la teoría de la información .
Aquí, la puntuación se calcula como el logaritmo de la estimación de probabilidad para el resultado real. Es decir, una predicción del 80% que resultó ser correcta recibiría una puntuación de ln(0,8) = −0,22 . Esta misma predicción también asigna una probabilidad del 20% al caso opuesto, por lo que si la predicción resulta falsa, recibiría una puntuación basada en el 20%: ln(0,2) = −1,6 . El objetivo de un pronosticador es maximizar la puntuación y que esta sea lo más alta posible, y −0,22 es de hecho mayor que −1,6.
Si se considera la verdad o falsedad de la predicción como una variable x con valor 1 o 0 respectivamente, y la probabilidad expresada como p , entonces se puede escribir la regla de puntuación logarítmica como x ln( p ) + (1 − x ) ln(1 − p ) . Nótese que se puede utilizar cualquier base logarítmica, ya que las reglas de puntuación estrictamente adecuadas siguen siendo estrictamente adecuadas bajo una transformación lineal. Es decir:
es estrictamente apropiado para todos .
La regla de puntuación cuadrática es una regla de puntuación estrictamente adecuada
donde es la probabilidad asignada a la respuesta correcta y es el número de clases.
La puntuación Brier , propuesta originalmente por Glenn W. Brier en 1950, [4] se puede obtener mediante una transformación afín de la regla de puntuación cuadrática.
Donde cuando el evento th es correcto y en caso contrario y es el número de clases.
Una diferencia importante entre estas dos reglas es que el pronosticador debe esforzarse por maximizar la puntuación cuadrática y minimizar la puntuación de Brier . Esto se debe a un signo negativo en la transformación lineal entre ellas.
La función de puntuación de Hyvärinen (de una densidad p) está definida por [5]
Donde denota la traza hessiana y denota el gradiente . Esta regla de puntuación se puede utilizar para simplificar computacionalmente la inferencia de parámetros y abordar la comparación de modelos bayesianos con valores previos arbitrariamente vagos. [5] [6] También se utilizó para introducir nuevas cantidades de teoría de la información más allá de la teoría de la información existente . [7]
La regla de puntuación esférica también es una regla de puntuación estrictamente adecuada.
La puntuación de probabilidad clasificada [8] (RPS) es una regla de puntuación estrictamente adecuada, que se puede expresar como:
Donde cuando el evento th es correcto y en caso contrario, y es el número de clases. Aparte de otras reglas de puntuación, la puntuación de probabilidad clasificada considera la distancia entre clases, es decir, las clases 1 y 2 se consideran más cercanas que las clases 1 y 3. La puntuación asigna mejores puntuaciones a los pronósticos probabilísticos con altas probabilidades asignadas a clases cercanas a la clase correcta. Por ejemplo, al considerar los pronósticos probabilísticos y , encontramos que , mientras que , a pesar de que ambos pronósticos probabilísticos asignan una probabilidad idéntica a la clase correcta.
A continuación, a la izquierda, se muestra una comparación gráfica de las reglas de puntuación logarítmica, cuadrática y esférica para un problema de clasificación binaria. El eje x indica la probabilidad informada del evento que realmente ocurrió.
Es importante señalar que cada una de las puntuaciones tiene magnitudes y ubicaciones diferentes. Sin embargo, las diferencias de magnitud no son relevantes, ya que las puntuaciones siguen siendo adecuadas bajo una transformación afín. Por lo tanto, para comparar diferentes puntuaciones es necesario trasladarlas a una escala común. Una opción razonable de normalización se muestra en la imagen de la derecha, donde todas las puntuaciones intersecan los puntos (0,5, 0) y (1, 1). Esto garantiza que arrojen 0 para una distribución uniforme (dos probabilidades de 0,5 cada una), lo que no refleja ningún coste ni recompensa por informar lo que suele ser la distribución de referencia. Todas las puntuaciones normalizadas que aparecen a continuación también arrojan 1 cuando a la clase real se le asigna una probabilidad de 1.
Las reglas de puntuación que se enumeran a continuación tienen como objetivo evaluar las predicciones probabilísticas cuando las distribuciones predichas son distribuciones de probabilidad continuas univariadas , es decir, las distribuciones predichas se definen sobre una variable objetivo univariada y tienen una función de densidad de probabilidad .
La puntuación logarítmica es una regla de puntuación local estrictamente propia. Se define como
donde denota la función de densidad de probabilidad de la distribución predicha . Es una regla de puntuación local estrictamente apropiada. La puntuación logarítmica para variables continuas tiene fuertes vínculos con la estimación de máxima verosimilitud . Sin embargo, en muchas aplicaciones, la puntuación de probabilidad clasificada continua a menudo se prefiere sobre la puntuación logarítmica, ya que la puntuación logarítmica puede verse muy influenciada por ligeras desviaciones en las densidades de cola de las distribuciones pronosticadas. [9]

La puntuación de probabilidad clasificada continua (CRPS) [10] es una regla de puntuación estrictamente adecuada que se utiliza mucho en meteorología. Se define como
donde es la función de distribución acumulativa de la distribución prevista , es la función de paso de Heaviside y es la observación. Para distribuciones con un primer momento finito, la puntuación de probabilidad clasificada continua se puede escribir como: [1]
donde y son variables aleatorias independientes, muestreadas de la distribución . Además, cuando la función de probabilidad acumulada es continua, la puntuación de probabilidad clasificada continua también se puede escribir como [11]
La puntuación de probabilidad clasificada continua puede considerarse tanto una extensión continua de la puntuación de probabilidad clasificada como una regresión cuantil . La puntuación de probabilidad clasificada continua sobre la distribución empírica de un conjunto ordenado de puntos (es decir, cada punto tiene probabilidad de ocurrir), es igual al doble de la pérdida cuantil media aplicada en aquellos puntos con cuantiles distribuidos uniformemente : [12]
Para muchas familias populares de distribuciones, se han derivado expresiones de forma cerrada para la puntuación de probabilidad clasificada continua. La puntuación de probabilidad clasificada continua se ha utilizado como una función de pérdida para redes neuronales artificiales , en las que los pronósticos meteorológicos se posprocesan a una distribución de probabilidad gaussiana . [13] [14]
El CRPS también se adaptó al análisis de supervivencia para cubrir eventos censurados. [15]
Las reglas de puntuación que se enumeran a continuación tienen como objetivo evaluar las predicciones probabilísticas cuando las distribuciones predichas son distribuciones de probabilidad continuas univariadas , es decir, las distribuciones predichas se definen sobre una variable objetivo multivariada y tienen una función de densidad de probabilidad .
La puntuación logarítmica multivariada es similar a la puntuación logarítmica univariante:
donde denota la función de densidad de probabilidad de la distribución multivariante predicha . Es una regla de puntuación local estrictamente apropiada.
La puntuación energética es una extensión multivariada de la puntuación de probabilidad clasificada continua: [1]
Aquí, , denota la distancia euclidiana -dimensional y son variables aleatorias muestreadas independientemente de la distribución de probabilidad . El puntaje de energía es estrictamente apropiado para distribuciones para las cuales es finito. Se ha sugerido que el puntaje de energía es algo ineficaz al evaluar la estructura de dependencia intervariable de la distribución multivariada pronosticada. [16] El puntaje de energía es igual al doble de la distancia de energía entre la distribución predicha y la distribución empírica de la observación.
La puntuación del orden del variograma viene dada por: [17]
Aquí, se encuentran los pesos, que a menudo se establecen en 1, y se pueden elegir de forma arbitraria, pero a menudo se utilizan o . está aquí para indicar la variable aleatoria marginal 'ésima de . La puntuación del variograma es adecuada para distribuciones para las que el momento 'ésimo es finito para todos los componentes, pero nunca es estrictamente adecuada. En comparación con la puntuación de energía, se afirma que la puntuación del variograma es más discriminativa con respecto a la estructura de correlación predicha.
La puntuación de probabilidad condicional continua clasificada (CRPS condicional o CCRPS) es una familia de reglas de puntuación (estrictamente) adecuadas. La CRPS condicional evalúa una distribución multivariada prevista mediante la evaluación de la CRPS sobre un conjunto prescrito de distribuciones de probabilidad condicional univariadas de la distribución multivariada prevista: [18]
Aquí, es la 'ésima variable marginal de , es un conjunto de tuplas que define una especificación condicional (con y ), y denota la distribución de probabilidad condicional para dado que todas las variables para son iguales a sus respectivas observaciones. En el caso de que esté mal definido (es decir, su evento condicional tiene probabilidad cero), las puntuaciones CRPS sobre esta distribución se definen como infinitas. La CRPS condicional es estrictamente apropiada para distribuciones con primer momento finito, si la regla de la cadena está incluida en la especificación condicional, lo que significa que existe una permutación de tal que para todo : .
Todas las reglas de puntuación adecuadas son iguales a sumas ponderadas (integrales con una función de ponderación no negativa) de las pérdidas en un conjunto de problemas de decisión simples de dos alternativas que utilizan la predicción probabilística, cada uno de esos problemas de decisión tiene una combinación particular de parámetros de costo asociados para decisiones de falsos positivos y falsos negativos . Una regla de puntuación estrictamente adecuada corresponde a tener una ponderación distinta de cero para todos los umbrales de decisión posibles. Cualquier regla de puntuación adecuada dada es igual a las pérdidas esperadas con respecto a una distribución de probabilidad particular sobre los umbrales de decisión; por lo tanto, la elección de una regla de puntuación corresponde a un supuesto sobre la distribución de probabilidad de los problemas de decisión para los que se emplearán en última instancia las probabilidades predichas, con, por ejemplo, la regla de puntuación de pérdida cuadrática (o Brier) correspondiente a una probabilidad uniforme de que el umbral de decisión esté en cualquier lugar entre cero y uno. La puntuación de precisión de la clasificación (porcentaje de clasificados correctamente), una regla de puntuación de umbral único que es cero o uno dependiendo de si la probabilidad predicha está en el lado apropiado de 0,5, es una regla de puntuación adecuada pero no estrictamente adecuada porque está optimizada (en expectativa) no solo al predecir la probabilidad real sino al predecir cualquier probabilidad en el mismo lado de 0,5 que la probabilidad real. [19] [20] [21] [22] [23] [24]
Una regla de puntuación estrictamente adecuada, ya sea binaria o multiclase, después de una transformación afín sigue siendo una regla de puntuación estrictamente adecuada. [3] Es decir, si es una regla de puntuación estrictamente adecuada, entonces con también es una regla de puntuación estrictamente adecuada, aunque si entonces el sentido de optimización de la regla de puntuación cambia entre maximización y minimización.
Se dice que una regla de puntuación adecuada es local si su estimación de la probabilidad de un evento específico depende únicamente de la probabilidad de ese evento. Esta afirmación es vaga en la mayoría de las descripciones, pero en la mayoría de los casos podemos pensar en esto como que la solución óptima del problema de puntuación "en un evento específico" es invariable a todos los cambios en la distribución de observaciones que dejan la probabilidad de ese evento sin cambios. Todas las puntuaciones binarias son locales porque la probabilidad asignada al evento que no ocurrió está determinada, por lo que no hay ningún grado de flexibilidad para variar.
Las funciones afines de la regla de puntuación logarítmica son las únicas reglas de puntuación locales estrictamente adecuadas en un conjunto finito que no es binario.
El valor esperado de una regla de puntuación adecuada se puede descomponer en la suma de tres componentes, llamados incertidumbre , confiabilidad y resolución , [25] [26] que caracterizan diferentes atributos de los pronósticos probabilísticos:
Si una puntuación es adecuada y de orientación negativa (como la puntuación Brier), los tres términos son definidos positivos. El componente de incertidumbre es igual a la puntuación esperada del pronóstico que predice constantemente la frecuencia media de los eventos. El componente de fiabilidad penaliza los pronósticos mal calibrados, en los que las probabilidades predichas no coinciden con las frecuencias de los eventos.
Las ecuaciones para los componentes individuales dependen de la regla de puntuación particular. Para la puntuación Brier, se dan por
donde es la probabilidad media de ocurrencia del evento binario , y es la probabilidad condicional del evento, dada , es decir