En la filosofía de las matemáticas , el realismo aristotélico sostiene que las matemáticas estudian propiedades como la simetría , la continuidad y el orden que pueden realizarse de manera inmanente en el mundo físico (o en cualquier otro mundo que pudiera existir). Contrasta con el platonismo al sostener que los objetos de las matemáticas, como los números, no existen en un mundo "abstracto" sino que pueden realizarse físicamente. [1] Contrasta con el nominalismo , el ficcionalismo y el logicismo al sostener que las matemáticas no tratan de meros nombres o métodos de inferencia o cálculo sino de ciertos aspectos reales del mundo.
Los realistas aristotélicos enfatizan las matemáticas aplicadas , especialmente el modelado matemático , en lugar de las matemáticas puras como filosóficamente más importantes. Marc Lange sostiene que "el realismo aristotélico permite que los hechos matemáticos sean explicaciones distintivamente matemáticas" en la ciencia, ya que los hechos matemáticos en sí mismos tratan sobre el mundo físico. [2] Paul Thagard describe el realismo aristotélico como "la filosofía actual de las matemáticas que se ajusta mejor a lo que se sabe sobre las mentes y la ciencia ". [3]
Aunque Aristóteles no escribió extensamente sobre la filosofía de las matemáticas, sus diversas observaciones sobre el tema muestran una visión coherente del tema como algo que trata tanto de abstracciones como de su aplicación al mundo real del espacio y el conteo. [4] Hasta el siglo XVIII, la filosofía más común de las matemáticas era la visión aristotélica de que es la "ciencia de la cantidad ", con la cantidad dividida en continua (estudiada por la geometría ) y discreta (estudiada por la aritmética). [5]
Los enfoques aristotélicos de la filosofía de las matemáticas fueron raros en el siglo XX, pero fueron revividos por Penelope Maddy en Realism in Mathematics (1990) y por varios autores desde 2000, como James Franklin , [6] Anne Newstead, [7] Donald Gillies y otros.
Las visiones aristotélicas de los números ( cardinales o de conteo) comienzan con la observación de Aristóteles de que el número de un montón o colección es relativo a la unidad o medida elegida: "'número' significa una pluralidad medida y una pluralidad de medidas... la medida debe ser siempre algo idéntico predicable de todas las cosas que mide, por ejemplo, si las cosas son caballos, la medida es 'caballo'". [8] Glenn Kessler desarrolla esto en la visión de que un número es una relación entre un montón y un universal que lo divide en unidades; por ejemplo, el número 4 se realiza en la relación entre un montón de loros y el universal "ser un loro" que divide el montón en tantos loros. [9] [10] [5] : 36–8
Desde el punto de vista aristotélico, las razones no están estrechamente relacionadas con los números cardinales. Son relaciones entre cantidades, como las alturas. Una razón entre dos alturas puede ser la misma que la relación entre dos masas o dos intervalos de tiempo. [5] : 34–5
Los aristotélicos consideran que los conjuntos, así como los números, están instanciados en el mundo físico (en lugar de ser entidades platónicas). Maddy sostuvo que cuando se abre un cartón de huevos, se percibe un conjunto de tres huevos (es decir, una entidad matemática realizada en el mundo físico). [11] Sin embargo, no todo el discurso matemático necesita ser interpretado de manera realista; por ejemplo, los aristotélicos pueden considerar el conjunto vacío y el cero como ficciones, [5] : 234–40 y posiblemente infinitos superiores.
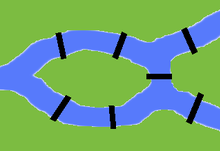
Los aristotélicos consideran que las propiedades estructurales no numéricas, como la simetría, la continuidad y el orden, son tan importantes como los números. Dichas propiedades se realizan en la realidad física y son objeto de estudio de partes de las matemáticas. Por ejemplo, la teoría de grupos clasifica los diferentes tipos de simetría, mientras que el cálculo estudia la variación continua. Los resultados demostrables sobre dichas estructuras pueden aplicarse directamente a la realidad física. Por ejemplo, Euler demostró que era imposible caminar una sola vez sobre los siete puentes de Königsberg . [5] : 48–56
Dado que las propiedades matemáticas se materializan en el mundo físico, se pueden percibir directamente. Por ejemplo, los humanos percibimos fácilmente la simetría facial .
Los aristotélicos también conceden un papel a la abstracción y la idealización en el pensamiento matemático. Esta visión se remonta a la afirmación de Aristóteles en su Física de que la mente "separa" en el pensamiento las propiedades que estudia en matemáticas, considerando las propiedades atemporales de los cuerpos al margen del mundo del cambio (Física II.2.193b31-35).
En los niveles superiores de las matemáticas, los aristotélicos siguen la teoría de los Analíticos Posteriores de Aristóteles , según la cual la prueba de una proposición matemática permite idealmente al lector entender por qué la proposición debe ser verdadera. [5] : 192–6
Un problema para el realismo aristotélico es qué explicación dar a los infinitos superiores , que pueden no realizarse o no ser realizables en el mundo físico. Mark Balaguer escribe:
Los aristotélicos responden que las ciencias pueden tratar con universales no instanciados; por ejemplo, la ciencia del color puede tratar con un tono de azul que no se da en ningún objeto real. [13] Sin embargo, eso requiere negar el principio de instanciación , sostenido por la mayoría de los aristotélicos, que sostiene que todas las propiedades genuinas son instanciadas. Un filósofo aristotélico de las matemáticas que niega el principio de instanciación sobre la base de la distinción de Frege entre sentido y referencia es Donald Gillies . Ha utilizado este enfoque para desarrollar un método para tratar con cardinales transfinitos muy grandes desde un punto de vista aristotélico. [14]
Otra objeción al aristotelismo es que las matemáticas se ocupan de idealizaciones del mundo físico, no del mundo físico en sí. El propio Aristóteles era consciente del argumento de que los geómetras estudian círculos perfectos, pero los aros del mundo real no son círculos perfectos, por lo que parece que las matemáticas deben estar estudiando algún mundo no físico (platónico). [15] Los aristotélicos responden que las matemáticas aplicadas estudian aproximaciones en lugar de idealizaciones y que, como resultado, las matemáticas modernas pueden estudiar las formas complejas y otras estructuras matemáticas de las cosas reales. [5] : 225–9 [16]