Diseño de proteínas

Diseño racional de nuevas moléculas de proteínas

El diseño de proteínas es el diseño racional de nuevas moléculas de proteínas para diseñar una actividad, un comportamiento o un propósito novedosos y para avanzar en la comprensión básica de la función de las proteínas. ^[1] Las proteínas se pueden diseñar desde cero ( diseño de novo ) o haciendo variantes calculadas de una estructura proteica conocida y su secuencia (denominado rediseño de proteínas ). Los enfoques de diseño de proteínas racionales hacen predicciones de secuencias de proteínas que se plegarán a estructuras específicas. Estas secuencias predichas se pueden validar experimentalmente a través de métodos como la síntesis de péptidos , la mutagénesis dirigida al sitio o la síntesis artificial de genes .

El diseño racional de proteínas se remonta a mediados de la década de 1970. ^[2] Sin embargo, recientemente ha habido numerosos ejemplos de diseño racional exitoso de péptidos y proteínas solubles en agua e incluso transmembrana, en parte debido a una mejor comprensión de los diferentes factores que contribuyen a la estabilidad de la estructura de las proteínas y al desarrollo de mejores métodos computacionales.

Visión general e historia

El objetivo del diseño racional de proteínas es predecir las secuencias de aminoácidos que se plegarán hasta una estructura proteica específica. Aunque el número de posibles secuencias proteicas es enorme y crece exponencialmente con el tamaño de la cadena proteica, solo un subconjunto de ellas se plegará de forma fiable y rápida hasta un estado nativo . El diseño de proteínas implica la identificación de secuencias nuevas dentro de este subconjunto. El estado nativo de una proteína es el mínimo de energía libre conformacional de la cadena. Por tanto, el diseño de proteínas es la búsqueda de secuencias que tengan la estructura elegida como mínimo de energía libre. En cierto sentido, es lo inverso de la predicción de la estructura de las proteínas . En el diseño, se especifica una estructura terciaria y se identifica una secuencia que se plegará hasta ella. Por tanto, también se denomina plegamiento inverso . El diseño de proteínas es entonces un problema de optimización: utilizando algunos criterios de puntuación, se elige una secuencia optimizada que se plegará hasta la estructura deseada.

Cuando se diseñaron racionalmente las primeras proteínas durante los años 1970 y 1980, la secuencia de estas se optimizó manualmente basándose en análisis de otras proteínas conocidas, la composición de la secuencia, las cargas de aminoácidos y la geometría de la estructura deseada. ^[2] Las primeras proteínas diseñadas se atribuyen a Bernd Gutte, quien diseñó una versión reducida de un catalizador conocido, la ribonucleasa bovina, y estructuras terciarias que consisten en láminas beta y hélices alfa, incluido un aglutinante de DDT . Urry y sus colegas diseñaron más tarde péptidos fibrosos similares a la elastina basándose en reglas sobre la composición de la secuencia. Richardson y sus colaboradores diseñaron una proteína de 79 residuos sin homología de secuencia con una proteína conocida. ^[2] En la década de 1990, la llegada de potentes computadoras, bibliotecas de conformaciones de aminoácidos y campos de fuerza desarrollados principalmente para simulaciones de dinámica molecular permitieron el desarrollo de herramientas de diseño computacional de proteínas basadas en la estructura. Tras el desarrollo de estas herramientas computacionales, se ha logrado un gran éxito en los últimos 30 años en el diseño de proteínas. La primera proteína diseñada con éxito completamente de novo fue realizada por Stephen Mayo y colaboradores en 1997, ^[3] y, poco después, en 1999 Peter S. Kim y colaboradores diseñaron dímeros, trímeros y tetrámeros de espirales enrolladas dextrógiras no naturales . ^{[4] [5]} En 2003, el laboratorio de David Baker diseñó una proteína completa con un pliegue nunca antes visto en la naturaleza. ^[6] Más tarde, en 2008, el grupo de Baker diseñó computacionalmente enzimas para dos reacciones diferentes. ^[7] En 2010, uno de los anticuerpos ampliamente neutralizantes más poderosos se aisló del suero del paciente utilizando una sonda de proteína diseñada computacionalmente. ^[8] Debido a estos y otros éxitos (por ejemplo, vea los ejemplos a continuación), el diseño de proteínas se ha convertido en una de las herramientas más importantes disponibles para la ingeniería de proteínas . Existe una gran esperanza de que el diseño de nuevas proteínas, pequeñas y grandes, tenga usos en biomedicina y bioingeniería .

Modelos subyacentes de la estructura y función de las proteínas

Los programas de diseño de proteínas utilizan modelos informáticos de las fuerzas moleculares que impulsan a las proteínas en entornos in vivo . Para que el problema sea abordable, estas fuerzas se simplifican mediante modelos de diseño de proteínas. Aunque los programas de diseño de proteínas varían mucho, deben abordar cuatro cuestiones de modelado principales: cuál es la estructura objetivo del diseño, qué flexibilidad se permite en la estructura objetivo, qué secuencias se incluyen en la búsqueda y qué campo de fuerza se utilizará para puntuar las secuencias y las estructuras.

Estructura del objetivo

La proteína Top7 fue una de las primeras proteínas diseñadas para un pliegue que nunca antes se había visto en la naturaleza ^[6]

La función de las proteínas depende en gran medida de su estructura, y el diseño racional de proteínas utiliza esta relación para diseñar la función mediante el diseño de proteínas que tienen una estructura o un pliegue objetivo. Por lo tanto, por definición, en el diseño racional de proteínas la estructura o el conjunto de estructuras objetivo deben conocerse de antemano. Esto contrasta con otras formas de ingeniería de proteínas, como la evolución dirigida , donde se utilizan diversos métodos para encontrar proteínas que logren una función específica, y con la predicción de la estructura de proteínas , donde se conoce la secuencia, pero se desconoce la estructura.

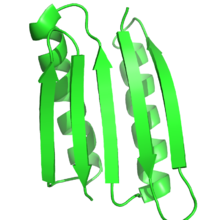
La mayoría de las veces, la estructura objetivo se basa en una estructura conocida de otra proteína. Sin embargo, cada vez es más posible crear nuevos pliegues que no se ven en la naturaleza. Peter S. Kim y sus colaboradores diseñaron trímeros y tetrámeros de espirales superpuestas no naturales, que no se habían visto antes en la naturaleza. ^{[4] [5]} La proteína Top7, desarrollada en el laboratorio de David Baker , se diseñó completamente utilizando algoritmos de diseño de proteínas, hasta obtener un pliegue completamente nuevo. ^[6] Más recientemente, Baker y sus colaboradores desarrollaron una serie de principios para diseñar estructuras de proteínas globulares ideales basadas en embudos de plegamiento de proteínas que sirven de puente entre la predicción de la estructura secundaria y las estructuras terciarias. Estos principios, que se basan tanto en la predicción de la estructura de proteínas como en el diseño de proteínas, se utilizaron para diseñar cinco topologías de proteínas novedosas diferentes. ^[9]

Espacio de secuencia

FSD-1 (mostrado en azul, PDB id: 1FSV) fue el primer diseño computacional de novo de una proteína completa. ^[3] El pliegue objetivo fue el del dedo de zinc en los residuos 33-60 de la estructura de la proteína Zif268 (mostrado en rojo, PDB id: 1ZAA). La secuencia diseñada tenía muy poca identidad de secuencia con cualquier secuencia de proteína conocida.

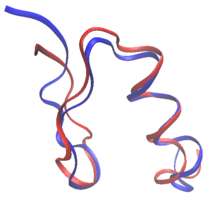
En el diseño racional de proteínas, las proteínas pueden rediseñarse a partir de la secuencia y la estructura de una proteína conocida, o completamente desde cero en el diseño de proteínas de novo . En el rediseño de proteínas, la mayoría de los residuos de la secuencia se mantienen como su aminoácido de tipo salvaje, mientras que se permite que unos pocos muten. En el diseño de novo , se diseña de nuevo toda la secuencia, sin basarse en ninguna secuencia anterior.

Tanto los diseños de novo como los rediseños de proteínas pueden establecer reglas sobre el espacio de secuencias : los aminoácidos específicos que se permiten en cada posición de residuo mutable. Por ejemplo, la composición de la superficie de la sonda RSC3 para seleccionar anticuerpos ampliamente neutralizantes del VIH se restringió en función de los datos evolutivos y el equilibrio de carga. Muchos de los primeros intentos de diseño de proteínas se basaron en gran medida en reglas empíricas sobre el espacio de secuencias. ^[2] Además, el diseño de proteínas fibrosas suele seguir reglas estrictas sobre el espacio de secuencias. Las proteínas diseñadas a base de colágeno , por ejemplo, a menudo están compuestas de patrones repetidos de Gly-Pro-X. ^[2] La llegada de técnicas computacionales permite diseñar proteínas sin intervención humana en la selección de secuencias. ^[3]

Flexibilidad estructural

Los programas de diseño de proteínas más comunes utilizan bibliotecas de rotámeros para simplificar el espacio conformacional de las cadenas laterales de las proteínas. Esta animación recorre todos los rotámeros del aminoácido isoleucina basándose en la penúltima biblioteca de rotámeros (7 rotámeros en total). ^[10]

En el diseño de proteínas, se conocen la estructura (o estructuras) objetivo de la proteína. Sin embargo, un enfoque de diseño de proteínas racional debe modelar cierta flexibilidad en la estructura objetivo para aumentar la cantidad de secuencias que se pueden diseñar para esa estructura y minimizar la posibilidad de que una secuencia se pliegue a una estructura diferente. Por ejemplo, en un rediseño de proteínas de un aminoácido pequeño (como la alanina) en el núcleo fuertemente empaquetado de una proteína, se predeciría que muy pocos mutantes se plegarían a la estructura objetivo mediante un enfoque de diseño racional, si no se permite que las cadenas laterales circundantes se vuelvan a empaquetar.

Por lo tanto, un parámetro esencial de cualquier proceso de diseño es la cantidad de flexibilidad permitida tanto para las cadenas laterales como para la estructura principal. En los modelos más simples, la estructura principal de la proteína se mantiene rígida mientras que algunas de las cadenas laterales de la proteína pueden cambiar de conformaciones. Sin embargo, las cadenas laterales pueden tener muchos grados de libertad en sus longitudes de enlace, ángulos de enlace y ángulos diedros χ . Para simplificar este espacio, los métodos de diseño de proteínas utilizan bibliotecas de rotámeros que asumen valores ideales para las longitudes de enlace y los ángulos de enlace, mientras que restringen los ángulos diedros χ a unas pocas conformaciones de baja energía observadas con frecuencia, denominadas rotámeros .

Las bibliotecas de rotámeros se derivan del análisis estadístico de muchas estructuras proteínicas. Las bibliotecas de rotámeros independientes de la estructura principal describen todos los rotámeros. ^[10] Las bibliotecas de rotámeros dependientes de la estructura principal , por el contrario, describen los rotámeros según la probabilidad de que aparezcan dependiendo de la disposición de la estructura principal de la proteína alrededor de la cadena lateral. ^[11] La mayoría de los programas de diseño de proteínas utilizan una conformación (por ejemplo, el valor modal para los diedros de rotámeros en el espacio) o varios puntos en la región descrita por el rotámero; el programa de diseño de proteínas OSPREY, por el contrario, modela toda la región continua. ^[12]

Aunque el diseño racional de proteínas debe preservar el pliegue general de la estructura principal de una proteína, permitir cierta flexibilidad de la estructura principal puede aumentar significativamente la cantidad de secuencias que se pliegan en la estructura mientras se mantiene el pliegue general de la proteína. ^[13] La flexibilidad de la estructura principal es especialmente importante en el rediseño de proteínas porque las mutaciones de secuencia a menudo resultan en pequeños cambios en la estructura principal. Además, la flexibilidad de la estructura principal puede ser esencial para aplicaciones más avanzadas de diseño de proteínas, como la predicción de enlaces y el diseño de enzimas. Algunos modelos de flexibilidad de la estructura principal del diseño de proteínas incluyen movimientos globales pequeños y continuos de la estructura principal, muestras discretas de la estructura principal alrededor del pliegue objetivo, movimientos de frotamiento hacia atrás y flexibilidad de bucle de proteína. ^{[13] [14]}

Función energética

Comparación de varias funciones de energía potencial. Las más precisas son las que utilizan cálculos mecánicos cuánticos, pero son demasiado lentas para el diseño de proteínas. En el otro extremo, las funciones de energía heurísticas se basan en términos estadísticos y son muy rápidas. En el medio están las funciones de energía de mecánica molecular que tienen una base física pero no son tan costosas computacionalmente como las simulaciones mecánico-cuánticas. ^[15]

Las técnicas de diseño de proteínas racionales deben ser capaces de discriminar entre secuencias que serán estables en el plegamiento objetivo y aquellas que preferirían otros estados competitivos de baja energía. Por lo tanto, el diseño de proteínas requiere funciones de energía precisas que puedan clasificar y puntuar las secuencias en función de lo bien que se pliegan a la estructura objetivo. Al mismo tiempo, sin embargo, estas funciones de energía deben tener en cuenta los desafíos computacionales detrás del diseño de proteínas. Uno de los requisitos más desafiantes para un diseño exitoso es una función de energía que sea precisa y simple para los cálculos computacionales.

Las funciones de energía más precisas son las basadas en simulaciones de mecánica cuántica. Sin embargo, estas simulaciones son demasiado lentas y, por lo general, poco prácticas para el diseño de proteínas. En cambio, muchos algoritmos de diseño de proteínas utilizan funciones de energía basadas en la física adaptadas de programas de simulación de mecánica molecular , funciones de energía basadas en el conocimiento o una combinación híbrida de ambas. La tendencia ha sido hacia el uso de más funciones de energía potencial basadas en la física. ^[15]

Las funciones de energía basadas en la física, como AMBER y CHARMM , generalmente se derivan de simulaciones mecánicas cuánticas y datos experimentales de termodinámica, cristalografía y espectroscopia. ^[16] Estas funciones de energía generalmente simplifican la función de energía física y las hacen descomponibles por pares, lo que significa que la energía total de una conformación de proteína se puede calcular sumando la energía por pares entre cada par de átomos, lo que las hace atractivas para los algoritmos de optimización. Las funciones de energía basadas en la física generalmente modelan un término de Lennard-Jones atractivo-repulsivo entre átomos y un término coulombiano electrostático por pares ^[17] entre átomos no enlazados.

Los enlaces de hidrógeno mediados por agua desempeñan un papel fundamental en la unión proteína-proteína. Una de estas interacciones se muestra entre los residuos D457, S365 en la cadena pesada del anticuerpo ampliamente neutralizante del VIH VRC01 (verde) y los residuos N58 e Y59 en la proteína de la envoltura del VIH GP120 (violeta). ^[18]

Los potenciales estadísticos, a diferencia de los potenciales basados ​​en la física, tienen la ventaja de ser rápidos de calcular, de tener en cuenta implícitamente efectos complejos y de ser menos sensibles a pequeños cambios en la estructura de la proteína. ^[19] Estas funciones de energía se basan en la derivación de valores de energía a partir de la frecuencia de aparición en una base de datos estructural.

Sin embargo, el diseño de proteínas tiene requisitos que a veces pueden ser limitados en los campos de fuerza de la mecánica molecular. Los campos de fuerza de la mecánica molecular, que se han utilizado principalmente en simulaciones de dinámica molecular, están optimizados para la simulación de secuencias individuales, pero el diseño de proteínas busca en muchas conformaciones de muchas secuencias. Por lo tanto, los campos de fuerza de la mecánica molecular deben adaptarse al diseño de proteínas. En la práctica, las funciones de energía de diseño de proteínas a menudo incorporan términos estadísticos y términos basados ​​en la física. Por ejemplo, la función de energía de Rosetta, una de las funciones de energía más utilizadas, incorpora términos de energía basados ​​en la física que se originan en la función de energía CHARMM y términos de energía estadísticos, como la probabilidad de rotámeros y la electrostática basada en el conocimiento. Por lo general, las funciones de energía están altamente personalizadas entre laboratorios y se adaptan específicamente a cada diseño. ^[16]

Desafíos para el diseño eficaz de funciones energéticas

El agua constituye la mayor parte de las moléculas que rodean a las proteínas y es el principal impulsor de su estructura. Por lo tanto, modelar la interacción entre el agua y la proteína es vital en el diseño de proteínas. La cantidad de moléculas de agua que interactúan con una proteína en un momento dado es enorme y cada una de ellas tiene una gran cantidad de grados de libertad y de compañeros de interacción. En cambio, los programas de diseño de proteínas modelan la mayoría de estas moléculas de agua como un continuo, modelando tanto el efecto hidrofóbico como la polarización por solvatación. ^[16]

Las moléculas de agua individuales pueden tener a veces un papel estructural crucial en el núcleo de las proteínas y en las interacciones proteína-proteína o proteína-ligando. Si no se modelan estas aguas, pueden producirse predicciones erróneas de la secuencia óptima de una interfaz proteína-proteína. Como alternativa, se pueden añadir moléculas de agua a los rotámeros. ^[16]

Como un problema de optimización

Esta animación ilustra la complejidad de una búsqueda de diseño de proteínas, que normalmente compara todas las conformaciones de rotámeros de todas las mutaciones posibles en todos los residuos. En este ejemplo, se permite que los residuos Phe36 e His 106 muten a, respectivamente, los aminoácidos Tyr y Asn. Phe y Tyr tienen 4 rotámeros cada uno en la biblioteca de rotámeros, mientras que Asn y His tienen 7 y 8 rotámeros, respectivamente, en la biblioteca de rotámeros (de la penúltima biblioteca de rotámeros de Richardson ^[10] ). La animación recorre todas las (4 + 4) x (7 + 8) = 120 posibilidades. La estructura mostrada es la de la mioglobina, PDB id: 1mbn.

El objetivo del diseño de proteínas es encontrar una secuencia de proteínas que se pliegue hasta una estructura objetivo. Por lo tanto, un algoritmo de diseño de proteínas debe buscar todas las conformaciones de cada secuencia, con respecto al pliegue objetivo, y clasificar las secuencias según la conformación de menor energía de cada una, según lo determina la función de energía de diseño de proteínas. Por lo tanto, una entrada típica para el algoritmo de diseño de proteínas es el pliegue objetivo, el espacio de secuencias, la flexibilidad estructural y la función de energía, mientras que la salida es una o más secuencias que se prevé que se plieguen de manera estable hasta la estructura objetivo.

Sin embargo, el número de secuencias de proteínas candidatas crece exponencialmente con el número de residuos proteicos; por ejemplo, hay 20 ¹⁰⁰ secuencias de proteínas de longitud 100. Además, incluso si las conformaciones de la cadena lateral de aminoácidos se limitan a unos pocos rotámeros (véase Flexibilidad estructural), esto da como resultado un número exponencial de conformaciones para cada secuencia. Por lo tanto, en nuestra proteína de 100 residuos, y suponiendo que cada aminoácido tiene exactamente 10 rotámeros, un algoritmo de búsqueda que busque en este espacio tendrá que buscar en más de 200 ¹⁰⁰ conformaciones proteicas.

Las funciones de energía más comunes se pueden descomponer en términos por pares entre rotámeros y tipos de aminoácidos, lo que convierte el problema en uno combinatorio, y se pueden utilizar potentes algoritmos de optimización para resolverlo. En esos casos, la energía total de cada conformación perteneciente a cada secuencia se puede formular como una suma de términos individuales y por pares entre posiciones de residuos. Si un diseñador solo está interesado en la mejor secuencia, el algoritmo de diseño de proteínas solo requiere la conformación de menor energía de la secuencia de menor energía. En estos casos, se puede ignorar la identidad de aminoácidos de cada rotámero y todos los rotámeros pertenecientes a diferentes aminoácidos se pueden tratar de la misma manera. Sea r _i un rotámero en la posición de residuo i en la cadena de proteína, y E( r _i ) la energía potencial entre los átomos internos del rotámero. Sea E ( r _i , r _j ) la energía potencial entre r _i y el rotámero r _j en la posición de residuo j . Luego, definimos el problema de optimización como uno de encontrar la conformación de energía mínima ( E _T ):

El problema de minimizar E _T es un problema NP-difícil . ^{[14] [20] [21]} Aunque la clase de problemas es NP-difícil, en la práctica muchos casos de diseño de proteínas se pueden resolver de manera exacta u optimizar satisfactoriamente mediante métodos heurísticos.

Algoritmos

Se han desarrollado varios algoritmos específicamente para el problema del diseño de proteínas. Estos algoritmos se pueden dividir en dos grandes clases: algoritmos exactos, como la eliminación de callejones sin salida , que carecen de garantías de tiempo de ejecución pero garantizan la calidad de la solución; y algoritmos heurísticos , como Monte Carlo, que son más rápidos que los algoritmos exactos pero no tienen garantías sobre la optimalidad de los resultados. Los algoritmos exactos garantizan que el proceso de optimización produjo el óptimo de acuerdo con el modelo de diseño de proteínas. Por lo tanto, si las predicciones de los algoritmos exactos fallan cuando estos se validan experimentalmente, entonces la fuente de error puede atribuirse a la función de energía, la flexibilidad permitida, el espacio de secuencia o la estructura objetivo (por ejemplo, si no se puede diseñar para). ^[22]

A continuación se enumeran algunos algoritmos de diseño de proteínas. Aunque estos algoritmos abordan solo la formulación más básica del problema de diseño de proteínas, la ecuación ( 1 ), cuando el objetivo de optimización cambia porque los diseñadores introducen mejoras y extensiones al modelo de diseño de proteínas, como mejoras en la flexibilidad estructural permitida (por ejemplo, flexibilidad de la cadena principal de la proteína) o la inclusión de términos de energía sofisticados, muchas de las extensiones del diseño de proteínas que mejoran el modelado se construyen sobre estos algoritmos. Por ejemplo, Rosetta Design incorpora términos de energía sofisticados y flexibilidad de la cadena principal utilizando Monte Carlo como algoritmo de optimización subyacente. Los algoritmos de OSPREY se basan en el algoritmo de eliminación de callejones sin salida y A* para incorporar movimientos continuos de la cadena principal y de la cadena lateral. Por lo tanto, estos algoritmos proporcionan una buena perspectiva sobre los diferentes tipos de algoritmos disponibles para el diseño de proteínas.

En 2020, los científicos informaron sobre el desarrollo de un proceso basado en IA que utiliza bases de datos genómicas para el diseño basado en la evolución de nuevas proteínas. Utilizaron el aprendizaje profundo para identificar reglas de diseño. ^{[23] [24]} En 2022, un estudio informó sobre un software de aprendizaje profundo que puede diseñar proteínas que contienen sitios funcionales preespecificados. ^{[25] [26]}

Con garantías matemáticas

Eliminación sin salida

El algoritmo de eliminación de extremos muertos (DEE) reduce el espacio de búsqueda del problema de manera iterativa al eliminar rotámeros que se puede demostrar que no forman parte de la conformación global de energía más baja (GMEC). En cada iteración, el algoritmo de eliminación de extremos muertos compara todos los pares posibles de rotámeros en cada posición de residuo y elimina cada rotámero r′ _i que se pueda demostrar que siempre tiene una energía más alta que otro rotámero r _i y, por lo tanto, no forma parte de la GMEC:

${\displaystyle E(r_{i}^{\prime })+\sum _{j\neq i}\min _{r_{j}}E(r_{i}^{\prime },r_{j})>E(r_{i})+\sum _{j\neq i}\max _{r_{j}}E(r_{i},r_{j})}$

Otras extensiones potentes del algoritmo de eliminación de callejones sin salida incluyen el criterio de eliminación de pares y el criterio de eliminación de callejones sin salida generalizado . Este algoritmo también se ha ampliado para manejar rotámeros continuos con garantías demostrables.

Aunque el algoritmo de eliminación de callejones sin salida se ejecuta en tiempo polinomial en cada iteración, no puede garantizar la convergencia. Si, después de una cierta cantidad de iteraciones, el algoritmo de eliminación de callejones sin salida no elimina más rotámeros, entonces se deben fusionar los rotámeros o se debe utilizar otro algoritmo de búsqueda para buscar en el espacio de búsqueda restante. En tales casos, la eliminación de callejones sin salida actúa como un algoritmo de prefiltrado para reducir el espacio de búsqueda, mientras que otros algoritmos, como A*, Monte Carlo, Programación Lineal o FASTER, se utilizan para buscar en el espacio de búsqueda restante. ^[14]

Rama y límite

El espacio conformacional del diseño de proteínas se puede representar como un árbol , donde los residuos de proteínas se ordenan de manera arbitraria y el árbol se ramifica en cada uno de los rotámeros de un residuo. Los algoritmos de ramificación y acotación utilizan esta representación para explorar de manera eficiente el árbol de conformación: en cada ramificación , los algoritmos de ramificación y acotación acotan el espacio conformacional y exploran solo las ramas prometedoras. ^{[14] [27] [28]}

Un algoritmo de búsqueda popular para el diseño de proteínas es el algoritmo de búsqueda A* . ^{[14] [28]} A* calcula una puntuación de límite inferior en cada ruta de árbol parcial que limita (con garantías) la energía de cada uno de los rotámeros expandidos. Cada conformación parcial se agrega a una cola de prioridad y en cada iteración, la ruta parcial con el límite inferior más bajo se extrae de la cola y se expande. El algoritmo se detiene una vez que se ha enumerado una conformación completa y garantiza que la conformación sea la óptima.

La puntuación A* f en el diseño de proteínas consta de dos partes, f=g+h . g es la energía exacta de los rotámeros que ya se han asignado en la conformación parcial. h es un límite inferior de la energía de los rotámeros que aún no se han asignado. Cada uno está diseñado de la siguiente manera, donde d es el índice del último residuo asignado en la conformación parcial.

${\displaystyle g=\sum _{i=1}^{d}(E(r_{i})+\sum _{j=i+1}^{d}E(r_{i},r_{j}))}$

${\displaystyle h=\sum _{j=d+1}^{n}[\min _{r_{j}}(E(r_{j})+\sum _{i=1}^{d}E(r_{i},r_{j})+\sum _{k=j+1}^{n}\min _{r_{k}}E(r_{j},r_{k}))]}$

Programación lineal entera

El problema de optimizar E _T (ecuación ( 1 )) se puede formular fácilmente como un programa lineal entero (ILP). ^[29] Una de las formulaciones más poderosas utiliza variables binarias para representar la presencia de un rotámero y aristas en la solución final, y restringe la solución para tener exactamente un rotámero para cada residuo y una interacción por pares para cada par de residuos:

${\displaystyle \ \min \sum _{i}\sum _{r_{i}}E_{i}(r_{i})q_{i}(r_{i})+\sum _{j\neq i}\sum _{r_{j}}E_{ij}(r_{i},r_{j})q_{ij}(r_{i},r_{j})\,}$

calle

${\displaystyle \sum _{r_{i}}q_{i}(r_{i})=1,\ \forall i}$

${\displaystyle \sum _{r_{j}}q_{ij}(r_{i},r_{j})=q_{i}(r_{i}),\forall i,r_{i},j}$

${\displaystyle q_{i},q_{ij}\in \{0,1\}}$

Los solucionadores ILP, como CPLEX , pueden calcular la solución óptima exacta para grandes instancias de problemas de diseño de proteínas. Estos solucionadores utilizan una relajación de programación lineal del problema, donde q _i y q _ij pueden tomar valores continuos, en combinación con un algoritmo de ramificación y corte para buscar solo una pequeña porción del espacio de conformación para la solución óptima. Se ha demostrado que los solucionadores ILP resuelven muchas instancias del problema de colocación de cadenas laterales. ^[29]

Aproximaciones basadas en el paso de mensajes a la programación lineal dual

Los solucionadores de ILP dependen de algoritmos de programación lineal (LP), como los métodos Simplex o basados ​​en barreras para realizar la relajación de LP en cada rama. Estos algoritmos de LP se desarrollaron como métodos de optimización de propósito general y no están optimizados para el problema de diseño de proteínas (Ecuación ( 1 )). En consecuencia, la relajación de LP se convierte en el cuello de botella de los solucionadores de ILP cuando el tamaño del problema es grande. ^[30] Recientemente, se han diseñado varias alternativas basadas en algoritmos de paso de mensajes específicamente para la optimización de la relajación de LP del problema de diseño de proteínas. Estos algoritmos pueden aproximar tanto las instancias duales como las primarias de la programación entera, pero para mantener garantías de optimalidad, son más útiles cuando se utilizan para aproximar el dual del problema de diseño de proteínas, porque aproximar el dual garantiza que no se pierda ninguna solución. Las aproximaciones basadas en paso de mensajes incluyen el algoritmo de paso de mensajes de producto máximo reponderado en árbol , ^{[31] [32]} y el algoritmo de programación lineal de paso de mensajes . ^[33]

Algoritmos de optimización sin garantías

Monte Carlo y recocido simulado

El algoritmo de Monte Carlo es uno de los más utilizados para el diseño de proteínas. En su forma más simple, el algoritmo de Monte Carlo selecciona un residuo al azar y en ese residuo se evalúa un rotámero elegido al azar (de cualquier aminoácido). ^[21] La nueva energía de la proteína, Enew _, se compara con la energía anterior, Eold _, y el nuevo rotámero se acepta con una probabilidad de:

${\displaystyle p=e^{-\beta (E_{\text{new}}-E_{\text{old}}))},}$

donde β es la constante de Boltzmann y la temperatura T puede elegirse de manera que en las rondas iniciales sea alta y se recozca lentamente para superar los mínimos locales. ^[12]

MÁS RÁPIDO

El algoritmo FASTER utiliza una combinación de criterios deterministas y estocásticos para optimizar las secuencias de aminoácidos. FASTER primero utiliza DEE para eliminar rotámeros que no forman parte de la solución óptima. Luego, una serie de pasos iterativos optimizan la asignación de rotámeros. ^{[34] [35]}

Propagación de creencias

En la propagación de creencias para el diseño de proteínas, el algoritmo intercambia mensajes que describen la creencia que tiene cada residuo sobre la probabilidad de cada rotámero en los residuos vecinos. El algoritmo actualiza los mensajes en cada iteración e itera hasta la convergencia o hasta un número fijo de iteraciones. La convergencia no está garantizada en el diseño de proteínas. El mensaje m _{i→ j} (r _j que un residuo i envía a cada rotámero (r _j en el residuo vecino j se define como:

${\displaystyle m_{i\to j}(r_{j})=\max _{r_{i}}{\Big (}e^{\frac {-E_{i}(r_{i})-E_{ij}(r_{i},r_{j})}{T}}{\Big )}\prod _{k\in N(i)\backslash j}m_{k\to i(r_{i})}}$

Se han utilizado tanto la propagación de creencias de producto máximo como de producto suma para optimizar el diseño de proteínas.

Aplicaciones y ejemplos de proteínas diseñadas

Diseño de enzimas

El diseño de nuevas enzimas es un uso del diseño de proteínas con enormes aplicaciones en bioingeniería y biomedicina. En general, el diseño de una estructura proteica puede ser diferente al diseño de una enzima, porque el diseño de enzimas debe considerar muchos estados involucrados en el mecanismo catalítico . Sin embargo, el diseño de proteínas es un prerrequisito del diseño de enzimas de novo porque, como mínimo, el diseño de catalizadores requiere un andamiaje en el que se pueda insertar el mecanismo catalítico. ^[36]

En la primera década del siglo XXI se lograron grandes avances en el diseño y rediseño de enzimas de novo . En tres estudios importantes, David Baker y colaboradores diseñaron de novo enzimas para la reacción retroaldólica , ^[37] una reacción de eliminación de Kemp, ^[38] y para la reacción de Diels-Alder . ^[39] Además, Stephen Mayo y colaboradores desarrollaron un método iterativo para diseñar la enzima más eficiente conocida para la reacción de eliminación de Kemp. ^[40] Además, en el laboratorio de Bruce Donald , se utilizó el diseño computacional de proteínas para cambiar la especificidad de uno de los dominios proteicos de la sintetasa de péptidos no ribosómicos que produce gramicidina S , de su sustrato natural fenilalanina a otros sustratos no afines que incluyen aminoácidos cargados; las enzimas rediseñadas tenían actividades cercanas a las del tipo salvaje. ^[41]

Diseño semirracional

El diseño semirracional es un método de modificación intencional basado en una cierta comprensión de la secuencia, la estructura y el mecanismo catalítico de las enzimas. Este método se encuentra entre el diseño irracional y el diseño racional. Utiliza información y medios conocidos para realizar modificaciones evolutivas en las funciones específicas de la enzima objetivo. La característica del diseño semirracional es que no se basa únicamente en la mutación aleatoria y el cribado, sino que combina el concepto de evolución dirigida. Crea una biblioteca de mutantes aleatorios con diversas secuencias a través de mutagénesis , RCR propenso a errores , recombinación de ADN y mutagénesis de saturación de sitio . Al mismo tiempo, utiliza la comprensión de las enzimas y los principios de diseño para descartar deliberadamente mutantes con características deseadas.

La metodología del diseño semirracional enfatiza la comprensión profunda de las enzimas y el control del proceso evolutivo. Permite a los investigadores utilizar la información conocida para guiar el proceso evolutivo, mejorando así la eficiencia y la tasa de éxito. Este método desempeña un papel importante en la modificación de la función de las proteínas porque puede combinar las ventajas del diseño irracional y el diseño racional, y puede explorar el espacio desconocido y utilizar el conocimiento conocido para la modificación dirigida.

El diseño semirracional tiene una amplia gama de aplicaciones, que incluyen, entre otras, la optimización de enzimas, la modificación de dianas farmacológicas, la evolución de biocatalizadores, etc. A través de este método, los investigadores pueden mejorar de manera más efectiva las propiedades funcionales de las proteínas para satisfacer necesidades biotecnológicas o médicas específicas. Aunque este método tiene altos requisitos de información y tecnología y es relativamente difícil de implementar, con el desarrollo de la tecnología informática y la bioinformática, las perspectivas de aplicación del diseño semirracional en la ingeniería de proteínas son cada vez más amplias. ^[42]

Diseño para la afinidad

Las interacciones proteína-proteína están implicadas en la mayoría de los procesos bióticos. Muchas de las enfermedades más difíciles de tratar, como el Alzheimer , muchas formas de cáncer (p. ej., TP53 ) y la infección por el virus de la inmunodeficiencia humana ( VIH ), implican interacciones proteína-proteína. Por lo tanto, para tratar dichas enfermedades, es deseable diseñar terapias proteínicas o similares a proteínas que se unan a uno de los socios de la interacción y, por lo tanto, interrumpan la interacción causante de la enfermedad. Esto requiere diseñar terapias proteínicas para la afinidad hacia su socio.

Las interacciones proteína-proteína se pueden diseñar utilizando algoritmos de diseño de proteínas porque los principios que rigen la estabilidad de las proteínas también rigen la unión proteína-proteína. Sin embargo, el diseño de interacciones proteína-proteína presenta desafíos que no suelen estar presentes en el diseño de proteínas. Uno de los desafíos más importantes es que, en general, las interfaces entre proteínas son más polares que los núcleos proteicos, y la unión implica un equilibrio entre la desolvatación y la formación de enlaces de hidrógeno. ^[43] Para superar este desafío, Bruce Tidor y sus colaboradores desarrollaron un método para mejorar la afinidad de los anticuerpos centrándose en las contribuciones electrostáticas. Encontraron que, para los anticuerpos diseñados en el estudio, la reducción de los costos de desolvatación de los residuos en la interfaz aumentaba la afinidad del par de unión. ^{[43] [44] [45]}

Predicciones vinculantes de puntuación

Las funciones energéticas de diseño de proteínas deben adaptarse para lograr predicciones de enlace porque el enlace implica un equilibrio entre las conformaciones de menor energía de las proteínas libres ( E _P y E _L ) y la conformación de menor energía del complejo unido ( E _PL ):

${\displaystyle \Delta _{G}=E_{PL}-E_{P}-E_{L}}$.

El algoritmo K* aproxima la constante de enlace del algoritmo al incluir la entropía conformacional en el cálculo de energía libre. El algoritmo K* considera solo las conformaciones de menor energía de los complejos libres y enlazados (indicados por los conjuntos P , L y PL ) para aproximar las funciones de partición de cada complejo: ^[14]

${\displaystyle K^{*}={\frac {\sum \limits _{x\in PL}e^{-E(x)/RT}}{\sum \limits _{x\in P}e^{-E(x)/RT}\sum \limits _{x\in L}e^{-E(x)/RT}}}}$

Diseño para la especificidad

El diseño de interacciones proteína-proteína debe ser altamente específico porque las proteínas pueden interactuar con una gran cantidad de proteínas; un diseño exitoso requiere aglutinantes selectivos. Por lo tanto, los algoritmos de diseño de proteínas deben poder distinguir entre la unión en el objetivo (o diseño positivo ) y la unión fuera del objetivo (o diseño negativo ). ^{[2] [43]} Uno de los ejemplos más destacados de diseño para la especificidad es el diseño de péptidos de unión a bZIP específicos por Amy Keating y colaboradores para 19 de las 20 familias de bZIP; 8 de estos péptidos eran específicos para su pareja prevista sobre péptidos competidores. ^{[43] [46] [47]} Además, Anderson y colaboradores también utilizaron el diseño positivo y negativo para predecir mutaciones en el sitio activo de un objetivo farmacológico que conferían resistencia a un nuevo fármaco; el diseño positivo se utilizó para mantener la actividad de tipo salvaje, mientras que el diseño negativo se utilizó para interrumpir la unión del fármaco. ^[48] ​​Un reciente rediseño computacional realizado por Costas Maranas y colaboradores también fue capaz de cambiar experimentalmente la especificidad del cofactor de la xilosa reductasa de Candida boidinii de NADPH a NADH . ^[49]

Rejuvenecimiento proteico

El rejuvenecimiento de proteínas consiste en diseñar la superficie de una proteína mientras se preservan intactas las regiones de pliegue, núcleo y límite de la proteína. El rejuvenecimiento de proteínas es especialmente útil para alterar la unión de una proteína a otras proteínas. Una de las aplicaciones más importantes del rejuvenecimiento de proteínas fue el diseño de la sonda RSC3 para seleccionar anticuerpos ampliamente neutralizantes contra el VIH en el Centro de Investigación de Vacunas del NIH. Primero, se seleccionaron residuos fuera de la interfaz de unión entre la proteína de envoltura del VIH gp120 y el anticuerpo b12 descubierto anteriormente para su diseño. Luego, se seleccionó el espacio de secuencias en función de la información evolutiva, la solubilidad, la similitud con el tipo salvaje y otras consideraciones. Luego se utilizó el software RosettaDesign para encontrar secuencias óptimas en el espacio de secuencias seleccionado. Posteriormente, se utilizó RSC3 para descubrir el anticuerpo ampliamente neutralizante VRC01 en el suero de un individuo no progresivo infectado por VIH a largo plazo. ^[50]

Diseño de proteínas globulares

Las proteínas globulares son proteínas que contienen un núcleo hidrófobo y una superficie hidrófila. Las proteínas globulares a menudo asumen una estructura estable, a diferencia de las proteínas fibrosas , que tienen conformaciones múltiples. La estructura tridimensional de las proteínas globulares es típicamente más fácil de determinar a través de cristalografía de rayos X y resonancia magnética nuclear que las proteínas fibrosas y las proteínas de membrana , lo que hace que las proteínas globulares sean más atractivas para el diseño de proteínas que los otros tipos de proteínas. Los diseños de proteínas más exitosos han involucrado proteínas globulares. Tanto RSD-1 como Top7 fueron diseños de novo de proteínas globulares. Cinco estructuras proteicas más fueron diseñadas, sintetizadas y verificadas en 2012 por el grupo Baker. Estas nuevas proteínas no cumplen ninguna función biótica, pero las estructuras están destinadas a actuar como bloques de construcción que se pueden expandir para incorporar sitios activos funcionales. Las estructuras se encontraron computacionalmente utilizando nuevas heurísticas basadas en el análisis de los bucles de conexión entre partes de la secuencia que especifican estructuras secundarias. ^[51]

Diseño de proteínas de membrana

Se han diseñado con éxito varias proteínas transmembrana, ^[52] junto con muchos otros péptidos y proteínas asociados a la membrana. ^[53] Recientemente, Costas Maranas y sus colaboradores desarrollaron una herramienta automatizada ^[54] para rediseñar el tamaño de poro de la porina de membrana externa tipo F (OmpF) de E. coli a cualquier tamaño sub-nm deseado y los ensamblaron en membranas para realizar una separación precisa a escala angstrom.

Otras aplicaciones

Uno de los usos más deseables para el diseño de proteínas es el de los biosensores , proteínas que detectarán la presencia de compuestos específicos. Algunos intentos en el diseño de biosensores incluyen sensores para moléculas no naturales, como el TNT . ^[55] Más recientemente, Kuhlman y sus colaboradores diseñaron un biosensor del PAK1 . ^[56]

En cierto sentido, el diseño de proteínas es un subconjunto del diseño de baterías . ^{[ se necesita más explicación ]}

Véase también

• Ingeniería de proteínas  – Proceso de bioingeniería
• Software de diseño molecular  : software CAD para ingeniería, modelado y análisis a nivel molecularPáginas que muestran descripciones de wikidata como alternativa
  • Comparación de software para modelado de mecánica molecular
  • Software de predicción de la estructura de proteínas
• Biología sintética  : rama interdisciplinaria de la biología y la ingeniería

Referencias

1. Korendovych, Ivan (19 de marzo de 2018). «Diseño minimalista de catalizadores de péptidos y proteínas». American Chemical Society . Consultado el 22 de marzo de 2018 .
2. Richardson, JS; Richardson, DC (julio de 1989). "El diseño de novo de estructuras proteínicas". Tendencias en ciencias bioquímicas . 14 (7): 304–9. doi :10.1016/0968-0004(89)90070-4. PMID  2672455.
3. Dahiyat, BI; Mayo, SL (3 de octubre de 1997). "Diseño de proteínas de novo: selección de secuencias totalmente automatizada". Science . 278 (5335): 82–7. CiteSeerX 10.1.1.72.7304 . doi :10.1126/science.278.5335.82. PMID  9311930. 
4. Gordon, DB; Marshall, SA; Mayo, SL (agosto de 1999). "Funciones energéticas para el diseño de proteínas". Current Opinion in Structural Biology . 9 (4): 509–13. doi :10.1016/s0959-440x(99)80072-4. PMID  10449371.
5. Harbury, PB; Plecs, JJ; Tidor, B; Alber, T; Kim, PS (20 de noviembre de 1998). "Diseño de proteínas de alta resolución con libertad de estructura". Science . 282 (5393): 1462–7. doi :10.1126/science.282.5393.1462. PMID  9822371.
6. Kuhlman, B; Dantas, G; Ireton, GC; Varani, G; Stoddard, BL; Baker, D (21 de noviembre de 2003). "Diseño de un nuevo plegamiento globular de proteínas con precisión a nivel atómico". Science . 302 (5649): 1364–8. Bibcode :2003Sci...302.1364K. doi :10.1126/science.1089427. PMID  14631033. S2CID  1939390.
7. Sterner, R; Merkl, R; Raushel, FM (mayo de 2008). "Diseño computacional de enzimas". Química y biología . 15 (5): 421–3. doi : 10.1016/j.chembiol.2008.04.007 . PMID  18482694.
8. Wu, X; Yang, ZY; Li, Y; Hogerkorp, CM; Schief, WR; Seaman, MS; Zhou, T; Schmidt, SD; Wu, L; Xu, L; Longo, NS; McKee, K; O'Dell, S; Louder, MK; Wycuff, DL; Feng, Y; Nason, M; Doria-Rose, N; Connors, M; Kwong, PD; Roederer, M; Wyatt, RT; Nabel, GJ ; Mascola, JR (13 de agosto de 2010). "El diseño racional de la envoltura identifica anticuerpos monoclonales humanos ampliamente neutralizantes contra el VIH-1". Science . 329 (5993): 856–61. Bibcode :2010Sci...329..856W. doi :10.1126/science.1187659. Número de modelo : PMID 20616233  . 
9. Höcker, B (8 de noviembre de 2012). "Biología estructural: una caja de herramientas para el diseño de proteínas". Nature . 491 (7423): 204–5. Bibcode :2012Natur.491..204H. doi : 10.1038/491204a . PMID  23135466. S2CID  4426247.
10. Lovell, SC; Word, JM; Richardson, JS; Richardson, DC (15 de agosto de 2000). "La penúltima biblioteca de rotámeros". Proteins . 40 (3): 389–408. CiteSeerX 10.1.1.555.4071 . doi :10.1002/1097-0134(20000815)40:3<389::AID-PROT50>3.0.CO;2-2. PMID  10861930. S2CID  3055173. 
11. Shapovalov, MV; Dunbrack RL, Jr (8 de junio de 2011). "Una biblioteca de rotámeros dependiente de la estructura principal suavizada para proteínas derivadas de estimaciones y regresiones de densidad de núcleo adaptativo". Structure . 19 (6): 844–58. doi :10.1016/j.str.2011.03.019. PMC 3118414 . PMID  21645855. 
12. Samish, I; MacDermaid, CM; Pérez-Aguilar, JM; Saven, JG (2011). "Diseño teórico y computacional de proteínas". Revisión anual de química física . 62 : 129–49. Bibcode :2011ARPC...62..129S. doi :10.1146/annurev-physchem-032210-103509. PMID  21128762.
13. Mandell, DJ; Kortemme, T (agosto de 2009). "Flexibilidad de la estructura básica en el diseño computacional de proteínas" (PDF) . Current Opinion in Biotechnology . 20 (4): 420–8. doi :10.1016/j.copbio.2009.07.006. PMID  19709874.
14. Donald, Bruce R. (2011). Algoritmos en biología molecular estructural . Cambridge, MA: MIT Press.
15. Boas, FE y Harbury, PB (2007). "Funciones de energía potencial para el diseño de proteínas". Current Opinion in Structural Biology . 17 (2): 199–204. doi :10.1016/j.sbi.2007.03.006. PMID  17387014.
16. Boas, FE; Harbury, PB (abril de 2007). "Funciones de energía potencial para el diseño de proteínas". Current Opinion in Structural Biology . 17 (2): 199–204. doi :10.1016/j.sbi.2007.03.006. PMID  17387014.
17. Vizcarra, CL; Mayo, SL (diciembre de 2005). "Electrostática en el diseño computacional de proteínas". Current Opinion in Chemical Biology . 9 (6): 622–6. doi :10.1016/j.cbpa.2005.10.014. PMID  16257567.
18. Zhou, T; Georgiev, I; Wu, X; Yang, ZY; Dai, K; Finzi, A; Kwon, YD; Scheid, JF; Shi, W; Xu, L; Yang, Y; Zhu, J; Nussenzweig, MC; Sodroski, J; Shapiro, L; Nabel, GJ; Mascola, JR; Kwong, PD (13 de agosto de 2010). "Base estructural para la neutralización amplia y potente del VIH-1 por el anticuerpo VRC01". Science . 329 (5993): 811–7. Bibcode :2010Sci...329..811Z. doi :10.1126/science.1192819. PMC 2981354 . PMID  20616231. 
19. Mendes, J; Guerois, R; Serrano, L (agosto de 2002). "Estimación de energía en el diseño de proteínas". Current Opinion in Structural Biology . 12 (4): 441–6. doi :10.1016/s0959-440x(02)00345-7. PMID  12163065.
20. Pierce, NA; Winfree, E (octubre de 2002). "El diseño de proteínas es NP-hard". Ingeniería de proteínas . 15 (10): 779–82. doi : 10.1093/protein/15.10.779 . PMID  12468711.
21. Voigt, CA; Gordon, DB; Mayo, SL (9 de junio de 2000). "Intercambio de precisión por velocidad: una comparación cuantitativa de algoritmos de búsqueda en el diseño de secuencias de proteínas". Journal of Molecular Biology . 299 (3): 789–803. CiteSeerX 10.1.1.138.2023 . doi :10.1006/jmbi.2000.3758. PMID  10835284. 
22. Hong, EJ; Lippow, SM; Tidor, B; Lozano-Pérez, T (septiembre de 2009). "Optimización de rotámeros para el diseño de proteínas mediante estimación de MAP y reducción del tamaño del problema". Journal of Computational Chemistry . 30 (12): 1923–45. doi :10.1002/jcc.21188. PMC 3495010 . PMID  19123203. 
23. "El aprendizaje automático revela una receta para construir proteínas artificiales". phys.org . Consultado el 17 de agosto de 2020 .
24. Russ, William P.; Figliuzzi, Matteo; Stocker, cristiano; Barrat-Charlaix, Pierre; Socolich, Michael; Kast, Peter; Hilvert, Donald; Monasson, Rémi; Cocco, Simona; Peso, Martín; Ranganathan, Rama (2020). "Un modelo basado en la evolución para el diseño de enzimas corismatomutasa". Ciencia . 369 (6502): 440–445. Código Bib : 2020 Ciencia... 369.. 440R. doi : 10.1126/ciencia.aba3304. PMID  32703877. S2CID  220714458.
25. "Biólogos entrenan a la IA para generar medicamentos y vacunas". Centro Médico de la Universidad de Washington-Harborview .
26. Wang, Jue; Lisanza, Sidney; Juergens, David; Tischer, Doug; Watson, Joseph L.; Castro, Karla M.; Ragotte, Robert; Saragovi, Amijai; Milles, Lukas F.; Baek, Minkyung; Anishchenko, Ivan; Yang, Wei; Hicks, Derrick R.; Expòsit, Marc; Schlichthaerle, Thomas; Chun, Jung-Ho; Dauparas, Justas; Bennett, Nathaniel; Wicky, Basile IM; Muenks, Andrew; DiMaio, Frank; Correia, Bruno; Ovchinnikov, Sergey; Baker, David (22 de julio de 2022). "Andamiaje de sitios funcionales de proteínas mediante aprendizaje profundo" (PDF) . Science . 377 (6604): 387–394. Código Bibliográfico :2022Sci...377..387W. doi :10.1126/science.abn2100. ISSN  0036-8075. PMC 9621694. PMID  35862514 . 
27. Gordon, DB; Mayo, SL (15 de septiembre de 1999). "Ramificación y terminación: un algoritmo de optimización combinatoria para el diseño de proteínas". Structure . 7 (9): 1089–98. doi : 10.1016/s0969-2126(99)80176-2 . PMID  10508778.
28. Leach, AR; Lemon, AP (1 de noviembre de 1998). "Explorando el espacio conformacional de las cadenas laterales de proteínas utilizando la eliminación de extremos muertos y el algoritmo A*". Proteins . 33 (2): 227–39. CiteSeerX 10.1.1.133.7986 . doi :10.1002/(sici)1097-0134(19981101)33:2<227::aid-prot7>3.0.co;2-f. PMID  9779790. S2CID  12872539. 
29. Kingsford, CL; Chazelle, B; Singh, M (1 de abril de 2005). "Resolución y análisis de problemas de posicionamiento de cadenas laterales mediante programación lineal y entera". Bioinformática . 21 (7): 1028–36. doi : 10.1093/bioinformatics/bti144 . PMID  15546935.
30. Yanover, Chen; Talya Meltzer; Yair Weiss (2006). "Relajaciones de programación lineal y propagación de creencias: un estudio empírico". Revista de investigación en aprendizaje automático . 7 : 1887–1907.
31. Wainwright, Martin J; Tommi S. Jaakkola; Alan S. Willsky (2005). "Estimación de MAP mediante acuerdo sobre árboles: paso de mensajes y programación lineal". IEEE Transactions on Information Theory . 51 (11): 3697–3717. CiteSeerX 10.1.1.71.9565 . doi :10.1109/tit.2005.856938. S2CID  10007532. 
32. Kolmogorov, Vladimir (28 de octubre de 2006). "Paso de mensajes convergente ponderado por árbol para la minimización de la energía". IEEE Transactions on Pattern Analysis and Machine Intelligence . 28 (10): 1568–1583. doi :10.1109/TPAMI.2006.200. PMID  16986540. S2CID  8616813.
33. Globerson, Amir; Tommi S. Jaakkola (2007). "Reparación del producto máximo: algoritmos convergentes de paso de mensajes para relajaciones LP de MAP". Avances en sistemas de procesamiento de información neuronal .
34. Allen, BD; Mayo, SL (30 de julio de 2006). "Mejoras espectaculares del rendimiento del algoritmo de optimización FASTER". Journal of Computational Chemistry . 27 (10): 1071–5. CiteSeerX 10.1.1.425.5418 . doi :10.1002/jcc.20420. PMID  16685715. S2CID  769053. 
35. Desmet, J; Spriet, J; Lasters, I (1 de julio de 2002). "Topología de cadena lateral rápida y precisa y refinamiento energético (FASTER) como un nuevo método para la optimización de la estructura de proteínas". Proteins . 48 (1): 31–43. doi :10.1002/prot.10131. PMID  12012335. S2CID  21524437.
36. Baker, D (octubre de 2010). "Un camino emocionante pero desafiante por delante para el diseño computacional de enzimas". Protein Science . 19 (10): 1817–9. doi :10.1002/pro.481. PMC 2998717 . PMID  20717908. 
37. Jiang, Lin; Althoff, Eric A.; Clemente, Fernando R.; Doyle, Lindsey; Rothlisberger, Daniela; Zanghellini, Alexandre; Gallaher, Jasmine L.; Betker, Jamie L.; Tanaka, Fujie (2008). "Diseño computacional de novo de enzimas retroaldólicas". Science . 319 (5868): 1387–91. Bibcode :2008Sci...319.1387J. doi :10.1126/science.1152692. PMC 3431203 . PMID  18323453. 
38. Röthlisberger, Daniela; Jersonsky, Olga; Wollacott, Andrew M.; Jiang, Lin; Dechancie, Jason; Apuesto, Jamie; Gallaher, Jasmine L.; Althoff, Eric A.; Zanghellini, Alexandre (2008). "Catalizadores de eliminación de Kemp mediante diseño de enzimas computacionales". Naturaleza . 453 (7192): 190–5. Código Bib :2008Natur.453..190R. doi : 10.1038/naturaleza06879 . PMID  18354394.
39. Siegel, JB; Zanghellini, A; Lovick, HM; Kiss, G; Lambert, AR; St Clair, JL; Gallaher, JL; Hilvert, D; Gelb, MH; Stoddard, BL; Houk, KN; Michael, FE; Baker, D (16 de julio de 2010). "Diseño computacional de un catalizador enzimático para una reacción bimolecular estereoselectiva de Diels-Alder". Science . 329 (5989): 309–13. Bibcode :2010Sci...329..309S. doi :10.1126/science.1190239. PMC 3241958 . PMID  20647463. {{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )
40. Privett, HK; Kiss, G; Lee, TM; Blomberg, R; Chica, RA; Thomas, LM; Hilvert, D; Houk, KN; Mayo, SL (6 de marzo de 2012). "Enfoque iterativo para el diseño computacional de enzimas". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 109 (10): 3790–5. Bibcode :2012PNAS..109.3790P. doi : 10.1073/pnas.1118082108 . PMC 3309769 . PMID  22357762. 
41. Chen, CY; Georgiev, I; Anderson, AC; Donald, BR (10 de marzo de 2009). "Rediseño computacional basado en la estructura de la actividad enzimática". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 106 (10): 3764–9. Bibcode :2009PNAS..106.3764C. doi : 10.1073/pnas.0900266106 . PMC 2645347 . PMID  19228942. 
42. Korendovych, Ivan V. (2018). "Diseño de proteínas racional y semirracional". Ingeniería de proteínas . Métodos en biología molecular (Clifton, NJ). Vol. 1685. págs. 15-23. doi :10.1007/978-1-4939-7366-8_2. ISBN 978-1-4939-7364-4. ISSN  1064-3745. PMC  5912912. PMID  29086301 .
43. Karanicolas, J; Kuhlman, B (agosto de 2009). "Diseño computacional de afinidad y especificidad en interfaces proteína-proteína". Current Opinion in Structural Biology . 19 (4): 458–63. doi :10.1016/j.sbi.2009.07.005. PMC 2882636 . PMID  19646858. 
44. Shoichet, BK (octubre de 2007). "No hay almuerzo de energía gratis". Nature Biotechnology . 25 (10): 1109–10. doi :10.1038/nbt1007-1109. PMID  17921992. S2CID  5527226.
45. Lippow, SM; Wittrup, KD; Tidor, B (octubre de 2007). "Diseño computacional de la mejora de la afinidad de los anticuerpos más allá de la maduración in vivo". Nature Biotechnology . 25 (10): 1171–6. doi :10.1038/nbt1336. PMC 2803018 . PMID  17891135. 
46. Schreiber, G; Keating, AE (febrero de 2011). "Especificidad de unión a proteínas versus promiscuidad". Current Opinion in Structural Biology . 21 (1): 50–61. doi :10.1016/j.sbi.2010.10.002. PMC 3053118 . PMID  21071205. 
47. Grigoryan, G; Reinke, AW; Keating, AE (16 de abril de 2009). "El diseño de la especificidad de la interacción de proteínas proporciona péptidos selectivos de unión a bZIP". Nature . 458 (7240): 859–64. Bibcode :2009Natur.458..859G. doi :10.1038/nature07885. PMC 2748673 . PMID  19370028. 
48. Frey, KM; Georgiev, I; Donald, BR; Anderson, AC (3 de agosto de 2010). "Predicción de mutaciones de resistencia mediante algoritmos de diseño de proteínas". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 107 (31): 13707–12. Bibcode :2010PNAS..10713707F. doi : 10.1073/pnas.1002162107 . PMC 2922245 . PMID  20643959. 
49. Khoury, GA; Fazelinia, H; Chin, JW; Pantazes, RJ; Cirino, PC; Maranas, CD (octubre de 2009). "Diseño computacional de la xilosa reductasa de Candida boidinii para la especificidad del cofactor alterada". Protein Science . 18 (10): 2125–38. doi :10.1002/pro.227. PMC 2786976 . PMID  19693930. 
50. Burton, DR; Weiss, RA (13 de agosto de 2010). "SIDA/VIH. Un impulso para el diseño de vacunas contra el VIH". Science . 329 (5993): 770–3. Bibcode :2010Sci...329..770B. doi :10.1126/science.1194693. PMID  20705840. S2CID  206528638.
51. Jessica Marshall (7 de noviembre de 2012). "Proteínas hechas a medida". Nature News . Consultado el 17 de noviembre de 2012 .
52. Proteínas de horquilla alfa transmembrana diseñadas en la base de datos OPM
53. Péptidos y proteínas asociados a la membrana diseñados en la base de datos OPM
54. Chowdhury, Ratul; Kumar, Manish; Maranas, Costas D.; Golbeck, John H.; Baker, Carol; Prabhakar, Jeevan; Grisewood, Matthew; Decker, Karl; Shankla, Manish (10 de septiembre de 2018). "PoreDesigner para ajustar la selectividad de solutos en un poro de membrana externa robusto y altamente permeable". Nature Communications . 9 (1): 3661. Bibcode :2018NatCo...9.3661C. doi :10.1038/s41467-018-06097-1. ISSN  2041-1723. PMC 6131167 . PMID  30202038. 
55. Looger, Loren L.; Dwyer, Mary A.; Smith, James J. y Hellinga, Homme W. (2003). "Diseño computacional de proteínas receptoras y sensoras con nuevas funciones". Nature . 423 (6936): 185–190. Bibcode :2003Natur.423..185L. doi :10.1038/nature01556. PMID  12736688. S2CID  4387641.
56. Jha, RK; Wu, YI; Zawistowski, JS; MacNevin, C; Hahn, KM; Kuhlman, B (21 de octubre de 2011). "Rediseño del dominio autoinhibitorio de PAK1 para mejorar la estabilidad y la afinidad en aplicaciones de biosensores". Journal of Molecular Biology . 413 (2): 513–22. doi :10.1016/j.jmb.2011.08.022. PMC 3202338 . PMID  21888918. 

Lectura adicional

• Donald, Bruce R. (2011). Algoritmos en biología molecular estructural. Biología molecular computacional. Cambridge, MA: The MIT Press. ISBN 9780262015592.OCLC 1200909148  .
• Jin, Wenzhen; Kambara, Ohki; Sasakawa, Hiroaki; Tamura, Atsuo y Takada, Shoji (mayo de 2003). "Diseño de novo de proteínas plegables con embudo de plegado suave: diseño negativo automatizado y verificación experimental". Structure . 11 (5): 581–590. doi : 10.1016/S0969-2126(03)00075-3 . PMID  12737823.
• Pokala, Navin y Handel, Tracy M. (2005). "Funciones energéticas para el diseño de proteínas: ajuste con afinidades de complejos proteína-proteína, modelos para el estado desplegado y diseño negativo de solubilidad y especificidad". Journal of Molecular Biology . 347 (1): 203–227. doi :10.1016/j.jmb.2004.12.019. PMID  15733929.
• Lijadora, Chris; Amigo, Gerrit; Bazán, Fernando; Horovitz, Amnón; Nakamura, Haruki; Ribas, Luis; Finkelstein, Alexei V.; Lockhart, Andrés; Merkl, Rainer; et al. (febrero de 1992). "Diseño de proteínas en computadoras. Cinco nuevas proteínas: Shpilka, Grendel, Fingerclasp, Leather y Aida". Proteínas: estructura, función y bioinformática . 12 (2): 105-110. doi :10.1002/prot.340120203. PMID  1603799. S2CID  38986245.